СИСТЕМЫ УПРАВЛЕНИЙ
УДК 62.50
М.С. Габриелян, В.Р. Барсегян
О приоритете выбора сигналов в задаче оптимального
наблюдения
(Представлено академиком Ю.Г. Шукуряном 11/XII
2003)
Рассматривается задача оптимального
наблюдения линейных систем при наличии нескольких различных сигналов.
1. Пусть имеется система
|
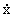 = A(t)x, = A(t)x, | |
(1.1) |
где x О
Rn, A(t) - (n × n) матрицы с измеримыми и
ограниченными элементами на промежутке t О
[t0, T].
Пусть имеется возможность на промежутке
времени [t - J,t], где J > 0, измерять величины
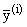 (t) = (t) =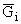 (t)x(t) (i = 1,ј,k), (t)x(t) (i = 1,ј,k), | |
(1.2) |
где
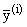 (t) -
(mi × 1)-мерная, а
(t) -
(mi × 1)-мерная, а 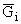 (t) - (mi × n)-мерная матрица, элементы которых
кусочно-непрерывные функции при t О [t - J,t].
Обозначим через m = max{m1,ј,mk}.
(t) - (mi × n)-мерная матрица, элементы которых
кусочно-непрерывные функции при t О [t - J,t].
Обозначим через m = max{m1,ј,mk}.
Сигналы
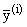 (t) и
матрицы
(t) и
матрицы 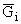 (t) (i = 1,ј,k) дополним
на отрезке t О
[t - J,t] нулями до
размерности (m × n) [1] и обозначим их
соответственно через y(i)(t) и
Gi(t).
(t) (i = 1,ј,k) дополним
на отрезке t О
[t - J,t] нулями до
размерности (m × n) [1] и обозначим их
соответственно через y(i)(t) и
Gi(t).
Пусть ai
О [0,1] (i = 1,ј,k)
независимые параметры. Рассмотрим процесс наблюдения системы (1.1) при сигнале
| y(t, a1,ј,ak) = |
k
е
i=1
|
aiy(i)(t) = |
k
е
i=1
|
aiGi(t)x(t) | |
или
| y(t, a1,ј,ak) = G(t, a1,ј,ak)x(t), где
G(t, a1,ј,ak) = |
k
е
i=1
|
aiGi(t). | |
(1.3) |
Требуется определить оптимальные линейные
операции, удовлетворяющие следующим условиям:
| jj[t, y(t, a1,ј,ak)] = xj(t)
(j = 1,ј,n). | |
Целесообразно указанные линейные операции
искать в следующей матричной форме:
|
t
у
х
t-J
|
V(t, t; ·)y(t, a1,ј,ak)dt = x(t). | |
Здесь матрица V(t, t; ·) имеет размерность (n × m). Формула Коши для решения
системы (1.1) будет
где X[t,t] - нормированная фундаментальная матрица системы (1.1).
Подставляя значение x(t) из (1.4) в (1.3), получим
|
t
у
х
t-J
|
V(t, t; ·)G(t, a1,ј,ak)X[t,t]x(t)dt =
x(t). | |
(1.5) |
Так как вектор x(t) может принимать любое
значение из Rn, то из (1.5) следует, что
|
t
у
х
t-J
|
V(t, t; ·)G(t, a1,ј,ak)X[t,t]dt =
E, | |
(1.6) |
где E единичная матрица.
Матричную функцию V(t, t; ·), удовлетворяющую условию (1.6), можно определить при
помощи проблемы моментов при минимизации соответствующего функционала:
а) при минимизации функционала
|
ж
и |
t
у
х
t-J
|
V2(t, t; ·)dt |
ц
ш |
[1/2]
|
| |
(1.7) |
с условиями (1.6) определение
оптимального фильтра можно привести к изопериметрической задаче [2];
б) при минимизации функционала
|
sup
t-J Ј t Ј
t
|
|
n
е
i=1
|
|
m
е
j=1
|
|Vij(t, t; ·)| | |
с
условиями (1.6) оптимальный фильтр можно определить при помощи проблемы моментов
[2] и т.д.
Таким образом, когда минимизируемый
функционал удовлетворяет условиям нормы, решение первого этапа поставленной
задачи приводится к проблеме моментов.
Решая сформулированные задачи при различных
критериях, получаем минимальную величину нормы фильтра
| r*[j(·; a1,ј,ak)] = f(a1,ј,ak), | |
зависимую
от параметров a1,ј,ak.
Эта величина непрерывно зависит от указанных
параметров. Так как ai О [0,1], то минимум нормы r*[j(·;a1,ј,ak)] по a1,ј,ak достижим.
При норме (1.7) r02 является квадратичной формой,
зависимой от a1,ј,ak. Следует заметить,
что если r0 > 0, а система (1.1) и
сигналы (1.2) стационарные, то получим условие вполне наблюдаемости [2,3].
Замечание. Те
значения параметров системы ai (i = 1,ј,k), при которых норма указанного фильтра неограниченна
(норма сопряженного пространства r0 = 0), не
рассматриваются, так как в этих случаях система не является вполне наблюдаемой.
2. Рассмотрим систему
|
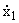 = x2, = x2, 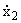 = -x1. = -x1. |
|
(2.1) |
Пусть поступают сигналы
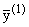 (t) = g1x1(t), (t) = g1x1(t),
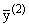 (t) = g2x2(t), (t) = g2x2(t),
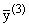 (t) = g11x1(t) + g22x2(t), (t) = g11x1(t) + g22x2(t), | |
где
gi = const, gii = | const, (i = 1,2).
Нормированная фундаментальная матрица системы (2.1) имеет вид
Интегральные условия
(1.6) для данной задачи будут:
|
|
0
у
х
-J
|
(a1cosz - a2sinz)V1(z, ·)dz = 1,
| |
|
0
у
х
-J
|
(a2cosz + a1sinz)V1(z, ·)dz =
0, | |
|
0
у
х
-J
|
(a1cosz - a2sinz)V2(z, ·)dz = 0,
| |
|
0
у
х
-J
|
(a2cosz + a1sinz)V2(z, ·)dz =
1, | | |
| |
(2.2) | где приняты следующие обозначения:
| a1 = a1g1 + a3g11,
a2 = a2g2 + a3g22,
ai О
[0,1] (i = 1,2,3), | |
t - t = z, 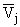 (t, t + z, ·) = Vj(z, ·) (j = 1,2). (t, t + z, ·) = Vj(z, ·) (j = 1,2). |
|
Найдем функции V1(z,·) и V2(z,·),
удовлетворяющие интегральным условиям (2.2) и являющиеся оптимальными в смысле
|
0
у
х
-J
|
[V12(z, ·) + V22(z, ·)]dz ® |
min
|
. | |
(2.3) | Следуя [2], нужно найти числа
l1,l2,l3,l4, связанные условием
которые минимизируют квадрат нормы
основного пространства
| r02 = |
min
l1+l4=1
|
|
0
у
х
-J
|
[h12(z) + h22(z)]dz, | |
(2.5) | где
|
| h1(z) = l1(a1cosz - a2sinz) + l2(a2cosz + a1sinz), | |
| h2(z) = l3(a1cosz - a2sinz) + l4(a2cosz + a1sinz). | | |
| |
(2.6) |
Подставляя (2.6) в (2.5), проведя некоторые
вычисления и применяя метод неопределенных множителей Лагранжа для нахождения
l10, l20, l30 и
l40, получим следующую систему алгебраических уравнений:
|
| (a12s1 + a22s2 - 2a1a2s3)l1 + [a1a2(s1 - s2) + (a12 - a22)s3]l2 = -l, | |
| [a1a2(s1 - s2) + (a12 - a22)s3]l1 + (a22s1 + a12s2 + 2a1a2s3)l2 = 0, | |
| (a12s1 + a22s2 - 2a1a2s3)l3 + [a1a2(s1 - s2) + (a12 - a22)s3]l4 = 0, | |
| [a1a2(s1 - s2) + (a12 - a22)s3]l3 + (a22s1 + a12s2 + 2a1a2s3)l4 = -l, | | |
| |
(2.7) | где s1 = J + [(sin2J)/2], s2 = J - [(sin2J)/2], s3 = -sin2J, l неопределенный множитель.
Решая полученную замкнутую систему (2.7),
(2.4), получим
|
| l10 = |
a22s1 + a12s2 + 2a1a2s3
(s1 + s2)(a12 + a22)
|
,
l20 = l30 =- |
a1a2(s1 - s2) + (a12 - a22)s3
(s1 + s2)(a12 + a22)
|
, | |
| l40 = |
a22s1 + a12s2 - 2a1a2s3
(s1 + s2)(a12 + a22)
|
. | | |
| |
(2.8) | Подставляя (2.8) в (2.6), а затем
в (2.5), получим
| r02(·) = |
1
4
|
(J2 - sin2J)(a12 + a22). | | Искомые
функции Vi0(z,·) будут:
| Vi0(z, ·) = |
1
r02(·)
|
hi0(z)
(i = 1,2), | | где
hi0(z) имеют вид (2.6).
Для нормы (2.3) получим
| ||V0(·)||2= |
1
r02(·)
|
= |
4
(J2 - sin2J)(a12 + a22)
|
. | | Учитывая обозначения
для a1 и a2, получаем
| ||V0(·)||2 = |
1
r02(·)
|
= |
4
(J2 - sin2J)[(a1g1 + a3g11)2 + (a2g2 + a3g22)2]
|
. | | Следовательно,
минимум ||V0(a1,a2,a3,a4)|| будет при максимуме выражения
| F(·) = (a1g1 + a3g11)2 + (a2g2 + a3g22)2. | |
Максимизируя функцию F(a1,a2,a3) при ai
О [0,1] (i = 1,2,3), получим тот сигнал, который в
вышеуказанном смысле является оптимальным.
Для определенности предполагая, что
g1 = g2 = 1, g11 < 0, g22 < 0, F
получит максимальное значение при a1 = a2 = 1.
Ереванский государственный университет
Литература
1. Габриелян М.С., Барсегян В.Р.
- ДНАН Армении. 2002. Т. 102. N3. С.
219-222.
2. Красовский Н.Н.
Теория управления движением. М. Наука. 1968. 476
с.
3. Калман Р.Е. - Труды I конгресса ИФАК. М. АН СССР. 1961. Т. 1. С. 521-547.
|
![]() (t) =
(t) =![]() (t)x(t) (i = 1,ј,k),
(t)x(t) (i = 1,ј,k),![]() (t) -
(mi × 1)-мерная, а
(t) -
(mi × 1)-мерная, а ![]() (t) - (mi × n)-мерная матрица, элементы которых
кусочно-непрерывные функции при t О [t - J,t].
Обозначим через m = max{m1,ј,mk}.
(t) - (mi × n)-мерная матрица, элементы которых
кусочно-непрерывные функции при t О [t - J,t].
Обозначим через m = max{m1,ј,mk}.
![]() (t) и
матрицы
(t) и
матрицы ![]() (t) (i = 1,ј,k) дополним
на отрезке t О
[t - J,t] нулями до
размерности (m × n) [1] и обозначим их
соответственно через y(i)(t) и
Gi(t).
(t) (i = 1,ј,k) дополним
на отрезке t О
[t - J,t] нулями до
размерности (m × n) [1] и обозначим их
соответственно через y(i)(t) и
Gi(t). ![]() = x2,
= x2, ![]() = -x1.
= -x1. ![]() (t) = g1x1(t),
(t) = g1x1(t),
![]() (t) = g2x2(t),
(t) = g2x2(t),
![]() (t) = g11x1(t) + g22x2(t),
(t) = g11x1(t) + g22x2(t),![]() (t, t + z, ·) = Vj(z, ·) (j = 1,2).
(t, t + z, ·) = Vj(z, ·) (j = 1,2).