УДК 517

   Пусть p і 1 и замкнутая в ортогональная система. Предположим, что для каждой функции f(x) Осуществуют числа и , для которых выполняется равенство

(1)

   Отметим, что этот выбор может быть не единственным. Определим последовательности   нелинейных   операторов   {G_m(x, f, j, L^p) и {R_m(x, f, j, L^p) следующим образом:

G0(x, f, j, Lp) = 0,    R0(x, f, j, Lp) = f(x),

G1(x, f, j, Lp) = где иопределяются из (1),

R1(x, f, j, Lp) = f(x) - G1(x, f, j, Lp).

Gm+1(x, f, j, Lp) = Gm(x, f, j, Lp) + G1(x,Rm(x, f, j, Lp),j, Lp),

Rm+1(x, f, j, Lp) = f(x) - Gm+1(x, f, j, Lp).

Заметим, что последовательности {G_m(x, f, j, L^p) и {R_m(x, f, j, L^p) могут определяться неоднозначно. Последовательность нелинейных операторов {G_m(x, f, j, L^p) называется L^p-гриди алгоритмом функции f(x) по системе j. Такой алгоритм для банаховых пространств был расмотрен В. Н. Темляковым [1]. Гриди (жадный) алгоритмы разных типов изучены Р. ДеВором и В. Н. Темляковым [1,2].
   Определение 1. Говорят, что L^p-гриди алгоритм функции f О L^p[0,1] по системе j сходится к ней, если (некоторая) последовательность {G_m(x, f, j, L^p) сходится к f(x) по L^p[0,1] норме, т. е.

lim m®Ґ  ||f - Gm(f, j, Lp)||p = 0.

   В. Н. Темляковым был поставлен вопрос: сходится ли L^p-гриди алгоритм (p > 1) по системе Хаара (см. [1], с. 7, 20)? В настоящей работе доказывается, что этот вопрос при p = 1 имеет отрицательный ответ.
   Напомним определение ортонормированной системы Хаара

c0(0)(x) = c0(x) = 1

ck(m) = м п п н п п о 2[(k-1)/2]        m-1 2k-1 < x < 2m-1 2k , k = 1,2,3,ј -2[(k-1)/2]        2m-1 2k < x < m 2k-1 , 1 Ј m Ј 2k-1 0        для остальных x.

   Для системы Хаара справедлива
   Теорема 1. Для любой функции f О L¹[0,1] существуют числа,и (вообще говоря, не единственные), для которых справедливо равенство

   Следовательно, можно определить L¹-гриди алгоритм по системе Хаара. Следует отметить, что не всякие полные ортогональные системы обладают этим свойством. В частности для полной ортонормированной системы {w_k(x), построенной М. Г. Григоряном [3], для любой функции f О L¹[0,1] имеет место

inf a,k  ||f - awk||1 = 0.

   Определение 2. Пусть f О L¹[t₁,t₂], g О L¹[t₁,t₂]. Если

|| f ||L1[t1,t2] - inf a  || f - ag ||L1[t1,t2] = 0,

то скажем, что функция g не может понизить норму f.
   Пусть

P(x) = м п н п о 1     0 Ј x < 5 8 , 3 4 Ј x < 7 8 , -1     5 8 Ј x < 3 4 , 7 8 Ј x Ј 1.

   Для каждого натурального r обозначим через F_r совокупность всех функций вида

j(x) = м п п п п п н п п п п п о P(2k+1x - 1); 1 2k+1 Ј x < 1 2k     k = r,r + 1,ј 0; 1 2 Ј x Ј 1 g(x); где g(x)  неотрицательная, интегрируемая функция на й к л 1 2r , 1 2 щ ъ ы , с mesE{x;  g(x) = 0,x О [2-1-p,2-p]} і 3 2p+3  p = 1,2,ј, r - 1.

   Верна
   Теорема 2. Для любого r О N и для каждой j О F_r, существуют единственные , иО R такие, что

1)

при этом

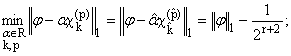
2)  R1(x, j, c, L1) = j(x) -(x) О Fr+1.

   Основным средством для доказательства этой теоремы является
   Лемма 1. Для любого r О N и для каждой j О F_r
1) ни одна функция из системы Хаара с верхним индексом 1 не может понизить норму  j;
2) ни одна функция из системы Хаара с нижним индексом меньше (r + 2) не может понизить норму  j.
   Теорема 3. Существует функция j О L¹[0,1], для которой

||j - Gn(j, c, L1)||1 = ||j||1 - 1 4 n е k=1  2-k.

   Доказательство. В качестве j(x) возьмем j(x) О F₁. Тем самым функция j(x) определяется однозначно (в F₁ содержится одна функция). Согласно теореме 2

R1(x, j, c, L1) = j(x) - c3(2)(x), ||R1(j, c, L1)||1 = ||j||1 - 1 23 .

   Принимая во внимание, что R₁(x, j, c, L¹) О F₂, можем к нему применить теорему 2 при r = 2. n раз применяя теорему 2,

Rn(x, j, c, L1) = Rn-1(x, j, c, L1) -(x) О Fn+1,

||Rn(j, c, L1)||1 = ||Rn-1(j, c, L1)||1 - 1 2n+2 = ј  = ||j||1 - 1 4 n е k=1  2-k,

то есть

||j - Gn(j, c, L1)||1 = ||j||1 - 1 4 n е k=1  2-k.

Теорема 3 доказана.
   Из этой теоремы вытекает
   Теорема 4. Существует функция j О L¹[0,1], L¹-гриди алгоритм которой по системе Хаара расходится.
   В заключение выражаю благодарность профессору М. Г. Григоряну, под руководством которого выполнена эта работа.

     Ереванский государственный университет