Reports-2004-Vol104-N2-Avetisyan

МАТЕМАТИКА

УДК 519.68:510

С. А. Аветисян

О представлении бестиповых l-термов помеченными бинарными
деревьями

(Представлено академиком Н.У. Аракеляном 2/III 2004)

   1. Используемые определения (см. [1, 2]). Зафиксируем счетное множество переменных V. Множество термов L является наименьшим множеством, удовлетворяющим следующим условиям:
   1) если x О V, то x О L;
   2) если t₁,t₂ О L, то (t₁t₂) О L;
   3) если x О V и t О L, то (lxt) О L.
   Введем сокращенную запись термов: терм (ј(t₁t₂)јt_k), где t_i О L, i=1,ј,k, k > 1, условимся обозначать t₁t₂јt_k; терм (lx₁(lx₂(ј(lx_mt)ј), где x_j О V, t О L, условимся обозначать lx₁x₂јx_m.t, j=1,ј,m, m > 0.
   Традиционным образом вводятся понятия свободного и связанного вхождения переменной в терм, понятие свободной переменной терма.
   Через t[x₁,ј,x_m] условимся обозначать терм t с указанием интересующих нас попарно различных переменных x₁,ј,x_m, m і 1. Через t[t₁,ј,t_m] обозначим терм, полученный в результате одновременной подстановки термов t₁,ј,t_m в терм t вместо всех свободных вхождений переменных x₁,ј,x_m соответственно.
   Термы t₁ и t₂ назовем конгруэнтными (обозначим t₁ є t₂), если один терм можно получить из другого переименованием связанных переменных. Далее мы не будем отличать конгруэнтные термы.
   Напомним понятие b-редукции:

b = {((lx.t[x])tў, t[tў])|t, tў О L,x О V}.

Одношаговая b-редукция (®_b) определяется обычным образом. Напомним, что терм (lx.t[x])tў называется b-редексом (далее просто редексом), а терм t[tў] - его сверткой. Терм, не содержащий редексов, называется b-нормальной формой (далее просто нормальной формой). Терм вида lx₁јx_k.xt₁јt_m, где x,x_i О V, t_j О L, i=1,ј,k, j=1,ј,m, k і 0, m і 0, называется головной нормальной формой.

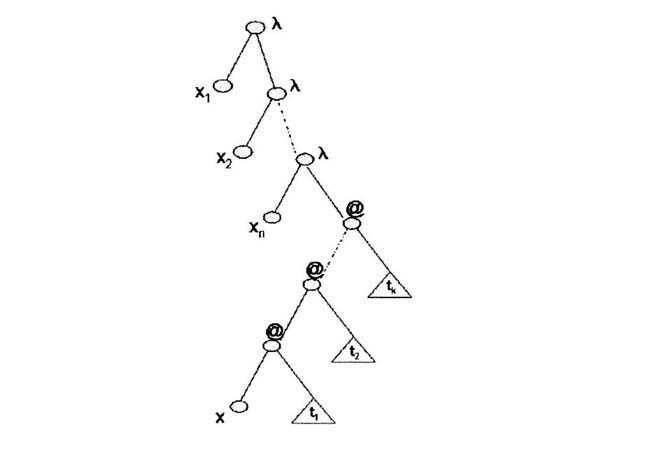
   2. Представление терма. Любой терм t О L можно представить в виде помеченного бинарного дерева, нетерминальные узлы которого представляют собой операции аппликации или абстракции, терминальные узлы (листья) - переменные терма. Под t-деревом будем понимать дерево, соответствующее терму t, которое будем отождествлять с самим термом t. Дадим рекурсивное определение t-дерева.
   - Любой переменной x О V соответствует дерево, состоящее из одного узла. Отметим ее переменной x. Такой узел назовем v-узлом.
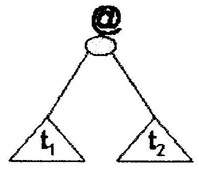
   - Если t₁, t₂ О L, то терму (t₁t₂) соответствует дерево, корень которого помечен символом @. Левое поддерево является t₁-деревом, правое поддерево - t₂-деревом. Корень (t₁t₂)-дерева будем называть @-узлом, t₁-дерево - левым поддеревом @-узла, t₂-дерево - правым поддеревом @-узла. (t₁t₂)-дерево имеет следующий вид:

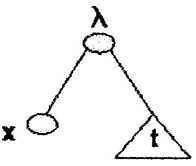
- Если t О L, x О V, то терму (lx.t) соответствует дерево, корень которого помечается символом l и называется l-узлом. Левое поддерево представляется листом, помеченным переменной x. Левое поддерево будем называть переменной l-узла. Правое поддерево является t-деревом. Правое поддерево будем называть телом l-узла. (lx.t)-дерево имеет следующий вид:

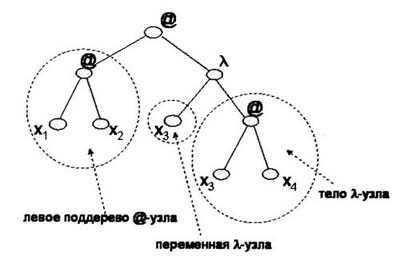
Из определения следует, что t-дерево содержит узлы трех типов: v-узел, @-узел, l-узел. Например, дерево, соответствующее терму ((x₁x₂)(lx₃.x₃x₄)), представлено на рис. 1.
Каждому терму t, а, следовательно, и t-дереву, соответствует множество свободных переменных. В описанном выше примере (рис. 1) переменные x₁, x₂, x₄ являются свободными.

Рис.1. Представление терма ((x₁x₂)(lx₃.x₃x₄)) в виде помеченного бинарного дерева

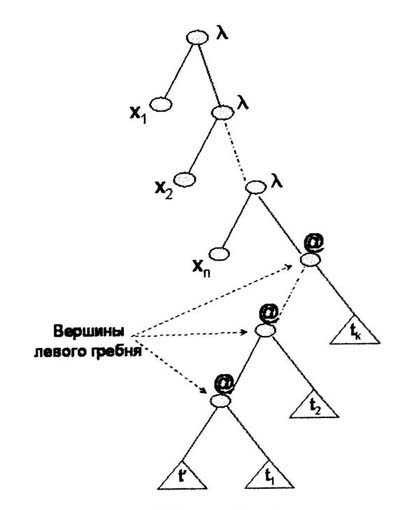
3. Представление головной нормальной формы. Любой терм t имеет следующий вид:

lx₁x₂јx_n.tўt₁t₂јt_k,

где tў - переменная, если k=0, и tў - переменная, либо терм вида lx.tўў, если k > 0, x,x_i О V, i=1,ј,n, tў,tўў,t_j О L, j=1,ј,k, k і 0, n і 0. Соответствующее t-дерево представлено на рис. 2.
Под левым гребнем t-дерева будем понимать путь, состоящий из @-узлов, встречающихся при спуске по левым поддеревьям @-узлов начиная с первого (рис. 2). Если в представлении t-дерева tў представляет собой v-узел, то такому t-дереву (рис. 3) соответствует головная нормальная форма, а соответствующий терм имеет следующий вид:

lx₁x₂јx_n.xt₁t₂јt_k,

где x,x_i О V, t_j О L, i=1,ј,n, j=1,ј,k, k,n і 0.
t-дерево, соответствующее головной нормальной форме, характеризуется v-узлом, которому соответствует переменная головной нормальной формы x, и @-узлами, правые поддеревья которых являются t₁-деревом, t₂-деревом, ..., t_k-деревом соответственно (рис. 3). Описанные @-узлы являются узлами левого гребня t-дерева. Если n=0, то отсутствуют лидирующие (корневые) l-узлы, если k=0, то отсутствуют @-узлы левого гребня t-дерева.

Рис.2. Общий вид t-дерева

Рис.3. t-дерево, соответствующее головной нормальной форме lx₁x₂јx_n.xt₁t₂јt_k.

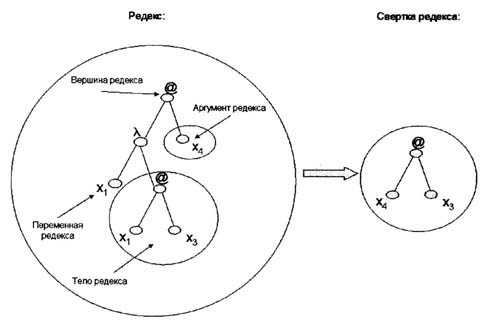
4. Преобразование t-дерева в tў-дерево, соответствующее одношаговой b-редукции. Рассмотрим сначала получение свертки редекса. Редексом является терм (lx.t₁[x])t₂, где t₁ - тело редекса, t₂ - аргумент редекса, x - переменная редекса. Дерево редекса имеет следующий вид:

где t₂-дерево соответствует аргументу редекса, t₁-дерево соответствует телу редекса. Под корнем редекса будем понимать корневую вершину дерева редекса.

    Алгоритм Red1 преобразования дерева редекса в дерево свертки состоит из следующих шагов:
   1) выделить t₂-дерево, соответствующее аргументу редекса;
   2) заменить каждый лист, представляющий свободное вхождение переменной x в t₁-дереве, на t₂-дерево. Преобразованное t₁-дерево соответствует свертке;
   3) за корневую вершину дерева свертки принять корневую вершину преобразованного t₁-дерева;
   4) удалить все не используемые в преобразованном t₁-дереве узлы.

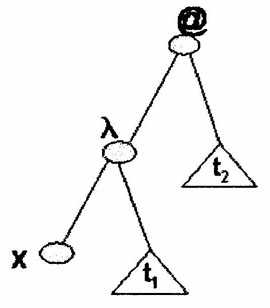
При замене переменной в теле редекса на аргумент редекса свободная переменная аргумента редекса может связаться. При обнаружении связывания осуществляется переименование связанной переменной тела редекса на новую переменную. Пример получения свертки (lx₁.(x₁x₃) )x₄ представлен на рис. 4.

    Алгоритм Red преобразования t-дерева в tў-дерево, согласно одношаговой b-редукции, состоит из следующих шагов:
   1. найти @-узел, который является корнем редекса. Если соответствующий @-узел найден, то отметить его;
   2. рассмотреть tўў-дерево, корнем которого является отмеченный @-узел;
   3. преобразовать tўў-дерево в дерево-свертку согласно алгоритму Red1;
   4. заменить поддерево, корнем которого является отмеченный @-узел, на преобразованное tўў-дерево-свертку.

Рис.4. Преобразование дерева-редекса в дерево-свертку для редекса (lx₁.(x₁ x₃) )x₄.

Утверждение 1. Пусть терм t не является нормальной формой, тогда алгоритм Red переводит t-дерево в tў-дерево так, что t®_b tў.

5. Преобразование t-дерева в tў-дерево, соответствующее подстановке. Пусть t є t[x₁,ј,x_m], где x₁,ј,x_m попарно различные переменные, m і 1. Пусть tў є t[t₁,ј,t_m], где t₁,ј,t_m - термы.

    Алгоритм Sub преобразования t-дерева в tў-дерево, соответствующее подстановке, состоит из следующих шагов:
   1. в t-дереве найти и отметить v-узлы, соответствующие свободным вхождениям переменных x₁,ј,x_m;
   2. заменить каждый отмеченный v-узел, соответствующий свободному вхождению переменной x_i, на t_i-дерево, i=1,ј,m.

Очевидно, что при подстановке возникает проблема связывания свободных переменных. При обнаружении связывания происходит переименование переменных l-узлов. Переименование переменных l-узлов заключается в переименовании всех свободных вхождений данной переменной в теле l-узла.

Утверждение 2. Пусть t,t₁,ј,t_m - термы, x₁,ј,x_m - переменные и t є t[x₁,ј,x_m], m і 1. Тогда алгоритм Sub переводит t-дерево в tў-дерево так, что tў є t[t₁,ј,t_m].

Ереванский научно-исследовательский институт
автоматизированных систем управления

Литература

1. Barendregt H.P. The lambda calculus, its syntax and semantics. Amsterdam. North Holland. 1981 (рус. пер. Барендрегт Х. Ламбда-исчисление, его синтаксис и семантика. М. Мир. 1985. 606 с.).
2. Нигиян С.А., Аветисян С.А. - Программирование. 2002. N3. С. 5-14 (англ. пер. Nigiyan S.A., Avetisyan S.A. - Programming and Computer Software. 2002. V. 28. N3. P. 119-126).