МАТЕМАТИКА
УДК 517.9
А.Р. Хачатрян
О непрерывности некоторых многозначных отображений
(Представлено чл.- кор. НАН РА Г. Г. Геворкяном 13/II 2004)
Непрерывные многозначные отображения
естественным образом возникают при изучении вопросов корректности и стабильности
в параметризованных задачах оптимизации [1-4]. Известно[1,5], что такие
отображения с выпуклыми замкнутыми значениями имеют непрерывные однозначные
сечения.
В настоящей работе
(при довольно естественных
предположениях) показано, что при e > 0
многозначное отображение ae(q) = { x О a(q)/f(x,q) Ј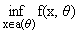 + e} множества e-оптимальных решений
[3 ,4] является непрерывным многозначным отображением с выпуклыми образами и
поэтому имеет непрерывные сечения. Этот результат является основным инструментом
в наших исследованиях.
+ e} множества e-оптимальных решений
[3 ,4] является непрерывным многозначным отображением с выпуклыми образами и
поэтому имеет непрерывные сечения. Этот результат является основным инструментом
в наших исследованиях.
В работе установлены следующие результаты:
а) Методом проекции градиентов строится
функциональная последовательность и при некоторых условиях доказывается, что
расстояние этой последовательности до множества ae(q) равномерно по q стремится к нулю.
б) Вводится понятие интеграла Римана для
многозначного отображения и показывается, что замыкание интеграла Римана
совпадает с интегралом Лебега [6]. Этот результат используется при вычислении
e-субдифференциала целевой функции в стохастическом
программировании.
в) В теории непрерывых игр показано, что если
множества стратегий игроков являются непрерывными многозначными отображения с
выпуклыми образами, то игроки могут использовать только непрерывные решающие
правила, которые описывают устойчивое поведение игроков [7].
г) Рассматривается задача Коши для
дифференциального включения, зависящего от параметров. При некоторых условиях
доказано, что множество решений этой задачи непрерывно зависит от параметров.
д) Показано, что оператор проецирования на
выпуклый компакт в банаховом пространстве есть непрерывное многозначное
отображение.
1. Введение. Пусть X,Y - метрические пространства. Под многозначным отображением (м.о.) X в Y
понимается отображение a : X ® 2Y пространства
X в совокупность всех подмножеств 2Y пространства Y. Напомним
некоторые определения из [8].
Определение 1. М.о. a : X ® 2Y
называется полунепрерывным сверху
(п.н.св.) в точке x0 О X, если из того, что
xj ® x0, yj О a(xj) и yj ®
y0, следует, что y0 О
a(x0).
Определение 2. М.о. a : X ® 2Y
называется полунепрерывным снизу
(п.н.сн.) в точке x0 О X, если для любого
y0 О a(x0) и любой
последовательности {xj}, xj ®
x0, найдутся такие yj О
a(xj), что yj ® y0.
Определение 3. Отображение a : X ® 2Y
называется
непрерывным, если оно одновременно полунепрерывно и сверху и снизу в любой точке
x О X.
Определение 4. Сечение
для a : X ® 2Y определяется как однозначное
отображение y(·) : X ® Y такое, что y(x) О a(x) для всех x О X.
Теорема 1. Пусть a(q) непрерывное м.о. с выпуклыми компактными значениями на
компактном множестве E М Rp. Пусть функция
f(x, q) непрерывна по q
и
выпукла по x О Rn. Положим
Va(q) =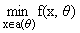 ; ae(q) =
{x О a(q) / f(x,q)
Ј Va(q)
+ e}. Тогда м.о. ae(q) непрерывно.
; ae(q) =
{x О a(q) / f(x,q)
Ј Va(q)
+ e}. Тогда м.о. ae(q) непрерывно.
2. Интегралы многозначного
отображения. Пусть (E,S, P) - вероятностное
пространство, где E М Rp - компакт.
Определение 5. Интегралом Римана м.о. G : E
®
2Rm называется множество интегралов от всевозможных
непрерывных сечений отображения G:
| (R) |
у
х
E
|
G(q)P(dq) ={ |
у
х
E
|
g(q)P(dq)/g(q) О G(q)} є
IR. | |
Определение 6[6]. Интегралом Лебега м.о. G
: E ®
2Rm называется множество интегралов от всевозможных
интегрируемых сечений отображения G. Обозначим это множество через
IL.
Теорема 2. Пусть м.о. G(x,q)
: Rn ×
E ®
2Rm непрерывно; множества G(x,q)
- непустые выпуклые компакты. Пусть a(x) є (R)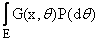 . Тогда м.о. a(x) непрерывно.
. Тогда м.о. a(x) непрерывно.
Теорема 3. Пусть м.о. G
: E ® 2Rm
непрерывно и для любого
q О E множество G(q) выпукло, замкнуто и компактно. Тогда имеет место равенство
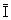 R
= IL, где
R
= IL, где
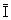 R -
замыкание множества IR.
R -
замыкание множества IR.
Пусть функция f(x,q)
определена на Rn ×
E. При e > 0 определим
e - субдифференциальное отображение по x для функции
f(x,q) следующим образом:
| ¶xef(x,q) є { n О Rn/f(y,q) -
f(x,q) і < n, y -
x > -e,"x О
Rn}. | |
Рассмотрим
теперь задачу стохастического программирования:
| F(x) є |
у
х
E
|
f(x,q)P(dq) ® |
min
|
, | |
где f(x,q) сильно выпукла по x равномерно относительно q О E и непрерывна по q при фиксированом x О
Rn. Имеет место следующий результат:
Теорема 4. Пусть
x0 О Rn. Тогда для любого e > 0 существует d > 0 такое,
что ¶F(x0) +
Bd(0) Н IL Н ¶e F(x0), где IL интеграл Лебега
от многозначного отображения ¶exf(x0,·) :
E ® 2Rn; Be(0) - замкнутый шар радиуса e
с центром в точке нуль.
3. e -
оптимальные решения в параметрических задачах оптимизации. Пусть
f(x,q) удовлетворяет всем условиям теоремы 1 и
существует производная fўx(x,q), непрерывная относительно x и q.
Рассмотрим теперь м.о. aeM(q) = {x О M/f(x,q) Ј V(q) +
e}, где V(q) =
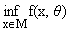 .
.
Теорема 5. Пусть M М Rn - выпуклый компакт и функцинаольная
последовательность {xj(q)} строится
следующими рекуррентными соотношениями:
| x1(q)
є x0 О
M; xj+1(q) =
PM |
ж
и |
xj(q) -
ljfўx(xj(q),q) |
ц
ш |
(j =
1,2,ј). | |
где
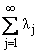 =
+Ґ, lj > 0, ljЇ 0 и PM(x) - проекция точки x на множество M.
=
+Ґ, lj > 0, ljЇ 0 и PM(x) - проекция точки x на множество M.
Тогда для
любого e > 0, r(xj(q),aMe(q)) ® 0 при j ® Ґ равномерно по q О E.
4. Задача о проекции. Пусть M - выпуклый компакт из банахова пространства X и q О X. Рассмотрим задачу
проецирования:
| j(x) є ||q - x|| ® |
min
|
, x О M. | |
Пусть
V(q) =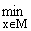 ||q - x||. Положим a(q) є {x О M / ||q - x|| Ј V(q)}.
||q - x||. Положим a(q) є {x О M / ||q - x|| Ј V(q)}.
Теорема 6. М.о. a(q) непрерывно.
5. Приложение к теории игр
и к теории дифференциальных включений.
Теорема 7. Пусть M
- выпуклый компакт из Rn и a(x) : M ®
2Rm - непрерывное м.о. с выпуклыми компактными значениями; f(x,y) -
непрерывная функция, вогнутая относительно y при фиксированном x О M. Тогда имеет место равенство n =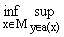 f(x,y) =
f(x,y) =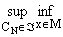 f(x,CN(x)),
где Б -
множество всех
непрерывных сечений м.о. a.
f(x,CN(x)),
где Б -
множество всех
непрерывных сечений м.о. a.
Рассмотрим дифференциальное включение
с начальным условием
Решением этой задачи называется всякая
функция x(t,q) : [a,b] × E ®
Rm, которая непрерывно дифференцируема по t на некотором отрезке
[a,b]; для всех t О [a,b] выполнено соотношение (1) и
x(a,q) = x0. Множество всех решений задачи
(1)-(2) обозначим через Б(q).
Теорема 8. Пусть
выполнены следующие условия:
1) м.о. a(·,q) : Rn ®
2Rm удовлетворяет условию Липшица с константой L > 0
в области W Н Rn
равномерно относительно q О E,
где E - некоторый компакт из Rp, т.е. a(x1,q) Н a(x2,q) + L||x1 - x2||B1(0),
"x1,x2 О
W, "q
О E;
2) при фиксированом x О W м.о. a(x,·) : E ® 2Rm непрерывно;
3) множества a(x,q)
- выпуклые компакты.
Тогда м.о. Б(q) п.н.сн. на E.
Ереванский государственный университет
Литература
1. Tyrrel Rockafellar R., Roger
J-B. Wets Variational Analysis. Springer - Verlag. Berlin
Heidelberg. 1998. 733 p.
2. Хачатрян Р. А. - Изв . НАН Армении. Математика.
2002. 37. N2. С. 65 -76.
3. Хачатрян А. Р., Хачатрян Р. А. - Ученые записки ЕГУ.
2003. N2. С. 3-13.
4. Хачатрян Р.
А., Аветисян Р.A., Хачатрян A. Р. - Изв. НАН Армении. 2003.
N1. С. 69-82.
5. Michael E.
- Ann. Math. 1956. V.63. N2. P.
361-382.
6. Михалевич В. С.,
Гупал А. М., Норкин В. И. Методы невыпуклой оптимизации. М.
Наука. 1987. 279 с.
7. Обен Ж.
П., Экланд И. Прикладной нелинейный анализ. М. Мир. 1988.
510 с.
8. Демьянов В. Ф.,
Васильев Л. В. Недифференцируемая оптимизация. М. Наука.
1981. 384 с.
![]() ; ae(q) =
{x О a(q) / f(x,q)
Ј Va(q)
+ e}. Тогда м.о. ae(q) непрерывно.
; ae(q) =
{x О a(q) / f(x,q)
Ј Va(q)
+ e}. Тогда м.о. ae(q) непрерывно.![]() . Тогда м.о. a(x) непрерывно.
. Тогда м.о. a(x) непрерывно.![]() R
= IL, где
R
= IL, где
![]() R -
замыкание множества IR.
R -
замыкание множества IR.![]() .
.![]() =
+Ґ, lj > 0, ljЇ 0 и PM(x) - проекция точки x на множество M.
=
+Ґ, lj > 0, ljЇ 0 и PM(x) - проекция точки x на множество M.
![]() ||q - x||. Положим a(q) є {x О M / ||q - x|| Ј V(q)}.
||q - x||. Положим a(q) є {x О M / ||q - x|| Ј V(q)}.
![]() f(x,y) =
f(x,y) =![]() f(x,CN(x)),
где Б -
множество всех
непрерывных сечений м.о. a.
f(x,CN(x)),
где Б -
множество всех
непрерывных сечений м.о. a.