|
где
N і 1 - целое. Рассмотрим параметрическую интерполяцию [2,3]
для f О C[-1,1]
Здесь 0 Ј d Ј 2,
если N четное и -1 Ј d Ј 1, если N-нечетное. Наша цель -
получение точных асимптотических L2-констант для интерполяции
Iq,N(f,d).
Определение 1. Скажем,
что q = q(x) О Tq(m),
если выполнены следующие условия:
Для
завершения доказательства достаточно воспользоваться леммой 3. Доказательство
завершается применением леммы 4 с l(t) = g(t)/|t|2p. Этот случай детально
рассмотрен в [4], где показано, что надлежащим выбором параметра s можно
получить более эффективную интерполяцию по сравнению с классической, при
которой, как известно, Например, в случае
q = 7 и s = 11.397712, d = 1 интерполяция
Iq,N(f,d) при нечетных N дает в 85 раз более
точную интерполяцию. В
случае же s < q + 1.5 невозможно применить и теорему 2, из-за условия
(iv) определения 2, но выполнены условия теоремы 3 с p = s и В общем же случае нетрудно убедиться, что
классы Tq(m), q О
Uq(B,m),q О
Vq,p (C) не пересекаются из-за условий
(iv). Институт математики НАН РА
1. Нерсесян А.Б. - ДНАН Армении. 1998. Т. 98. N 1. С.
23-30.
w(e, f) = sup|f(x1) - f(x2)|, x1,x2 О [a,b], |x1 - x2| Ј e.
где кусочно-непрерывная функция
q такая, что еs О Z|q(x + s)| < Ґ, d(x) = еs О Zq(x + s) № 0 и
IN(f, d) =
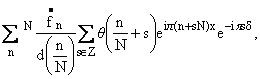
(1)
![]()
=
1
N
е
k N f(xk)e-ipn
xk, xk =
2 k + d
N.
и назовем полиномиально-периодической интерполяцию
Ak(f) = f(k)(1) - f(k)(-1), k = 0,ј, q
(2)
где полиномы Бернулли Bk
определяются рекуррентными соотношениями
Iq,N(f,d) = IN
ж
и f(x) -
q
е
k=0 Ak(f) Bk(x),d
ц
ш +
q
е
k=0 Ak(f)
Bk(x), (3)
B0(x) = x/2, Bk(x) =
у
х Bk-1(x)dx,
у
х 1
-1 Bk(x)dx = 0, x О [-1,1].
2. Асимптотические
L2 -константы. Пусть {fn}, n = 0,±1,±2,ј -
коэффициенты Фурье функции f
Через || · ||
обозначим норму в пространстве L2(-1,1), и
пусть
fn=
1
2
у
х 1
-1 f(x)e-i pn
xdx.

Доказательство следующих двух лемм можно
найти в [2]. Отметим только, что оно основано на очевидном асимптотическом
разложении
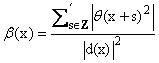 , g(x) = |a(x)|2 + b(x).
, g(x) = |a(x)|2 + b(x).
Лемма 1. Пусть f О Cq+1[-1,1], f(q+2) О L2(-1,1),
As(f) = 0, s = 0,ј,q + 1, q і 0. Тогда
fn=
(-1)n+1
2
q
е
k=0
Ak(f)
(ipn)k+1+
en
2(ipn )q+2, en=
у
х 1
-1 f(q+2)(x)e-ipn
xdx, n № 0.
(4)
е
r О Z ўfn+rNeiprd = o(N-q-2), N ®
Ґ, -[N/2] Ј n Ј -[N/2] + N - 1. (5)
(i) q - кусочно
непрерывная функция на R, для определенности нормированная условием q(x) = 1/2 (q(x + 0) + q(x - 0));
(ii) ряд еs О
Zq(x + s) абсолютно сходится на [-1/2,1/2];
(iii) g(x) ограничена на [-1/2,1/2];
(iv) существует монотонная на (-1/2,0),
а также на (0,1/2), интегрируемая неотрицательная функция m такая, что
Лемма 2. Пусть q О
Tq(m) и верны
условия леммы 1. Тогда
|a(x)|2x-2q-4 Ј m(x), b(x)x-2q-4 Ј m(x).
На основе этих лемм в [2] доказана следующая
теорема.
||f - IN(f,d)|| = o(N-q-1.5), N ® Ґ.
Теорема 1. Пусть q О
Tq(m), f О Cq+1[-1,1], f(q+2) О L2(-1,1), q і 0, тогда
если N ® Ґ, оставаясь четной (s = 0) или нечетной (s = 1).
N2q+3||f - Iq,N(f,d)||2
®
|Aq+1(f)|2
2p2q+4
у
х 1/2
-1/2
е
r
О Z
к
к
к
(-1)rseiprd
(x + r)q+2-
q(x + r)
d(x)
е
s
О Z
(-1)sseipsd
(x + s)q+2к
к
к
2
dx, (6)
Изучим теперь интерполяцию
Iq,N(f, d) для двух других классов q(x).
Определение 2. Мы
скажем, что q О
Uq(B,m), если выполнены
условия (i)-(iii) определения 1 и
(iv) существует константа 0 < B < Ґ
и
монотонная на (-1/2,0), а также на (0,1/2)
и интегрируемая на (-1/2,1/2) неотрицательная функция
m такая, что
и
к
к
к g(x)x-2q-3 - B
xк
к
к Ј m(x),
Определение 3. Мы
скажем, что q О
Vq,p (C), если выполнены условия
(i)-(iii) определения 1 и, кроме того, для некоторого p < q+1.5
существует конечный предел
lim
e® +0
1
ln e
![]()
Лемма 3. Пусть q О
Uq(B,m), q і 0. Тогда (tn = n/N)
(iv)
lim
x®
0 g(x)x-2p = C, 0 < C < Ґ.
Доказательство. Положим h(x) = g(x) x-2q-3. Имеем
lim
N®Ґ
1
2lnN
е
n № 0 N
g(tn)tn-2q-3
n= B.
Теорема 2.
Пусть q О Uq(B,m),
q і 0, f О
Cq+1[-1,1], f(q+2)
О L2(-1,1). Тогда
lim
N®Ґ
ж
з
и
1
2lnN
е
n
№ 0 N
h(tn)
n- B
ц
ч
ш
=
lim
N®Ґ
ж
з
и
1
2lnN
N
е
n=1
h(tn) - h(-tn) - 2B
nц
ч
ш
Ј
const
lim
N®Ґ
ж
з
и
w
ж
з
и
[
![]() ]
]
N,h
ц
ч
ш
+
1
2NlnN
е
[![]() ] <
n
] <
n m(tn)
ц
ч
ш
Ј
const
lim
N®Ґ
ж
з
и
w
ж
з
и
[
![]() ]
]
N,h
ц
ч
ш
+
1
lnN
у
х
[![]() ]/N <
x < 1/2
]/N <
x < 1/2 m(x)dx
ц
ч
ш
= 0.
Доказательство. Имеем
lim
N®Ґ
N2q+3
lnN||f - Iq,N(f,d)||2 =
|Aq+1(f)|2
p2q+4B. (7)
где
(согласно разложению (4))
||f - Iq,N(f,d)|| = ||F - IN(F,d)||,
F = F1 + F2, (8)
F1(x) =
е
n О Z ў
F1,neipn
x, F1,n =
(-1)n+1
2
Aq+1(f)
(ipn)q+2, n №
0,
Воспользовавшись
неравенством треугольника, из леммы 2 получим
F2(x) =
е
n О Z ў
F2,neipn
x, F2,n =
1
2(ipn)q+2
у
х 1
-1 f(q+2)(x)e-ipn
xdx, n №
0.
Легко
проверить следующую формулу:
lim
N®Ґ
N2q+3
lnN||F2 - IN(F2,d)||2 = 0.
Отсюда, с помощью
леммы 1, получим
||f - IN(f,d)||2 = 2
е
n N
е
r
О Z
к
к
к
к
к
к
fn+rNeiprd -
q
ж
з
и
n
N+ r
ц
ч
ш
d(
n
N)
е
s
О Z fn+sNeips d
к
к
к
к
к
к
2
. (9)
lim
N®Ґ
N2q+3
lnN||F1 - IN(F1,d)||2 =
|Aq+1(f)|2
p2q+4
lim
N®Ґ
1
2lnN
е
n Nў
g(tn)
tn2q+3
1
n.
![]() .
Если
ряд
.
Если
ряд
![]() абсолютно сходится, то
абсолютно сходится, то
Доказательство. Имеем
lim
N®Ґ
е
n Nunl
ж
з
и
n
Nц
ч
ш = C
е
n О Z un.
к
к
к C
е
n О Z un -
е
n Nunl
ж
з
и
n
Nц
ч
ш к
к
к Ј
е
|n| Ј [![]() ]
]
к
к
к C - l
ж
з
и
n
Nц
ч
ш к
к
к |un| +
const
е
[![]() ] < |n|
] < |n| |un| Ј
Теорема 3. Пусть f О Cq+1[-1,1],
f(q+2) О L1[-1,1], q і 0 и q О
Vq,p(C). Тогда
w([
![]() ]/N,l)
]/N,l)
е
n О Z |un| +
const
е
|n| > [![]() ]
] |un| = o(1), N ® Ґ.
Доказательство. Имеем
lim
N®Ґ N2p||f - Iq,N(f,d)||2 =
C
2p2q+2
е
n О Z ў
1
|n|2q+2-2 p
к
к
у
х 1
-1 f(q+1)(x)e-ipn xdx
к
к 2
. (10)
где, согласно разложению (4),
||f(x) - Iq,N(f,d)|| = ||F(x) - IN(F,d)||, (11)
Воспользовавшись
теперь формулой (9),
после несложных оценок, получим (tn = n/N)
F(x) =
е
n О Z ў
Fn eipn
x, Fn =
en
2(ipn)q+1, en =
у
х 1
-1 f(q+1)(x)e-ipn
xdx.
lim
N®Ґ N2p||f - Iq,N(f,d)||2 = 2
lim
N®Ґ N2p
е
n
№ 0 N|Fn|2 g(tn) =
1
2p2q+2
lim
N®Ґ
е
n
№ 0 N
g(tn)
|tn|2p
|en|2
|n|2q+2-2p.
и вычислим функции d,a,b и g (x
О [-1/2,1/2])
q(x) =
м
н
о
coss
p
2x,
|x| Ј
1,
0,
|x| >
1,
s > 0. (12)
d(x) = coss
p
2x + sins
p
2|x|,
Таким
образом, если s > q + 1.5 то q О Tq(m),
где m(x) = [const/(|x|2q+4-2s)]. Поэтому можно
применить теорему 1, откуда
a(x) =
sins
p
2|x|
coss
p
2x + sins
p
2|x| , b(x) =
sin2s
p
2|x|
(coss
p
2x + sins
p
2|x|)2 , g(x) = 2a2(x).
где
Nq+1.5||f - Iq,N(f,d)|| ® |Aq+1(f)|
b(q,s,d,s), N ® Ґ,
b(q,s,d,s) =
1
pq+2
й
к
л у
х 1
0
к
к
к
a(x)
xq+2- (1 - a(x))
е
r О Z ў
(-1)rseipr d
(x + r)q+2к
к
к 2
dx +
1
2q + 3щ
ъ
ы 1/2
.
q(x) =
м
п
н
п
о
1,
|x| <
1/2,
1/2,
x = ±1/2,
0,
|x| >
1/2.
const |x|. Тогда, согласно теореме 2,
lim
N®Ґ
Nq+1.5
(lnN)[1/2]||f - Iq,N(f,d)|| =
|Aq+1|
![]()
.
lim
N®Ґ Ns||f - Iq,N(f,d)|| =
1
2spq+1-s
ж
з
и
е
n О Z ў
1
|n|2q+2-2s
к
к у
х 1
-1 f(q+1)(x)e-ipn xdx
к
к 2
ц
ч
ш 1/2
.
для (q + 1) различных
значений {ns}, при
fns=
(-1)ns+1
2
q
е
k=0
Ak(f)
(ipns)k+1, s = 0, 1, ...,
q, const N Ј |ns| Ј N, N ® Ґ.
Работа выполнена в рамках проекта ISTC A-823.
2. Nersessian A.B.
- Numer. Functional Anal. and Optimization. 2000. V. 21. N.
1-2.
3. Нерсесян А.Б., Погосян
А.В. - Изв. НАН Армении. Математика. 2001. Т. 36. N 3. С.
59-77.
4. Nersessian A.B.,
Poghosyan A.V. To be published in Proceedings of ISAAC IV
Conference of Complex Analysis, Differential Equations and Related Topics.
September 17-21. 2002. Yerevan Armenia.
5. Eckhoff K.S. - Math. Comp. 1995. V. 64. N 210.
P. 671 - 690.
6. Eckhoff K.S.,
Wasberg C.E. Thesis of Carl Erik Wasberg, Department of
Mathematics, University of Bergen, Norway, 1996.
7. Крылов А. Лекции по приближенным вычислениям. Л. Изд. АН СССР. 1933.