МЕХАНИКА
УДК 539.3
С. А. Мелкумян, В. С. Тоноян
Контактная задача термоупругости для ортотропной
полуплоскости с вертикальным конечным разрезом
(Представлено академиком Б.Л. Абрамяном 21/V 2003)
Рассматривается плоская контактная задача
термоупругости для ортотропной полуплоскости (z і
0, |x| < Ґ) с вертикальным конечным разрезом (0 < z < b) начиная
с горизонтальной границы (z = 0). Главное направление ортотропии полуплоскости
совпадает с направлением координатной оси.
На конечном участке границы (|x| Ј a)
полуплоскости приложен горячий жесткий штамп с основанием произвольной гладкой
формы, расположенный симметрично относительно оси разреза (x = 0). Предполагается,
что трение между штампом и полуплоскостью отсутствует, а граница вне штампа и
разрез теплоизолированы. Также для простоты принимается, что граница
полуплоскости вне штампа свободна от внешних напряжений, а в разрезе действует
только нормальное давление.
Рассматривается плоское деформированное
состояние (Uy = 0,
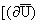 /(¶y)] = 0, [(¶T)/(¶y)] = 0), и задача решается
методом Фурье, когда в качестве основных неизвестных принимаются перемещения
(Ux(x,z),Uz(x,z)) и температурная функция (T(x,z)).
Решение задачи ищется в виде суммы интегралов Фурье. Поиск произвольных функций
интегрирования в конечном счете сводится к решению системы из трех "парных"
интегральных уравнений. Эта система, в свою очередь, сводится к интегральному
уравнению Фредгольма второго рода. Показано, что решение последнего уравнения
может быть найдено методом последовательных приближений. Выведены все расчетные
формулы для определения напряженно-деформированного состояния в любой точке
полуплоскости.
/(¶y)] = 0, [(¶T)/(¶y)] = 0), и задача решается
методом Фурье, когда в качестве основных неизвестных принимаются перемещения
(Ux(x,z),Uz(x,z)) и температурная функция (T(x,z)).
Решение задачи ищется в виде суммы интегралов Фурье. Поиск произвольных функций
интегрирования в конечном счете сводится к решению системы из трех "парных"
интегральных уравнений. Эта система, в свою очередь, сводится к интегральному
уравнению Фредгольма второго рода. Показано, что решение последнего уравнения
может быть найдено методом последовательных приближений. Выведены все расчетные
формулы для определения напряженно-деформированного состояния в любой точке
полуплоскости.
В частных случаях, когда длина разреза
стремится к нулю или к бесконечности, показано, что получается контактная задача
плоской теории термоупругости для полуплоскости без разреза и для
четвертьплоскости (квадранта) соответственно.
Так как задача симметрична относительно оси
разреза (x = 0), то можно ограничиться рассмотрением
только четверти плоскости (0 < x
< Ґ, 0 < z < Ґ), соответствующей граничным условиям:
| qx(0,z) = 0, (0 < z <
Ґ), | |
(1) |
| T(x,0) = f1(x), (0 < x
Ј a), qz(x,0) = 0, (a
< x < Ґ), | |
(2) |
| tzx(x,0) = 0, (0 < x < Ґ), txz(0,z) = 0, (0 < z < Ґ), | |
(3) |
| uz(x,0) = f2(x), (0
< x Ј a), sz(x,0) = 0, (a < x < Ґ), | |
(4) |
| sx(0,z) = f3(z), (0 <
z < b), ux(0,z) = 0, (b Ј z < Ґ). | |
(5) |
Решение задачи ищем в виде сумм интегралов
Фурье:
|
| ux(x,z) = |
Ґ
у
х
0
|
a |
U
|
(a,z)sinaxda + |
Ґ
у
х
0
|
b |
U
|
*
|
(b,x)cosbzdb, | |
| uz(x,z) = |
Ґ
у
х
0
|
a |
W
|
(a,z)cosaxda + |
Ґ
у
х
0
|
b |
W
|
*
|
(b,x)sinbzdb, | |
| T(x,z) = |
Ґ
у
х
0
|
a2 |
T
|
(a,z)cosaxda + |
Ґ
у
х
0
|
b2 |
T
|
*
|
(b,x)cosbzdb, | |
|
| |
| |
(6) |
Затухающие в бесконечности неизвестные
плотности интегралов Фурье (6) представляются в виде:
|
|
U
|
(a,
z) = |
1
c11
|
|
2
е
j=1
|
D1(tj)Aj(a)e-atjz - |
1
c11
|
C(a)e-[(a)/(l)]z, | |
|
U
|
*
|
(b,x) = |
1
c11
|
|
2
е
k=1
|
|
D1(tk)
tk2
|
Bk(b)e -[(b)/(tk)]x - |
l
c11
|
D(b)e-lbx, | |
|
W
|
(a,
z) = |
1
c44
|
|
2
е
j=1
|
D2(tj)Aj(a)e-atjz - |
1
l
|
|
k*
c11
|
C(a)e -[(a)/(l)]z, | |
|
W
|
*
|
(b,x) = |
1
c11
|
|
2
е
k=1
|
D2(tk)Bk(b)e -[(b)/(tk)]x - |
k*
c44
|
D(b)e-lbx, | |
|
T
|
(a,
z) = |
1
l2
|
· |
d
T0g11
|
C(a)e-[(a)/(l)]z, |
T
|
*
|
(b,
x) = - |
d
g11T0
|
D(b)e-lbx. | | |
| |
(7) |
Здесь Aj(a), Bk(b), C(a), D(b) - неизвестные функции
интегрирования, которые можно определить из условий (1)-(5), а плотности и
коэффициенты, входящие в (7) определяются по формулам:
|
| D1(tk) = |
ж
з
и
|
|
c13
c44
|
+ 1 |
ц
ч
ш
|
tk,
D2(tk) = 1 - |
c44
c11
|
tk2, | |
| k* = |
|
l33
l11
|
- |
c44
c11
|
- |
g33
g11
|
|
ж
з
и |
|
l33
l11
|
- |
c44
c11
|
ц
ч
ш |
|
|
c33
c44
|
- |
l33
l11
|
- |
g33
g11
|
· |
c13 + c44
c44
| |
, | |
| d = |
|
l33
l11
|
|
ж
з
и |
1 + |
c13 + c44
c44
|
· |
c13 + c44
c11
|
ц
ч
ш |
- |
c44
c11
|
| T0 |
ж
з
и |
|
c33
c44
|
- |
l33
l11
|
- |
g33
g11
|
· |
c13 + c44
c44
|
ц
ч
ш
| |
. | | |
| |
(8) |
Из решения биквадратного уравнения
|
c33
c11
|
t4 + |
ж
з
и |
|
c13c13
c44c11
|
+ 2 |
c13
c11
|
- |
c33
c44
|
ц
ч
ш |
t2 + 1 = 0 | |
(9) |
определяется tk (
Re tk > 0).
В формулах (6)-(9) имеем:
c11, c13, c33 и c44 -
модули упругости материала, l2 = [(l33)/(l11)] -
отношение коэффициентов теплопроводности тела в направлении оси 0z и
перпендикулярном к ней, g11, g33 - температурные коэффициенты механических
напряжений, соответственно по направлению оси 0x и 0z, T =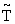 - T0 - относительная, абсолютная и начальная
температура. - T0 - относительная, абсолютная и начальная
температура.
Используя основные соотношения теории
термоупругости [1,2] для исследуемой среды и (6), (7), можно все компоненты
термоупругого поля выразить через Aj(a),
Bk(b), C(a) и
D(b):
| sx(x,z) = |
Ґ
у
х
0
|
a2 |
s
|
x
|
(a,z)cosaxda + |
Ґ
у
х
0
|
b2 |
s
|
*
z
|
(b,x)cosbzdb, | |
| sz(x,z) = |
Ґ
у
х
0
|
a2 |
s
|
z
|
(a,z)cosaxda + |
Ґ
у
х
0
|
b2 |
s
|
*
x
|
(b,x)cosbzdb, | |
|
| tzx(x,z) = |
Ґ
у
х
0
|
a2 |
t
|
zx
|
(a,z)sinaxda + |
Ґ
у
х
0
|
b2 |
t
|
*
zx
|
(b,x)sinbzdb, | |
| qx(x,z) = |
Ґ
у
х
0
|
a3 |
q
|
x
|
(a,z)sinaxda + |
Ґ
у
х
0
|
b3 |
q
|
*
x
|
(b,x)cosbzdb, | |
| qz(x,z) = |
Ґ
у
х
0
|
a3 |
q
|
z
|
(a,z)cosaxda + |
Ґ
у
х
0
|
b3 |
q
|
*
z
|
(b,x)sinbzdb. | | |
| |
(10) |
|
|
Здесь:
|
|
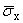 (a,z) = (a,z) = |
2
е
j=1
|
|
й
к
л
|
D1(tj) - |
c13
c44
|
D2(tj)tj |
щ
ъ
ы
|
Aj(a)e-atjz +
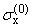 C(a)e-[(a)/(l)]z, C(a)e-[(a)/(l)]z, | |
|
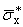 (b,x) = (b,x) = |
2
е
k=1
|
|
й
к
л
|
- |
D1(tk)
tk3
|
+ |
c13
c44
|
D2(tk) |
щ
ъ
ы
|
Bk(b)e-[(b)/(tk)]x -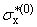 D(b)e-lbx, D(b)e-lbx, | |
|
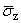 (a,z) = (a,z) = |
2
е
j=1
|
|
й
к
л
|
c13
c11
|
D1(tj) - |
c33
c44
|
D2(tj)tj |
щ
ъ
ы
|
Aj(a)e-atjz +
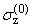 C(a)e-[(a)/(l)]z, C(a)e-[(a)/(l)]z, | |
|
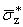 (b,x) = (b,x) = |
2
е
k=1
|
|
й
к
л
|
- |
c13
c11
|
· |
D1(tj)
tk3
|
+ |
c33
c44
|
D2(tj) |
щ
ъ
ы
|
Bk(b)e-[(b)/(tk)]x -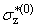 C(b)e-lbx, C(b)e-lbx, | |
|
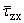 (a,z) = (a,z) = |
2
е
j=1
|
|
й
к
л
|
c44
c11
|
D1(tj)tj +
D2(tj) |
щ
ъ
ы
|
Aj(a)e-atjz +
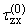 C(a)e-[(a)/(l)]z, C(a)e-[(a)/(l)]z, | | |
| |
|
|
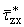 (b,x) = - (b,x) = - |
2
е
k=1
|
|
й
к
л
|
c44
c11
|
· |
D1(tj)
tk2
|
- |
D2(tk)
tk
|
щ
ъ
ы
|
Bk(b)e-[(b)/(tk)]x +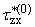 D(b)e-lbx, D(b)e-lbx, | |
|
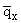 (a,z) = qx(0)C(a)e-[(a)/(l)]z, (a,z) = qx(0)C(a)e-[(a)/(l)]z, |
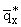 (b,x) = (b,x) =
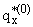 D(a)e-lbx, D(a)e-lbx, | |
|
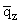 (a,z) = qz(0)C(a)e-[(a)/(l)]z, (a,z) = qz(0)C(a)e-[(a)/(l)]z, |
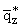 (b,x) = (b,x) =
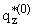 D(a)e-lbx, D(a)e-lbx, | | |
| |
(11) | где
|
| sx(0) = |
c13
c44
|
· |
k*
l2
|
- |
d
T0l2
|
-1, 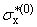 = l2 - = l2 - |
c13
c44
|
k* + |
d
T0
|
, | |
| sz(0) = |
c33
c44
|
· |
k*
l2
|
- |
c13
c11
|
- |
d
T0l2
|
,
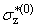 = = |
c13
c11
|
l2 - |
c33
c44
|
k* + |
d
T0
|
· |
g33
g11
|
, | |
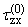 = = |
ж
з
и
|
|
c44
c11
|
+ k* |
ц
ч
ш
|
|
1
l
|
,
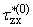 = = |
ж
з
и
|
|
c44
c11
|
+ k* |
ц
ч
ш
|
l, | |
| qx(0) = |
d
g11
|
· |
l11
T0l2
|
,
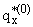 = - = - |
d
g11
|
· |
l11l
T0
|
, | |
| qz(0) = |
d
g11
|
· |
l33
T0l3
|
,
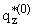 = - = - |
d
T0
|
· |
l33
g11
|
. | | |
| |
(12) | Удовлетворяя граничным условиям (1) и (3), получаем:
| Aj(a) = ajAj(a) + bjC(a), | |
(14) |
где
|
| a1 = 1, b1 = 0, a2 = - |
a11
a12
|
, b2 = |
tzx(0)
a12
|
, b1* = 1, b2* = - |
b11
b12
|
, | |
| a1j = |
c44
c11
|
D1(tj)tj + D2(tj), j = 1,2,
b1k = |
c44
c11
|
· |
D1(tk)
tk2
|
- |
D2(tk)
tk
|
, k = 1,2. | | |
| |
(16) |
Имея в виду (13), (14), (15) и
удовлетворяя смешанным граничным условиям (2), (4), (5), решение задачи сведено
к решению следующих систем из трех парных интегральных уравнений [3]:
|
м
п
п
н
п
п
о |
|
Ґ
у
х
0
|
a2C(a)cosaxda = |
l2T0g11
d
|
f1(x) (0 < x
Ј a), | |
|
Ґ
у
х
0
|
a3C(a)cosaxda =
0 (0 < x < Ґ) | | |
| |
(17) |
|
м
п
п
н
п
п
о |
|
Ґ
у
х
0
|
aA1(a)cosaxda =
f2*(x) (0 < x
Ј a), | |
|
Ґ
у
х
0
|
a2a1(a)cosaxda =
f4(x) - |
1
m21
|
|
2
е
k=1
|
b1k* |
Ґ
у
х
0
|
b2e-[(b)/(
tk)]xB1(b)db (a < x <
Ґ), | | |
| |
(18) |
|
м
п
п
н
п
п
о |
|
Ґ
у
х
0
|
b2B1(b)cosbzdb =
f3*(z) - |
1
n11
|
|
2
е
j=1
|
a2jaj |
Ґ
у
х
0
|
a2e-atjzA1(a)da (0 < z <
b) | |
|
Ґ
у
х
0
|
bB1(b)cosbzdb =
0 (b Ј z <
Ґ), | | |
| |
(19) | где
|
| f2*(x) = |
1
m11
|
f2(x) - |
m12
m11
|
|
Ґ
у
х
0
|
aC(a)cosaxda, | |
| f4(x) = - |
m22
m21
|
|
Ґ
у
х
0
|
a2C(a)cosaxda, | |
| f3*(z) = |
1
n11
|
f3(z) - |
1
n11
|
|
2
е
j=1
|
a2jbj |
Ґ
у
х
0
|
a2e-atjzC(a)da - |
1
n11
|
sx(0) |
Ґ
у
х
0
|
a2e-[(a)/(l)]z C(a)da, | |
| m11 = |
1
c44
|
|
2
е
j=1
|
D2(tj)aj,
m12 = |
1
c44
|
|
й
к
л
|
2
е
j=1
|
D2(tj)bj - |
k*
l
|
щ
ъ
ы
|
, | |
| m21 = |
2
е
j=1
|
|
й
к
л
|
c13
c11
|
D1(tj) - |
c33
c44
|
D2(tj)tj |
щ
ъ
ы
|
aj, m22 = |
2
е
j=1
|
|
й
к
л
|
c13
c11
|
D1(tj) - |
c33
c44
|
D2(tj)tj |
щ
ъ
ы
|
bj + sz(0), | |
| n11 = |
2
е
k=1
|
|
й
к
л
|
- |
D1(tk)
tk3
|
+ |
c13
c44
|
D2(tk) |
щ
ъ
ы
|
bk*,
a2j = D1(tj) - |
c13
c44
|
D2(tj)tj, | | |
| |
(20) |
решения, подобные (17), (18), (19)
- парные интегральные уравнения рассматривались в работах [4-7] и др.
Решая эти уравнения методом преобразующих
операторов, получаем:
| C(a) = - |
2
p
|
· |
1
a2
|
|
a
у
х
0
|
tj1(t)J1(at)dt | |
(21) |
|
| A1(a) = - |
2
p
|
· |
1
a
|
|
a
у
х
0
|
hj2(h)J1(ah)dh - |
2
p
|
· |
1
a
|
|
Ґ
у
х
a
|
j4(h)J1(ah)dh + | |
| + |
2
p
|
· |
1
a
|
· |
1
m21
|
|
2
е
k=1
|
b1k* |
Ґ
у
х
0
|
b2B1(b)db |
Ґ
у
х
a
|
hK1 |
ж
з
и
|
|
b
tk
|
h |
ц
ч
ш
|
J1(ah)dh, | | |
| |
(22) |
| B1(b) = |
2
p
|
· |
1
b
|
|
b
у
х
0
|
rj3(r)J0(br)dr - |
1
n11
|
|
2
е
j=1
|
a2jaj |
b
у
х
0
|
r[ I0(atjr) - L0(atjr)] J0(br)dr, | |
(23) | где
| j1(t) = |
l2T0g11
d
|
· |
d
dt
|
|
t
у
х
0
|
|
f1(x)
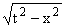 |
dx, j2(h) = |
d
dh
|
|
h
у
х
0
|
|
f2*(x)
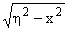 |
dx, | |
| j4(h) = |
Ґ
у
х
h
|
|
xf4(x)
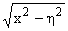 |
dx, j3(r) = |
r
у
х
0
|
|
f3*(z)
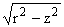 |
dz, | |
Ji(x) -
функция Бесселя первого рода от действительного аргумента, Ki(x) -
функция Макдональда, Ii(x) - функция Бесселя первого рода от мнимого
аргумента, Li(x) - функция Струве от мнимого аргумента.
Исключая A1(a) из (22) и (23), для определения B(b) получаем следующее интегральное уравнение Фредгольма
второго рода:
| B(b) = W(b) + |
Ґ
у
х
0
|
B(g)K(g,b)dg, | |
(24) | где
|
| W(b) = |
2
p
|
|
у
х
|
b
0
|
rj3(r)J0(br)dr + |
2
p
|
· |
1
n11
|
|
2
е
j=1
|
a2jaj |
й
л
|
|
a
у
х
0
|
hj2(h)dh+ | |
| + |
Ґ
у
х
a
|
j4(h)dh |
щ
ы
|
|
Ґ
у
х
0
|
aJ1(ah)da |
b
у
х
0
|
rJ0(br) |
й
л
|
I0(atjr) - L0(atjr) |
щ
ы
|
dr, | | |
| |
(26) |
|
| K(g,b) = |
2
p
|
· |
1
n11
|
· |
g
m21
|
|
2
е
j=1
|
a2jaj |
2
е
k=1
|
b1k* |
Ґ
у
х
a
|
hK1 |
ж
з
и
|
|
g
tk
|
h |
ц
ч
ш
|
dh · | |
| · |
Ґ
у
х
0
|
aJ1(ah)da |
b
у
х
0
|
rJ0(br) |
й
л
|
L0(atjr) - I0(atjr) |
щ
ы
|
dr. | | |
| |
(27) |
Исходя из результатов [4], доказана
разрешимость уравнения (24). Решая (24) методом последовательных приближений,
определяем B(b) = bB1(b), далее по формулам
(22), (15) и (14) определяем все искомые функции.
Используя формулы (12), (11), (10), (8), (7)
и (6), можно определить все компоненты термоупругого поля в любой точке
полуплоскости.
В частности, температурный поток и напряжения
под штампом, а также напряжения вне разреза определяются по формулам:
| qz(x,0) = |
2
p
|
qz(0) |
aj1(a)
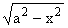 |
- |
2
p
|
qz(0) |
a
у
х
x
|
|
j1(t) - tj1ў(t)
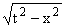 |
dt (0 < x <
a), | |
| sz(x,0) = |
2
p
|
· |
m22aj1(a) + m21[aj1(a) - j4(a) + F(a)]
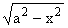 |
- | |
| - |
2
p
|
|
a
у
х
x
|
|
m21[j2(h) + hj2ў(h)] + m22[j1(h) + hj1ў(h)]
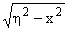 |
dh + | |
| + |
2
p
|
m21 |
Ґ
у
х
a
|
|
j4ў(h) - Fў(h)
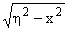 |
dh + |
2
е
k=1
|
bk* |
infty
у
х
0
|
b2e-btk-1xB1(b)db
(0 < x < a), | |
|
| sx(0,z) = - |
2
p
|
n11z |
j3(b) + F1(b)
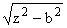 |
+ | |
| + |
2
p
|
n11z |
b
у
х
0
|
|
jў3(r) + Fў1(r)
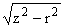 |
dr + |
2
е
j=1
|
a2jaj |
Ґ
у
х
0
|
a2e-atjzA1(a)da + | |
| + |
2
е
j=1
|
a2jbj |
Ґ
у
х
0
|
a2e-atjzC(a)da + sx(0) |
Ґ
у
х
0
|
a2e-[(a)/(l)]zC(a)da (b < z <
Ґ), | | |
| |
(28) | где
|
| F(h) = |
h
m21
|
|
2
е
k=1
|
b1k* |
Ґ
у
х
0
|
b2K1 |
ж
з
и
|
|
b
tk
|
h |
ц
ч
ш
|
B1(b)db, | |
| F1(r) = - |
p
2
|
· |
1
n11
|
|
2
е
j=1
|
a2jaj |
Ґ
у
х
0
|
a2 |
й
л
|
I0(atjr) - L0(atjr) |
щ
ы
|
A1(a)da. | | |
| |
(29) |
Институт механики НАН РА
ЕрГУАС
Литература
1. Новацкий В. Вопросы термоупругости. М. 1962. 364
с.
2. Уздалев А.И. Некоторые задачи термоупругости анизотропного тела. Изд. Сарат. ун-та.
1967. 167 с.
3. Градштейн И.С.,
Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений.
М. Наука. 1971. 1108 с.
4. Тоноян
В.С., Мелкумян С.А. - ДАН Арм. 1991. Т. 92. N 3. С.
133-137.
5. Мелкумян С.А.
- ДАН АрмССР. 1972. N 2. С.
82-93.
6. Тоноян В.С., Мелкумян
С.А. - ДАН АрмССР. 1970. Т. 1. N 3. С.
144-149.
7. Уфлянд Я.С.
Метод парных уравнений в задачах математической физики. Л.
Наука. 1977. 220 с.
|