УДК 539.1
Плоская задача соударения упругих двугранных углов
(Представлено 13/I 2003)
|
|
Рассматривается линейная задача соударения упругих тел, которые в момент соударения ограничены цилиндрическими поверхностями x = f(|z|). Предполагается, что после соударения имеется полный контакт тел и они состоят из одинакового материала, из чего следует, что после соударения они сливаются и движутся как единое целое. Волновая картина, получающаяся после соударения, зависит от формы тел, в частности, имеющих форму одинаковых клиньев. Эта задача имеет практическое применение в сейсмологии. Начальные условия, соответствующие решению задачи соударения неограниченных по оси y двугранных углов раствора 2
|
(1) |
Здесь uz,x - компоненты
перемещения, s(x) - единичная функция.
Введем преобразование по Лапласу по t от
функций ux, uz, а именно
![]() ,
,
![]() ,
тогда уравнения теории упругости в изображениях имеют вид:
,
тогда уравнения теории упругости в изображениях имеют вид:
|
(2) |
где a, b - скорости продольных и
поперечных упругих волн.
Из закона сохранения количества движения в
предположении, что массы тел одинаковы, следует, что после слияния они имеют
скорость [(Vў)/2] и все последующие выкладки имеют
место в системе координат, движущейся по оси x со скоростью [(Vў)/2], в которой тела после соударения неподвижны. Далее
вводится преобразование Фурье по x, z
|
(3) |
где s = -iw есть параметр преобразования
Лапласа. Переходя к оригиналам, проводя контуры по
a в комплексной плоскости через точки Смирнова -
Соболева Определим вначале решение вне точечных волн,
позади плоских продольных волн AB: x = kz -at соответствующее решению позади
плоских волн для z > 0. Точнo так же получается решение позади продольных
волн A1B1: x = kz + at Теперь найдем [(¶ux)/(¶x)],
[(¶uz)/(¶z)]
внутри точечных волн. Из (9) с учетом
[(¶a1,2)/(¶t)] = -[1/(fў1,2(a1,2))]
получим: Вычисляя интегралы, вводя полярные
координаты x = rcosj, z = rsinj,
отделяя действительные части в (11) и записывая ветвь арктангенса, для которой
Из (2), (3) после обращения преобразования
Фурье можно получить:
Вычисляя интегралы, получим:
![]() x
x
=
b2a2 + a2g2 - 1
(a2a2 + b2g2 - 1)(b2a2 + a2g2 - 1) - (a2 - b2)2a2g2×
×
1
s2(2p)2
Ґ
уу
хх
-Ґ es(axў+gzў){
V0s(xў- k(|zў|)) - (V0 + Vў)s(k(|zў|) - xў)} dxўdzў,
![]() z
z
= -
(a2 - b2)ag
b2a2 + a2g2 - 1
![]() x
x
. (4)
Поскольку
Ґ
у
х
-Ґ esgzўdzў
Ґ
у
х
k|zў| esgxўV0dxў-
Ґ
у
х
-Ґ esgzў(V0 + Vў)dzў
k|zў|
у
х
-Ґ esaxўdxў=
=
2V0 + Vў
-s2k
g2 - a2k2. (5)
из
(4), (5) можно получить:
(a2a2 + b2g2 - 1)(b2a2 + a2g2 - 1) - (a2 - b2)2a2g2 = a2b2(g2 - g12)(g2 - g22),
g12 =
1
a2- a2,
g22 =
1
b2- a2,
Подставляя (6) в (3) и вычисляя при
z > 0 вычеты в точках
![]() x
x
=
b2a2 + a2g2 - 1
2D(2V0 + Vў)k,
![]() z
z
= -(2V0 + Vў)k(a2 - b2)
ag
2D,
D = (pabsw)2(g2 - a2k2)(g2 - g12)(g2 - g22). (6) ![]() =
=![]() 1,2, можно получить:
1,2, можно получить:
![]() =
=Ґ
у
х
-Ґ e-s(ax+g1z)i
a2
2s2(g12 - a2k2)g1(2V0 + Vў)kda +
+
Ґ
у
х
-Ґ e-s(ax+gz)2i
g2
2pa2s2(g22 - a2k2)(2V0 + Vў)kda, (7)
![]() = -(2V0 + Vў)k
= -(2V0 + Vў)kм
н
о
-
Ґ
у
х
-Ґ e-s(ax+g1z)i
a
2ps2(g12 - a2k2)da +
+
Ґ
у
х
-Ґ e-s(ax+g2 z)i
a
2ps2(g22 - a2k2)da
ь
э
ю
, (8)
и
вычисляя интегралы от дельта-функций, можно получить
f1,2(a1,2) = t - a1,2x - g1,2(a1,2)z,
f1,2(a1,2) = 0
¶2ux
¶x¶t= -
(2V0 + Vў)k
p
Re
i
м
н
о
a13
g1(g12 - a12k2)fў1(a1)+
g2a2
(g22 - a22k2)fў2(a2)ь
э
ю
,
¶2uz
¶x¶t=
(2V0 + Vў)k
p
Re
i
м
н
о
-
a12
(g12 - a12k2)fў1(a1)+
a22
(g22 - a22k2)fў2(a2)ь
э
ю
. (9) ![]() , и поперечных плоских волн: x = kz - bt
, и поперечных плоских волн: x = kz - bt![]() , для этого
следует вычислить вычеты в (7), (8) в точках a = -[1/(a
, для этого
следует вычислить вычеты в (7), (8) в точках a = -[1/(a![]() )], a = -[1/(b
)], a = -[1/(b![]() )]. Отсюда получим решение вне точeчных
волн для x < 0:
)]. Отсюда получим решение вне точeчных
волн для x < 0:
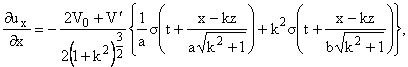
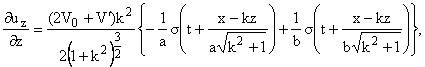
(10) ![]() , и поперечных волн: x = kz + bt
, и поперечных волн: x = kz + bt![]() . При этом, вычислив вычеты в (7),(8) в
точках a = [1/(a
. При этом, вычислив вычеты в (7),(8) в
точках a = [1/(a![]() )], a =
[1/(b
)], a =
[1/(b![]() )], получим решение (10)
позади идущих вправо плоских волн для x > 0 с соответствующей заменой
единичных функций. Таким образом, между плоскими волнами AB и
A1B1
)], получим решение (10)
позади идущих вправо плоских волн для x > 0 с соответствующей заменой
единичных функций. Таким образом, между плоскими волнами AB и
A1B1
а
между соответствующими поперечными плоскими волнами добавится
¶ux
¶x=-
2V0 + Vў
2(1 + k2)[3/2]a,
¶uz
¶z= -
(2V0 + Vў)k2
2(1 + k2)[3/2]a,
-
2V0 + Vў
2(1 + k2)[3/2]ak2,
(2V0 + Vў)k2
2(1 + k2)[3/2]a.
причем
¶ux
¶x=
(2V0 + Vў)k
p
Re
i
м
н
о
у
х
a13da1
g1(g12 - a12k2)-
у
х
g2a2da2
g22 - a22k2ь
э
ю
,
¶uz
¶z=
-(2V0 + Vў)k
p
Re
i
м
н
о
-
у
х
a1g1da1
g12 - a12k2+
у
х
g2a2da2
g22 - a22k2ь
э
ю
, (11)
a1 =
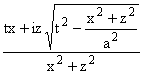 , a2 =
, a2 =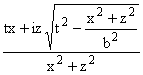 .
.
(12)
|
(13) |
|
(14) |
где cosj0 = [k/(![]() )].
)].
Очевидно, что вне поперечных волн следует
полагать c2 = 0, c4 = 0. Постоянные интегрирования в (13) выбраны
так, чтобы на волнах r = at, r = bt при sinj < cosj0 получить нулевое решение, а при sinj > cosj0, поскольку
выбрана ветвь
Институт механики НАН
Армении
Горисский филиал Государственного
инженерного университета Армении
1. Мартиросян А.Н. Решение некоторых нестационарных граничных задач теории упругости. Канд.
дис. Ереван. 1977. 150 с.