ИНФОРМАТИКА
УДК 510
В.К.Леонтьев, Г.Л.Мовсисян
Об аддитивном канале связи
(Представлено академиком Ю.Г. Шукуряном 12/XII 2003)
Рассматривается аддитивный канал связи в
следующей стандартной формулировке. В множестве Bn - двоичных наборов
длины n выделено произвольное подмножество S, содержащее нулевой вектор, и любое
кодовое слово v на выходе воспринимается как
где e О S, а v О
Bn. Таким образом S - это множество векторов ошибок в стандартных
терминах теории корректирующих кодов. Многие классические каналы можно
представить в форме (1), что и определяет интерес к этому достаточно
универсальному каналу [1-3]. Классической задачей теории корректирующих кодов
является построение кода максимальной мощности, исправляющего ошибки из
множества S. Существуют два универсальных способа для оценки мощности такого
кода: верхняя граница получается методом "плотной упаковки", а нижняя граница
методом "насыщения" или процедурой Варшамова - Гилберта. Одна из известных
проблем теории кодирования в содержательной формулировке звучит следующим
образом: какая из двух упомянутых выше границ ближе к истинному значению
максимальной мощности соответствующего кода [3]? Мы обсуждаем эту проблему в
терминах "структуры" множества ошибок S, а также рассматриваем несколько
отдельных примеров.
Определение [1]. Код V
Н Bn называется кодом, исправляющим ошибки
канала S, если выполняется следующее условие:
для любых кодовых точек u и v и для
любых векторов ошибок e1 и e2 из S.
Условие (2) действительно позволяет исправить
все ошибки канала S с помощью обычной таблицы декодирования. Приведем нижнюю и
верхнюю границы для мощности |V(S)| максимального кода, исправляющего все ошибки из S в
терминах мощности окрестностей 1-го и 2-го порядка, индуцированных этим
множеством.
Определение. Окрестностью 1-го порядка точки v О
Bn, индуцированной множеством S, называется множество
| A1(v) = {v + e, e О S }.
(3) | |
Окрестности следующих порядков определяются
индуктивно, исходя из формулы (3)
| A2(v) =
A1(A1(v)) = {v1 +e, v1
О A1(v),e О S }.
(4) | |
Ясно, что (4)
эквивалентно следующей формуле:
| A2(v) = {v + (ei + ej),ei,ej О
S }. | |
Таким образом, если
S2={(ei+ej),ei,ej О S} -
"квадрат" множества S, то окрестность 2-го порядка A2(v)
определяется формулой
| A2(v) = {v + e,e О S2}.
(5) | |
Аналогично
определяются окрестности любого порядка, индуцированные множеством S.
Примеры.
1. Если S - это шар радиуса t в метрике
Хэмминга с центром в нуле, т.е. S = { x,||x || Ј t }, то S2 - это шар
радиуса 2t с этим же центром при 2t < n.
2. Если S - подгруппа Bn, то
S2 = S.
Нетрудно понять, что все окрестности одного и
того же порядка равномощны, т.е.
| |Ak(v)| =
|Sk| = |Ak| k = 1,2,...
| |
(6) |
Теорема 1. Для мощности
|V(S)| максимального кода,
исправляющего все ошибки из множества S, справедливы неравенства
|
2n
|A2|
|
Ј |V(S)| Ј |
2n
|A1|
|
. | |
(7) |
Доказательство. Верхняя
граница следует прямо из определения (2), которое утверждает, что окрестности
1-го порядка точек из кода V(S) не пересекаются.
Для доказательства нижней границы нужно лишь
модифицировать процедуру Варшамова - Гилберта:
1. пусть v - произвольная точка из
Bn. Положим v1 = v и рассмотрим окрестность 2-го порядка
точки v1, т.е. A2(v1);
2. в качестве v2 выбираем
произвольную точку из { Bn\A2(v1)};
3. в качестве v3 выбираем
произвольную точку из { Bn\( A2(v1)ИA2(v2))};
4. продолжаем эту процедуру до исчерпания
всего Bn.
Относительно построенного кода V(S) =
{v1v2...vN} справедливы следующие
утверждения.
I. Код V(S) исправляет
все ошибки из S.
Действительно, если не так, то
или
т.е.
vi О
A2(vj), что противоречит построению.
II. Мощность |V(S)| кода V(S) удовлетворяет
неравенству
Эта
граница сразу следует из очевидных неравенств
| |A2(v1) И A2(v2) И ј И A2(vN)| Ј |
N
е
i=1
|
|A2(vi)| Ј N|A2| | |
Следствие 1. Если S -
группа, то
Неравенства (7) показывают, что точность
границ Хэмминга и Варшамова - Гилберта определяется отношением |A2|/|A1|, которое
удовлетворяет очевидным неравенствам
В частности, если S =
U1 И U2, где U1,
U2 - подгруппы Bn и |U2| Ј c, то при больших n
| |S2| |
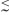 |
c|S| | |
и
границы в (7) отличаются в константу раз.
Таким образом алгебраическая структура
множества S сильно влияет на точность границ в (7).
Примеры.
1. Пусть в канале происходит любое, но четное
число ошибок. Тогда |S| =
2n-1 и |V(S)| = 2. Действительно, точки a = (11...1) и b = (0...0) образуют
код, который исправляет все ошибки из S. Если же в коде V(S) имеется не менее
трех точек, то хотя бы две из них имеют вес одинаковой "четности" и не
могут быть правильно идентифицированы на приемном конце.
2. Рассмотрим канал с "разделением ошибок",
т.е. после искажения канал некоторое время передает символы безошибочно.
Определение. Канал S
называется каналом с разделением ошибок уровня k, если любое слово
x = (x1x2...xn) О S
удовлетворяет следующим неравенствам:
|
м
п
п
н
п
п
о |
|
|
|
|
|
|
|
|
| xn-k+1+xn-k+2+...+xn Ј 1,
| | |
| |
Следующее
утверждение нужно для оценки мощности |S|.
Теорема 2. Если S(n,k) -
число ненулевых решений системы (11), то
| S(n,k) = |
Ґ
е
m=1
|
|
ж
з
и |
|
|
ц
ч
ш |
+ 1.
(12) | |
Доказательство. Пусть
x = (x1x2...xn) - произвольное решение системы
(11) и y1 < y2 < ... < ym - номера
всех единичных координат вектора x. Тогда
| ys - ys-1 і k,
s = 2,3,...m | |
и если
y1=y, то
|
|
|
|
|
| ym = (m - 1)k + y + (z1 + z2 ... + zm-1), | | |
| |
где
zi і 0 и
| z1 + z2 ... + zm-1 Ј n - (m - 1)k + y, | |
Если
em(t) - число решений уравнения
z1 + z2 + ... + zm-1 = t, то em(t) =
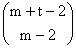 и для
числа Sm(n,k)-решений уравнения (11) с ||x|| = m получаем формулу
и для
числа Sm(n,k)-решений уравнения (11) с ||x|| = m получаем формулу
| Sm(n,k) = |
N
е
t=0
|
em(t) = |
ж
з
и |
|
|
ц
ч
ш |
, | |
где
N = n - (m - 1)k - y.
Для получения финального результата осталось
"освободить" y и просуммировать Sm(n,k) по всем m.
В терминах производящих функций искомый
результат выглядит так.
Пусть
Следствие.
| Fk(z) = |
z
1-z
|
(zk + z - 1)
. | |
(13) |
Для исправления ошибок в канале S можно
использовать код Хэмминга для коррекции одной ошибки в каждом подслове длины k.
Таким образом, мы получили код мощности (для больших n и k) порядка
| |V(S)| |
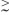 |
2n(1-[lnk/k]). | |
(14) |
Использование (7) и (13) приводит к
следующей верхней границе:
| |V(S)| |
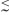 |
2n(1-[(l)/k]), | |
(15) |
где l =
log2 e.
Вычислительный центр РАН
Литература
1. Деза М.Е. - Проблемы передачи информации. 1965. Т. 1. N3. С. 29-39.
2. Гоппа В.Д. - Успехи мат. наук. 1984. N1(35). С. 77-120.
3. Кричевский Р.Е. Сжатие и поиск информации. М. Радио и связь. 167 с.