МАТЕМАТИКА
УДК 518.9
С. Л. Амбарян, В.С. Амбарян
Об одном множестве точек l-встречи при преследовании
с задержкой
(Представлено академиком Ю.Г. Шукуряном 22/VII 2003)
Пусть преследователь P и преследуемый E
осуществляют простое преследование (т.е. перемещаются в плоскости с постоянными
по модулю скоростями a и b
(a > b) соответственно и
имеют возможность в каждый момент времени изменять направление своего движения).
В начальный момент времени t = 0 игрок P находится в начале координат P(0)={0, 0},
а игрок E - в точке с координатами E(0)={a, 0}.
Допустим, что игрок E движется прямолинейно
начиная с момента времени t = 0. Преследуемый E считается пойманным, если
расстояние между ним и преследователем P станет меньше или равно l, т. е. l
і 0, |P(t)E(t)| Ј l. Игрок P применяет следующую
стратегию: он движется прямолинейно по лучу с максимальной скоростью, что
гарантирует ему l-встречу за минимальное время. Обозначим эту стратегию через
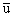 .
.
Геометрическое место точек встречи состоит из
точек M = M(x,y), удовлетворяющих условию
|
|P(0)M|-l
a
|
= |
|E(0)M|
b
|
. | |
(1) |
Уравнение (1) является уравнением
плоской алгебраической кривой, называемой овалом Декарта [1].
Теперь рассмотрим следующую задачу. Игрок P
до момента времени T не получает никакой информации об игроке E и стоит на
месте. С момента времени T игрок P получает информацию о местоположении игрока E
и начинает преследование. Игрок P применяет стратегию
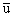 , a игрок E движется прямолинейно. Тогда геометрическое
место точек встречи описывается следующим уравнением:
, a игрок E движется прямолинейно. Тогда геометрическое
место точек встречи описывается следующим уравнением:
|
|P(T)M| - l
a
|
+ T= |
|E(0)M|
b
|
, | |
(2) |
которое также является овалом
Декарта.
Так как игрок P в течение времени T стоит на
месте, то за это время игрок E может оказаться в любой точке окружности
AR(E(0)) с центром E(0) и радиусом R=bT. Для
каждой точки Ej окружности
AR(E(0)) геометрическое место точек встречи описывается следующим
уравнением:
|
|P(T)M| - l
a
|
= |
|EjM|
b
|
, | |
(3) |
где точка Ej=Ej(xEj,yEj) имеет координаты:
| yEj = Rsinj,
где 0 Ј
j Ј 2p и R = bT. | |
Уравнение
(3) определяет семейство овалов Декарта с
параметром j, 0 Ј
j Ј 2p.
Декартов овал (2), т.е. [(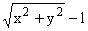 )/(a)] + T = [(
)/(a)] + T = [(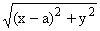 )/(b)], обозначим через DT(l), а множество всех точек
внутренней части овала, включая его границу, через ST(l). Семейство
декартовых овалов (3), т.е.
)/(b)], обозначим через DT(l), а множество всех точек
внутренней части овала, включая его границу, через ST(l). Семейство
декартовых овалов (3), т.е.
обозначим
через DT(l,j).
Имеет место следующая
Теорема. Декартов овал
DT(l) является огибающей для семейства декартовых овалов
DT(l,j), 0 Ј j Ј 2p.
Доказательство. Преобразуем уравнение (3) следующим образом:
| a |
Ц
|
(x - a - Rcosj)2 + (y - Rsinj)2
|
= b( |
|
_____
Цx2+y2
|
- l), | |
|
| F(x,y,j) = a2((x - a - Rcosj)2 + (y - Rsinj)2) - b2( |
_____
Цx2+y2
|
- l)2 = 0, | |
| F(x,y,j) = a2((x - a)2 - 2R(x - a)cosj + R2cos2j) + | |
|
+ (y2 - 2Rysinj + R2sin2j)) - b2( |
_____
Цx2+y2
|
- l)2 = 0, | | |
| |
|
| F(x,y,j) = a2((x - a)2 - 2R((x - a)cosj + ysinj)) + y2 + | |
|
+ R2(sin2j + cos2j)) - b2( |
_____
Цx2+y2
|
- l)2 = 0. | | |
| |
(4) |
Огибающая семейства овалов Декарта должна
удовлетворять уравнениям дискриминантной кривой [2]:
| F (x, y, j) = 0 и Fj (x, y, j) = 0 | |
при
всевозможных значениях j, 0 Ј
j Ј 2p.
Согласно теории об огибающих семейства
кривых, дискриминантная кривая кроме огибающей содержит геометрическое место
особых точек, которое удовлетворяет уравнениям:
| Fx (x, y, j) = 0 и
Fy(x, y, j) = 0. | |
Продифференцировав уравнение (4), получим
Fx(x,y,j) = 2a2((x - a) + Rcosj) +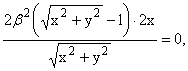 |
|
Fy(x,y,j) = 2a2(y - Rsinj) +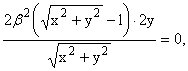 |
|
| Fj(x,y,j) = 2a2R((x - a)sinj - ycosj) = 0. | |
Откуда
следует, что
| x = a + Rcosj,
y = Rsinj и |
tg
|
j = |
y
x - a
|
, | |
sinj =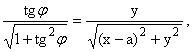
|
|
cosj =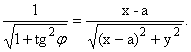
|
| |
Геометрическое место особых точек
представляется уравнением окружности x2+y2=l2;
из полученного результата следует, что
Fx2 + Fy2 №
0.
Исключив j из (4),
получим уравнение огибающей DT(l) семейства овалов
DT(l,j), 0 Ј j Ј 2p,
|
| F(x,y) = a2 |
ж
з
и |
(x - a)2 - 2R |
ж
з
и |
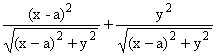
|
|
ц
ч
ш |
+ y2 + R2 |
ц
ч
ш |
- | |
|
- b2 |
ж
и
|
|
_____
Цx2 + y2
|
- l |
ц
ш
|
2
|
= 0, | |
| F(x,y) = a2 |
ж
и
|
(x - a)2 - 2R |
________
Ц(x-a)2+y2
|
+ y2 + R2 |
ц
ш
|
- b2 |
ж
и
|
|
_____
Цx2+y2
|
- l |
ц
ш
|
2
|
= 0, | |
| F(x,y) = a2 |
ж
и
|
|
________
Ц(x-a)2+y2
|
-R |
ц
ш
|
2
|
- b2 |
ж
и
|
|
_____
Цx2+y2
|
-l |
ц
ш
|
2
|
= 0, | | |
| |
| a |
ж
и |
________
Ц(x-a)2+y2
|
- R |
ц
ш |
= b |
ж
и |
|
_____
Цx2+y2
|
-l |
ц
ш |
, | |
Учитывая, что
R = bT, окончательно получаем
Полученное уравнение (5) совпадает с
уравнением (2), откуда следует, что огибающая семейства овалов Декарта
DT(l,j), 0 Ј j Ј 2p,
есть овал Декарта DT(l).
Теорема доказана.
Отметим, что указанный метод нахождения
огибающей для семейства аполлоновых окружностей был использован при решении
задачи определения множества точек встречи, когда преследователь P начинает
преследование с задержкой в случае точечной поимки [3].
Пусть игрок E использует любую
кусочно-постоянную стратегию v [4]. Обозначим через GT(P(0),E(0), l)
множество всевозможных точек встречи, когда P применяет стратегию
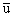 , при различных стратегиях v игрока E. Как известно, при
таких стратегиях (
, при различных стратегиях v игрока E. Как известно, при
таких стратегиях (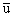 ,v) множество точек встречи
содержится внутри овала Декарта [4].
,v) множество точек встречи
содержится внутри овала Декарта [4].
Таким образом, овал DT(l) является
границей множества GT(P(0),E(0),l).
Следствие. GT(P(0),E(0),l) @ ST(l).
Ереванский научно-исследовательский
институт математических машин
Литература
1. Савелов А.А. Плоские кривые. М. Физматгиз. 1960. 293
с.
2. Рашевский П.К. Курс дифференциальной геометрии. М. Гостехиздат. 1956. 420
с.
3. Амбарян В.С. - ДАН Армении. 1991. Т. 92. N4. С.
147-153.
4. Петросян Л.А.,
Томский Г.В. Геометрия простого преследования. Новосибирск.
Наука. 1983. 143 с.
![]() , a игрок E движется прямолинейно. Тогда геометрическое
место точек встречи описывается следующим уравнением:
, a игрок E движется прямолинейно. Тогда геометрическое
место точек встречи описывается следующим уравнением:
![]() )/(a)] + T = [(
)/(a)] + T = [(![]() )/(b)], обозначим через DT(l), а множество всех точек
внутренней части овала, включая его границу, через ST(l). Семейство
декартовых овалов (3), т.е.
)/(b)], обозначим через DT(l), а множество всех точек
внутренней части овала, включая его границу, через ST(l). Семейство
декартовых овалов (3), т.е. 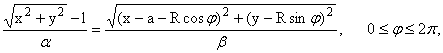
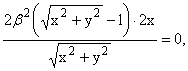
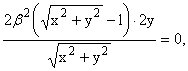
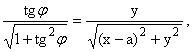
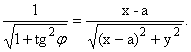
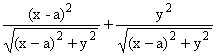
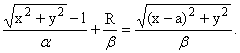
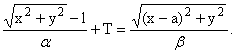
![]() , при различных стратегиях v игрока E. Как известно, при
таких стратегиях (
, при различных стратегиях v игрока E. Как известно, при
таких стратегиях (![]() ,v) множество точек встречи
содержится внутри овала Декарта [4].
,v) множество точек встречи
содержится внутри овала Декарта [4].