МАТЕМАТИКА
УДК 517.53
С.В. Мадоян
Критерии ограниченности и полной ограниченности
множеств в пространствах
N loga
N
(Представлено академиком В.С.Закаряном 16/VI 2003)
1. Введение. Пусть n
О N и Cn = { z = (z1,јzn) : zk О C; 1
Ј k Ј n}. Символом G обозначим
как шар Bn = { z О Cn : |z1|2 + ј + |zn|2 < 1}, так и полидиск Un = { z О Cn : |z1| < 1,ј|zn| < 1}, символом
G - границу Шилова области G, т.е. G есть Sn={ z О
Cn : |z1|2 + ј + |zn|2 = 1} в случае G = Bn и Tn = { z О
Cn : |z1| = 1,ј|zn| = 1} в случае
G = Un. На множестве G существует
вероятностная мера s, совпадающая с нормированной мерой
Лебега на сфере Sn в случае G = Bn и равная прямому
произведению нормированных мер Лебега на единичных окружностях, составляющих тор
Tn, в случае G = Un.
В [1] для произвольного фиксированного числа
a і 1 и функции ja(t) = t · loga(ea + t), t і 0 голоморфная в области G функция f(z) отнесена к классу
Nloga N, если
| |f|a = |
sup
0 Ј r <
1
|
|
у
х
G
|
ja |
ж
и |
log(1 + |f(rg)|) |
ц
ш |
s(dg) < +Ґ, | |
(1) |
и установлено, что Nloga N при каждом a і 1 образуют (F)-пространства относительно метрики ra,
| ra(f,g) = |f - g|a, f,g О Nloga
N | |
(2) |
и поэтому являются
линейно-топологическими пространствами в топологии, порожденной метрикой ra (см., например, [2]
гл. II, § 1, теорема 12). Отметим, что частный случай a
= 1 изучался ранее в [3].
В настоящей статье устанавливаются полные
характеристики ограниченных и вполне ограниченных множеств в пространствах
Nloga N, a і 1. Близкие исследования в одномерном случае n = 1 проведены
для пространства Смирнова N* в [4], а для пространства M - в [5].
В доказательствах результатов этой статьи
потребуются следующие свойства функции ja(t) и метрики ra, установленные в [1]:
1) для произвольного a і 1 и любой функции f О Nloga N справедливо
соотношение
| |f|a = |
у
х
G
|
ja |
ж
и |
log(1 +|f*(g)|) |
ц
ш |
s(dg), | |
(3) |
где f* обозначает функцию
радиальных граничных пределов f,
| f*(g) = |
lim
r®
1
|
f(rg); g
О G; | |
2) для любого l
О C и произвольной функции f(z) из класса
Nloga N, a і 1, справедливы неравенства
|
min
|
(|l|,1)|f|a Ј |lf|a Ј |
max
|
(|l|,1)|f|a; | |
(4) |
3) неравенство
| ja(log(1 + xy)) Ј
2a+1ja(log(1 + x)) + 2a+1ja(log(1 + y)) | |
(5) |
справедливо для всех x і 0 и y і 0 (и a і 1).
2. Ограниченные
множества в пространствах N loga N, a і 1. По определению
подмножество E линейно-топологического пространства T называют ограниченным,
если для любой окрестности V нуля пространства T существует такое число l0 > 0 (зависящее от V, т.е. l0=l0(V)), что
множество lE={lx; x
О E} содержится в V для всех l
О C, |l| < l0 (см., например, [6], гл. III, § 5, п.1).
Теорема 1. Множество A в
(F)-пространстве Nloga N, a і 1, ограничено тогда и только
тогда, когда
a) A ограничено по метрике ra, т.е. существует такая
конечная постоянная K і 0, что |f|a Ј K для всех f О A, и
б) семейство функций {ja(log(1+|f*(g)|)); gОG}fОA имеет равностепенно абсолютно непрерывные
интегралы, т.е. для любого числа e > 0 существует
такое число d > 0, d =
d(e), что
|
у
х
Y
|
ja |
ж
и |
log(1 + |f*(g)|) |
ц
ш |
s(dg) < e | |
для всех
измеримых множеств Y на G с мерой sY < d и всех функций f из
множества A.
Доказательство. Необходимость. Пусть множество A ограничено в
линейно-топологическом пространстве Nloga N,
a і 1.
Чтобы доказать выполнение условия а) теоремы,
рассмотрим в качестве окружности нуля в определении
ограниченности открытый шар V={f О Nloga
N; |f|a < 1} единичного радиуса с
центром в нуле. В силу ограниченности множества A для этой
окружности найдется такое положительное число l0, что для всех l О C, |l| Ј l0 справедливо вложение lA М V, т.е. |lf|a < 1 для всех f
О A. Воспользовавшись неравенствами (4) при l = l0 > 0, имеем
min(1,l0)|fa| Ј |l0 f|a < 1 для всех f О A,
откуда |f|a < max(1,l0-1) = K для
всех f О A.
Для проверки справедливости условия б)
теоремы рассмотрим в качестве окрестностей нуля в пространстве
Nloga N, a і 1, открытые шары
Ve={f О
Nloga N; |f|a < e/2a+2} радиуса e/2a+2 с центром в нуле, где число e > 0 произвольное. В силу ограниченности множества A
существует такое число l0 > 0 (зависящее
от e, l0 = l0(e)), что для всех
l О C, |l| Ј l0 выполнено вложение
lA М Ve, т.е. |lf|a < e/2a+2 для всех f О A. Рассмотрим
произвольное измеримое множество Y на G.
Воспользовавшись указанным выше неравенством (5) и формулой (3), получим оценки
|
| |
у
х
Y
|
ja( log(1 + |f*(g)|))s(dg) Ј 2a+1 |
у
х
Y
|
ja( log(1 + 1/l0))s(dg) + | |
| + 2a+1 |
у
х
Y
|
ja( log(1 + |l0f*(g)|))s(dg) Ј ja( log(1 + 1/l0))sY + 2a+1|l0 f|a <
| |
| < 2a+1ja (1 + 1/l0)sY + |
e
2
|
,
| | |
| |
справедливые для всех
f О A. Поэтому, если мера
| sY < d = |
e
2a+2ja(log(1 + 1/l0))
|
, | |
то
тYja( log(1+|f*(g)|))s(dg) < [(e)/2]+[(e)/2] = e для всех f О A, т.е. выполнено
условие б) теоремы.
Достаточность. Пусть
теперь для множества A (F)-пространства Nloga N, a і 1, выполнены условия а) и б) теоремы. Так как любая
окружность V нуля метрического пространства Nloga N, a і 1, содержит некоторый открытый шар V0
положительного радиуса e0 > 0 с центром в
нуле, т.е. V Й V0={f О Nloga N; |f|a < e0}, то
достаточно проверить определение ограниченности множества A для окружности
V0 нуля в Nloga N, a і 1.
Согласно условию б) теоремы для e0 > 0 существует такое d0 > 0, что
|
у
х
Y
|
ja(log(1 + |f*(g)|) )s(dg) < |
e
2
|
| |
(6) |
для любого измеримого на G множества Y с мерой sY < d0 и произвольной функции f О A. Согласно условию а) теоремы существует такая конечная
постоянная K і 0, что |f|a Ј K для всех f О A, так что, по
неравенству Чебышева, для множеств Yn
(f) = {g О G; |f*(g) і n},
n О N, f О A, справедлива оценка
| sYn(f) Ј |
1
ja(log(1 + n))
|
|
у
х
G
|
ja( log(1 + |f*(g)|))s(dg) Ј |
K
ja(log(1 + n))
|
, | |
в
которой использована также формула (3). Следовательно, найдется такое
натуральное число n0, что все множества
Yn0(f), f О A, имеют меру меньшую d0, и поэтому в неравенстве (6) можно положить
Y=Yn0(f). Тогда для произвольного
l О C, |l| Ј 1 и любой функции f О A получим
|
| |lf|a = |
у
х
G
|
ja(log(1 + |lf*(g)|))s(dg) Ј |
у
х
Yn0(f)
|
ja(log(1 + |f*(g)|))s(dg) + | |
| + |
у
х
G\Yn0(f)
|
ja(log(1 + |l||f*(g)|))s(dg) <
|
e0
2
|
+ ja(log(1 + |l|n0)). | | |
| |
Выбирая l0 = l0(e0) > 0 таким образом, чтобы были выполнены
неравенства l0 Ј 1
и ja(log(1+l0n0)) Ј e0/2, заключаем, что
для любой функции f О A и любого l О C, |l| Ј l0, выполнено
неравенство |lf|a < [(e0)/2]+[(e0)/2]=e0,
т.е. lA М V0 М V и множество A ограничено в линейно-топологическом
пространстве Nloga N, a Ј 1.
Укажем стандартный пример ограниченного
множества в Nloga N, a Ј 1. Рассмотрим произвольную
функцию f О Nloga N
и функцию fr, 0 Ј r < 1, определяемые
формулой fr(z) = f(rz), z О G. Тогда множество
{ f}0 Ј r < 1 ограничено в Nloga N, поскольку условие а) теоремы 1 выполнено в силу
принадлежности функции f классу Nloga N (см.
формулу (1)), а условие б) есть не что иное, как пункт 6) утверждения 1 статьи
[1].
3. Вполне
ограниченные множества в пространствах N loga
N, a і 1. Понятие
полной ограниченности множества можно трактовать разными способами (см. [2-7]).
Однако в полных метрических пространствах (а пространство Nloga N, a Ј 1, таковым в метрике ra является на основании результатов статьи [1])
свойство полной ограниченности множества равносильно свойству его относительной
компактности, т.е. тому, что из любой последовательности элементов множества
можно выделить сходящуюся подпоследовательность (см. например [6], гл. II, §7,
теорема 3).
Теорема 2. Множество B
М Nloga N, a і 1, вполне ограничено в
пространстве Nloga N тогда и только тогда,
когда
а) B ограничено в Nloga N (как в линейно-топологическом пространстве), и
б) семейство функции { f*(g);g О
G}f О B относительно компактно в топологии сходимости по мере s
на G.
Доказательство. Необходимость. Пусть множество B вполне ограничено в
линейно-топологическом пространстве Nloga N,
a і 1. Поскольку утверждение
об ограниченности вполне ограниченных множеств является общим результатом теории
линейно-топологических пространств (см. например [8], гл. 2, § 7, п. 5), то
условие а) теоремы выполнено.
Для проверки выполнения условия б) теоремы
рассмотрим произвольную последовательность (gn) функции семейства { f*(g);g О
G}f О B. Тогда, по
определению этого семейства, существует такая последовательность функций
(fn) в множестве B, что
 = gn почти всюду на G для каждого
n О N. Вполне ограниченное
множество B относительно компактно в Nloga
N, и, следовательно, из последовательности (fn) можно выделить подпоследовательность (fnk), nk+1 > nk,
k О N, сходящуюся к некоторой функции f О Nloga N по метрике
ra. Согласно
неравенству Чебышева и формуле для |f|a в свойстве 1)
= gn почти всюду на G для каждого
n О N. Вполне ограниченное
множество B относительно компактно в Nloga
N, и, следовательно, из последовательности (fn) можно выделить подпоследовательность (fnk), nk+1 > nk,
k О N, сходящуюся к некоторой функции f О Nloga N по метрике
ra. Согласно
неравенству Чебышева и формуле для |f|a в свойстве 1)
s{ g О G; |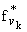 (g) - (g) -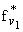 (g)| і e} Ј (g)| і e} Ј |
|fnk-fnl|
ja(log(1 + e))
|
® 0 при k,l ® Ґ | |
при
каждом фиксированном e > 0, т.е.
подпоследовательность (gnk) = (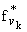 ) фундаментальна по мере s. Таким образом, из любой последовательности функций
семейства { f*(g); g О G}f О B мoжно выделить
фундаментальную по мере s подпоследовательность, и, так
как метрика сходимости по мере s полна, то семейство {
f*(g); g
О G}f О B относительно компактно и свойство б) установлено.
) фундаментальна по мере s. Таким образом, из любой последовательности функций
семейства { f*(g); g О G}f О B мoжно выделить
фундаментальную по мере s подпоследовательность, и, так
как метрика сходимости по мере s полна, то семейство {
f*(g); g
О G}f О B относительно компактно и свойство б) установлено.
Достаточность.
Пусть множество B пространства Nloga N удовлетворяет условиям а) и б) теоремы; рассмотрим
произвольную последовательность (fn) функции
fn О B, n О N. Так как измеримые на G функции fn, n О N, содержатся в семействе {
f*(g); g
О G}f О B, то согласно условию б) существует
подпоследовательность
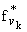 , сходящаяся по мере s к некоторой измеримой на G функции
g. По теореме Ф. Рисса, в (
, сходящаяся по мере s к некоторой измеримой на G функции
g. По теореме Ф. Рисса, в (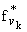 ) существует подпоследовательность
(
) существует подпоследовательность
(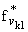 ), сходящаяся к
g почти всюду на G. Обозначим
), сходящаяся к
g почти всюду на G. Обозначим
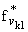 l=
l=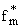 , l О N; m О N. Согласно условию а)
доказываемой теоремы и условию а) теоремы 1 существует такая конечная постоянная
K і 0, что
, l О N; m О N. Согласно условию а)
доказываемой теоремы и условию а) теоремы 1 существует такая конечная постоянная
K і 0, что
|
у
х
G
|
ja(log(1 + |fm*(g)|))s(dg) Ј K | |
для
всех m О N, переходя к пределу при m ® +Ґ, с учетом леммы Фату - Лебега
получим
|
у
х
G
|
ja(log(1 + |g(g)|))s(dg) Ј K, | |
т.е.
функция ja(log(1+|g|)) интегрируема по s на G. В силу условия б) теоремы 1 последовательность {ja(log(1+|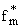 |))} имеет
равностепенно абсолютно непрерывные интегралы, что вместе с уже доказанным
свойством интегрируемости функции ja(log(1+|g|)) влечет равностепенную абсолютную непрерывность интегралов
последовательности {ja(log(1+|
|))} имеет
равностепенно абсолютно непрерывные интегралы, что вместе с уже доказанным
свойством интегрируемости функции ja(log(1+|g|)) влечет равностепенную абсолютную непрерывность интегралов
последовательности {ja(log(1+|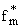 -g|))}, поскольку согласно элементарному неравенству
-g|))}, поскольку согласно элементарному неравенству
| ja(log(1 + |x - y|)) Ј ja(log(1 + |x|)) + ja(log(1 + |y|)) | |
(7) |
(см.[1]) выполнено
ja(log(1 + |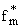 - g|)) Ј ja(log(1 + | - g|)) Ј ja(log(1 + |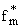 |)) + ja(log(1 + |g|)). |)) + ja(log(1 + |g|)). | |
Поэтому для последовательности {ja(log(1 +
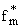 - g|))} выполнены все условия общей предельной теоремы (см. [6],
с. 28), на основании которой заключаем, что
- g|))} выполнены все условия общей предельной теоремы (см. [6],
с. 28), на основании которой заключаем, что
|
у
х
G
|
ja(log(1 + |fm*(g) - g(g)|))s(dg) ® 0 при m ® +Ґ, | |
и,
применяя неравенство (7), получим, что
| |fm - fp|a = |
у
х
G
|
ja(log(1 + |fm*(g) - fp*|))s(dg) ®
0 | |
при m,p ® +Ґ, т.е. что подпоследовательность
(fm) = (fVkl) фундаментальна. Итак, любая
последовательность функций множества B содержит фундаментальную
подпоследовательность и множество B вполне ограничено в пространстве
Nloga N, a і 1.
Рассмотренное в предыдущем пункте
ограниченное в пространстве Nloga N, a і 1, множество
{fr}0 Ј r < 1,
порожденное произвольной функцией f О
Nloga N, a і 1, по формуле fr(z) = f(rz), z О G, 0 Ј r < 1, предоставляет
также пример вполне ограниченного множества в Nloga N, a і 1. Действительно, справедливость условия а) теоремы 2 для
множества { fr}0 Ј r < 1
доказана в предыдущем пункте. Чтобы проверить выполнение условия б) теоремы 2,
рассмотрим произвольную последовательность
{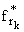 }, 0 Ј
rk < 1, k О N и заметим, что
}, 0 Ј
rk < 1, k О N и заметим, что
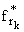 (g) = f(rkg), g О G, k
О N. Если последовательность rk имеет
предельную точку внутри промежутка [0,1), скажем r0, 0 Ј r0 < 1, то в силу равномерной непрерывности
функции f на компактах внутри G последовательность (frk)
сходится на G к функции fr0
равномерно, и следовательно, и по мере s. Если же
rk ® 1 при k ® Ґ, то (frk) сходится к f*
почти всюду на G, а значит, и по мере s. Таким образом, в обоих случаях множество
{fr}0 Ј r < 1 удовлетворяет
условию б) теоремы 2 и поэтому вполне ограниченно в Nloga N, a і 1.
(g) = f(rkg), g О G, k
О N. Если последовательность rk имеет
предельную точку внутри промежутка [0,1), скажем r0, 0 Ј r0 < 1, то в силу равномерной непрерывности
функции f на компактах внутри G последовательность (frk)
сходится на G к функции fr0
равномерно, и следовательно, и по мере s. Если же
rk ® 1 при k ® Ґ, то (frk) сходится к f*
почти всюду на G, а значит, и по мере s. Таким образом, в обоих случаях множество
{fr}0 Ј r < 1 удовлетворяет
условию б) теоремы 2 и поэтому вполне ограниченно в Nloga N, a і 1.
Государственный инженерный университет
Армении
Литература
1.
 -
-
2. Dunford N., Schwarts J.
T. Liner Operators. Part I. General Theory. Interscince
Publishers. New York. 1958. (Рус. пер. Н. Данфорд, Дж. Шварц. Линейные
операторы. Общая теория. М. ИЛ. 1962. 896
с.)
3. Гаврилов В.И.,Субботин
А.В. - Матер. конф.: Вопр. функц. анализа и мат. физики.
Баку. Чашыоглу. 1999. С. 240-251.
4. Yanagahara N. - Sci. Papers College Gen. Ed. Univ.
Tokyo. 1973. V. 23.
5. Hong
Oh Kim. - Can. J. Math. 1988. V. 40. N 3. P.
718-741.
6. Колмогоров А.Н.,
Фомин С. В. Элементы теории функций и функционального
анализа. М. Наука. 1981. С. 544.
7. Meyer P.A. Probability and potentials. Blaisdell
publishing company. English translayed. Whaltham. Massachusets-Toronto-London.
1965. (Рус. пер. П.А. Мейер. Вероятность и потенциалы. М. Мир. 1973. 328
с.).
8. Kelley J.L., Namioka I.
et al Liner Topologikal spaces. D. Van Nostrand Company.
Inc. Princetion. New Jersy-Toronto-New York-London. 1963.
![]() = gn почти всюду на G для каждого
n О N. Вполне ограниченное
множество B относительно компактно в Nloga
N, и, следовательно, из последовательности (fn) можно выделить подпоследовательность (fnk), nk+1 > nk,
k О N, сходящуюся к некоторой функции f О Nloga N по метрике
ra. Согласно
неравенству Чебышева и формуле для |f|a в свойстве 1)
= gn почти всюду на G для каждого
n О N. Вполне ограниченное
множество B относительно компактно в Nloga
N, и, следовательно, из последовательности (fn) можно выделить подпоследовательность (fnk), nk+1 > nk,
k О N, сходящуюся к некоторой функции f О Nloga N по метрике
ra. Согласно
неравенству Чебышева и формуле для |f|a в свойстве 1) ![]() ) фундаментальна по мере s. Таким образом, из любой последовательности функций
семейства { f*(g); g О G}f О B мoжно выделить
фундаментальную по мере s подпоследовательность, и, так
как метрика сходимости по мере s полна, то семейство {
f*(g); g
О G}f О B относительно компактно и свойство б) установлено.
) фундаментальна по мере s. Таким образом, из любой последовательности функций
семейства { f*(g); g О G}f О B мoжно выделить
фундаментальную по мере s подпоследовательность, и, так
как метрика сходимости по мере s полна, то семейство {
f*(g); g
О G}f О B относительно компактно и свойство б) установлено.![]() , сходящаяся по мере s к некоторой измеримой на G функции
g. По теореме Ф. Рисса, в (
, сходящаяся по мере s к некоторой измеримой на G функции
g. По теореме Ф. Рисса, в (![]() ) существует подпоследовательность
(
) существует подпоследовательность
(![]() ), сходящаяся к
g почти всюду на G. Обозначим
), сходящаяся к
g почти всюду на G. Обозначим
![]() l=
l=![]() , l О N; m О N. Согласно условию а)
доказываемой теоремы и условию а) теоремы 1 существует такая конечная постоянная
K і 0, что
, l О N; m О N. Согласно условию а)
доказываемой теоремы и условию а) теоремы 1 существует такая конечная постоянная
K і 0, что ![]() |))} имеет
равностепенно абсолютно непрерывные интегралы, что вместе с уже доказанным
свойством интегрируемости функции ja(log(1+|g|)) влечет равностепенную абсолютную непрерывность интегралов
последовательности {ja(log(1+|
|))} имеет
равностепенно абсолютно непрерывные интегралы, что вместе с уже доказанным
свойством интегрируемости функции ja(log(1+|g|)) влечет равностепенную абсолютную непрерывность интегралов
последовательности {ja(log(1+|![]() -g|))}, поскольку согласно элементарному неравенству
-g|))}, поскольку согласно элементарному неравенству ![]() - g|))} выполнены все условия общей предельной теоремы (см. [6],
с. 28), на основании которой заключаем, что
- g|))} выполнены все условия общей предельной теоремы (см. [6],
с. 28), на основании которой заключаем, что ![]() }, 0 Ј
rk < 1, k О N и заметим, что
}, 0 Ј
rk < 1, k О N и заметим, что
![]() (g) = f(rkg), g О G, k
О N. Если последовательность rk имеет
предельную точку внутри промежутка [0,1), скажем r0, 0 Ј r0 < 1, то в силу равномерной непрерывности
функции f на компактах внутри G последовательность (frk)
сходится на G к функции fr0
равномерно, и следовательно, и по мере s. Если же
rk ® 1 при k ® Ґ, то (frk) сходится к f*
почти всюду на G, а значит, и по мере s. Таким образом, в обоих случаях множество
{fr}0 Ј r < 1 удовлетворяет
условию б) теоремы 2 и поэтому вполне ограниченно в Nloga N, a і 1.
(g) = f(rkg), g О G, k
О N. Если последовательность rk имеет
предельную точку внутри промежутка [0,1), скажем r0, 0 Ј r0 < 1, то в силу равномерной непрерывности
функции f на компактах внутри G последовательность (frk)
сходится на G к функции fr0
равномерно, и следовательно, и по мере s. Если же
rk ® 1 при k ® Ґ, то (frk) сходится к f*
почти всюду на G, а значит, и по мере s. Таким образом, в обоих случаях множество
{fr}0 Ј r < 1 удовлетворяет
условию б) теоремы 2 и поэтому вполне ограниченно в Nloga N, a і 1.