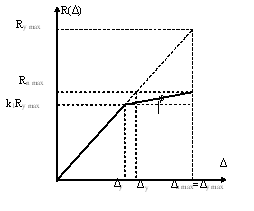
As
shown on the figure 1 it takes place
|
Dn max
Dy¢
|
= |
Ry max
Rn max
|
. | |
(2) |
Figure 1.
To definition of coefficient of
damages.
For the ideal elastic-plastic materials
(structures) Dy = Dy¢ and as
result will have
| Rn max = |
Ry max
m
|
, or
Rn max = k1Ry max, | |
(3) |
where is
| k1 = |
1
m
|
= |
Rn max
Ry max
|
. | |
(4) |
Thus, the coefficient of damages
k1 represents the relation of elastic-plastic response of system in
the moment of beginning of plastic deformation Rn max to
conventional maximal response Ry max of this system in the
assumption of its elastic behavior from beginning to end of earthquake.
The non-elastic deformation in the buildings
and structures always arise during the strong earthquake. The study of these
deformations under the accelerograms of strong earthquakes for the different
"regeneration force - relative movement" non-linear relations is shown one
important property of the process of structure deformation: maximal displacement
of the elastic and non-elastic structures with the same equivalent natural
periods of free oscillation and damping characteristics very closed when the
value of das not exceed 3-4 [1,2,3]. In the table 1 are shown the calculation
results for simple system with one degree of freedom for elastic and equivalent
non-elastic system under the different values of k1 [3] under the
accelerogram of real earthquake (the maximal ground acceleration is 0.25g,
Eureka Earthquake, 21.12.1954), which are confirm above mentioned.
Table 1
The value of maximal displacements
|
The value of initial period of free
oscillation, T, sec |
Maximal displacement, cm |
Elastic calculation
|
Non-elastic calculation |
|
m=1.43
k1=0.7 |
m=2.0
k1=0.5 |
m=3.33
k1=0.3 |
|
0.35 |
2.41 |
2.37 |
1.99 |
2.89 |
|
0.4 |
2.97 |
3.91 |
3.67 |
2.94 |
|
0.45 |
3.97 |
3.87 |
4.14 |
2.86 |
|
0.5 |
4.27 |
4.18 |
3.41 |
3.83 |
|
0.55 |
3.01 |
3.45 |
3.81 |
3.99 |
|
0.6 |
5.53 |
5.34 |
5.04 |
6.6 |
|
0.7 |
6.05 |
4.98 |
6.33 |
4.54 |
|
0.8 |
4.57 |
4.02 |
3.40 |
4.83 |
|
1.0 |
3.86 |
3.44 |
3.91 |
4.10 |
|
1.2 |
2.96 |
3.61 |
4.99 |
3.28 |
|
1.5 |
8.04 |
8.55 |
7.67 |
7.12 |
|
2.0 |
14.3 |
14.4 |
14.0 |
13.9 |
|
2.5 |
17.2 |
18.0 |
19.8 |
11.3 |
|
3.0 |
18.5 |
18.6 |
15.7 |
12.7 |
|
The same results were received for the 10
storeys reinforced concrete frame building with masses
m1 = m2 = ...m10 = 52kgsec2/cm, storeys
stiffness a1 = a2 = ...an = 110400kg/cm and
k1 = 0.5, jk = 0;0.2;0.5 under the
calculation by accelerogram of Holister Earthquake (09.03.1949, maximal ground
acceleration was 0.125g). The results of this calculation are shown in figure 2.
2. Criterion of seismic
resistance for calculation by the Armenian Codes. The formation of
damages in reality is the cause of decreasing the stiffness of structure,
increasing the its period of natural oscillation and arising of residual
deformation. The optimum design solution is the compromise of two approaches:
decreasing of stiffness (through including the coefficient k1) and
limitation of displacements (elastic + elastic-plastic).
Figure.2 Distributing of
displacements for elastic and non-elastic calculations
of 10 storeys building.
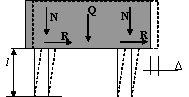
On the sample of system with one degree of freedom - one floor frame
with rigid beam, carrying the concentrated load Q (figure 3) will show the
conditions when it is possible to have above-mentioned compromise for design by
the Armenian Norm CCRA II-2.02-94 [4].
Figure 3. Deformation scheme of structure
According to code [4] the elastic seismic load for the one floor
structure for the I-st category of soil and periods T ³
0.4 sec will be
where is
is horizontal acceleration of
concentrated mass Q/g.
Because of between concentrated mass and its
displacement there is relation [3]:
| t(T) = |
æ
ç
è |
|
2p
T
|
|
ö
÷
ø |
2
|
y(T) | |
(7) |
for displacement of system by norm
CCRA II-2.02-94
| y(T) = |
tT2
(2p)2
|
= |
1.35Agk0T2
(2p)2T2/3
|
. | |
If
will take into consideration the seismic zone 3 (A=0.4) and taking
k0=0.8 for I-st category of soil for maximal displacements under the
elastic oscillation will have
The
period of natural oscillations for the structural system (column with fixed
edges), which is shown on the figure 2, will have
|

|
(9) |
Transfer (9) to (8) and assuming
where is s
normal stress in the columns under the permanent loading for the displacement
(8) will have (in the cm)
| ymax = 1.27s2/3h-4/3l2E-2/3. | |
(11) |
Thus we can take into consideration that during the earthquakes the
expression (11) for the maximal displacements of structure for the conventional
elastic and real elastic-plastic behavior is the same, where s is normal stress in the column, E - initial module of
elasticity, h -column cross section height and l - column height.
For the optimal design it is necessary to
determine by the experiment the value of very important parameter: what
displacement limitation may be allow or the structure.
J. F. Borjes and A.Ravara have shown [2] on
the base of experimental studying of reinforced concrete elements buckling and
on the base of hypothesis of plane section and ideal diagram ßtress-deformation"
for concrete and reinforcement (maximal relative deformation 1% for the strained
reinforcement and 0.35% for the concrete correspond to destruction) and
non-elastic behavior, that for the fixed by two edges column the boundary
displacement express in the following way
where are n = [N/(bhsbk)], sbk -
characteristically strength of cylindrical concrete samples with age 28 days,
which is assume equal to 85% of cubic strength. The percentage of reinforcement
of samples was in limitation 0.5-1.5%, and value of yielding coefficient equal
m = 3.5. By the mean of authors [2], at the more large
percentages of reinforcement the value of yielding coefficient may be too high.
As authors mention the expression (12) may be true for different classes of
concrete and steel.
Base on the main criterions of seismic
resistance - the maximal movement of structure with taking into consideration of
elastic-plastic deformation can't exceed permissible value:
On
the base of (11) and (12) will have:
| 1.27s2/3h-4/3l2E-2/3 < 2×10-4 |
sbk
sh
|
l2. | |
(14) |
From where
| slim
< 5.23×10-3sbk3/5E2/5h1/5. | |
(14¢) |
The
expression (14) allows determine relation between the height of cross section h
and minimal value of axial stress s under the permanent
loading for the column with known concrete class (strength). On the case of
keeping of this relation the value of yielding of structure m may be take equal 3.5 (k1=0.285).
3. Analysis of results.
In the table 2 are shown boundary values of axial stresses slim lim what were calculated
by (14) in dependence of column cross section h for the light and heavy concrete
which are usually use in the construction of frame buildings in Armenia
(concrete class B15, B20 and B25).
Table 2
The limit values of axial stresses
|
Height of column cross section h, cm |
Limit values of axial stress
slim
under the permanent loading for the different concretes, kgf/cm2 |
|
light concrete |
heavy concrete |
|
B15
D2000 |
B20
D1800 |
B20
D2000 |
B25
D2000 |
B15 |
B20 |
B25 |
|
20 |
24.3 |
32.5 |
34.4 |
39.5 |
26.8 |
39.2 |
45.6 |
|
30 |
26.4 |
35.3 |
37.3 |
42.8 |
29.1 |
42.5 |
49.5 |
|
40 |
27.9 |
37.4 |
39.5 |
45.4 |
30.8 |
45.0 |
52.4 |
|
50 |
29.2 |
39.1 |
41.3 |
47.4 |
32.2 |
47.1 |
54.8 |
|
60 |
30.3 |
40.5 |
42.9 |
49.2 |
33.4 |
48.8 |
56.8 |
|
70 |
31.2 |
41.8 |
44.3 |
50.7 |
34.5 |
50.3 |
58.6 |
|
80 |
32.1 |
42.9 |
45.4 |
52.1 |
35.4 |
51.7 |
60.2 |
|
The values of characteristically strength of
concrete sbk correspondingly take equal 200,
250, and 300kgf/cm2. For the light concrete were considered three
class of concrete: B20 (D1800), B20 (D2000) and B25 (D2000) with initial module
of elasticity E equal 173×103, 199×103 and
214×103 kgf/cm2 correspondingly. For the heavy concrete
class B15, B20 and B25 the values of initial modules of elasticity were
235×103, 275×103 and 306×103 kgf/cm2
correspondingly [5].
As you can see from Table 2, with increasing
of column cross section height h the value of boundary axial stress under the
permanent loading also increase, but very slowly. For the column from light
concrete at h=30¸50cm the value of slim is 13¸15% from sbk and at
h=60¸80cm - 15¸16% from sbk. For the column from heavy concrete these
relation is insignificant higher and there are at h=30¸50cm - 15¸19% from sbk and at h=60¸80cm -
18¸21% from sbk.
The limitation of relative drifr of stories
D of buildings also can be considers as measure for the
structure seismic resistance. According to Armenian Code CCRA II-2.02-94 for the
frame reinforced concrete structures this limitation is 1/200 of the building
height [4]. With accordance to experimental results what were received by M.
Melkumyan [6] for the P-type reinforced concrete frame
the limit drift D may be assume a 1/200¸1/160 of the floor height. In accordance to [2] the relative
displacement for the buildings with ordinary height of the floors cannot exceed
2cm, that is for floor height l = 300cm corresponded to D
= l/150.
On the base of (11), the drift limitation can
be express by the following way
| 1.27s2/3h-4/3l2E-2/3 < D. | |
(15) |
From (15) it is possible to determine the minimal height of column cross
section for the different values of axial stresses s:
| h > 1.196s1/2E-1/2D-3/4l3/2. | |
(16) |
For
the above considered columns from the light and heavy concrete B15, B20 and B25
classes the minimal values of h calculated by (16) for the two values of limit
drift D = 1.5 cm (l/200) and D
= 2.0cm (l/150) are shown in the table 3.
Table 3
The minimal values of columns section height h
|
Normal stress in the column under the
permanent loading
s,
kgf/cm2 |
The height of column h must be
not less than (cm) |
|
acceptable drift is
D=1.5cm |
acceptable drift is
D=2.0cm |
|
ight concrete |
heavy concrete |
light concrete |
heavy concrete |
|
B20 D1800 |
B20 D200 |
B25 D200 |
B15 |
B20 |
B25 |
B20 D1800 |
B20 D200 |
B25 D200 |
B15 |
B20 |
B25 |
|
5 |
25 |
23 |
22 |
21 |
20 |
18 |
20 |
19 |
18 |
17 |
16 |
15 |
|
10 |
35 |
33 |
31 |
30 |
28 |
26 |
28 |
26 |
25 |
24 |
22 |
21 |
|
15 |
43 |
40 |
38 |
37 |
34 |
32 |
34 |
32 |
31 |
29 |
27 |
26 |
|
20 |
49 |
46 |
44 |
42 |
39 |
37 |
40 |
37 |
35 |
34 |
31 |
30 |
|
25 |
55 |
51 |
49 |
47 |
44 |
41 |
44 |
41 |
39 |
38 |
35 |
33 |
|
30 |
60 |
56 |
54 |
52 |
48 |
45 |
47 |
45 |
43 |
42 |
38 |
36 |
|
35 |
65 |
61 |
59 |
56 |
52 |
49 |
52 |
49 |
46 |
45 |
42 |
40 |
|
40 |
69 |
65 |
63 |
60 |
55 |
52 |
56 |
52 |
51 |
48 |
44 |
42 |
|
45 |
74 |
69 |
66 |
63 |
59 |
55 |
59 |
56 |
53 |
51 |
47 |
44 |
|
50 |
79 |
73 |
70 |
67 |
62 |
58 |
63 |
58 |
56 |
54 |
50 |
47 |
|
55 |
82 |
76 |
73 |
70 |
65 |
61 |
66 |
61 |
59 |
56 |
52 |
49 |
|
60 |
85 |
80 |
77 |
73 |
68 |
64 |
69 |
64 |
62 |
59 |
54 |
52 |
|
70 |
92 |
86 |
83 |
79 |
73 |
69 |
74 |
69 |
67 |
64 |
56 |
56 |
|
80 |
98 |
92 |
87 |
85 |
78 |
74 |
79 |
74 |
70 |
68 |
60 |
60 |
|
As shown in table 3 the minimal height of the
columns cross-section at D = 2cm in 1.24 times less
than the acceptable distortion D = 1.5cm. The
comparison of the data of tables 2 and 3 shown the significant differences
between limit maximal axial stresses and minimal heights of columns sections for
the limit drift calculated by formula (15) and deformations by formula (12). The
values of axial stresses s for the small and large height of columns section
change insignificantly when use the formula (12) and when use the formula (15)
this change is more rapidly. But in real limitation of column cross section
height 50 < h < 70cm the using of both formula give the same result.
4. Conclusion. The research shows the connections
between the coefficient of damaged, floors acceptable drifts, axial stresses and
cross section height of reinforced concrete columns. In the research it is
shown:
1) for the ordinary dimensions of cross section of columns (from 40 cm to 80
cm) and at the coefficient of damages k £ 0.3 the
values of axial stresses under the permanent loading can not be more than 25%
from characteristically strength of concrete;
2) the minimal height of column cross section at the acceptable drift D = 2.0cm in the 1.24 times less than at D = 1.5cm;
3) the minimal height of cross section of column from heavy concrete is in
the 1.5 times less than light concrete when the class of concrete is the same.
The main conclusion of research is that for
the ordinary dimensions of columns cross sections the axial forces must be
limited and its values must be not more than 25% from characteristically
strength of concrete.
Above were shown the analysis of simple
system with one degree of freedom. As shown in [2,3,9] and many other works, the
maximal displacements in the elastic and elastic-plastic calculations of
multi-storey buildings also insignificantly different like it is for above
mentioned single floor buildings. In this case it is only necessary to increase
the maximal displacement (8) on 20-25%. Therefore above-mentioned conclusions
can be the same for ground floors of multi-storey buildings.
The selective calculations by norms of the
former USSR (k1=0.24, A=0.1-0.2g) of axial
stresses under the permanent loadings for existing in Armenia multi-storey frame
buildings shown that they don't satisfy to above-mentioned conditions. It is
significantly decrease their real yielding and increase the possibility of
brittle destruction during the earthquakes with ground acceleration 0.3-0.4g,
that foreseen by Armenian Codes.
Yerevan State University of Architecture and
Construction
References
1. Newmark N.M., Rosenblueth E. Fundamentals of Earthquake Engineering, (Prentice-Hall,
Inc.Englewood CCliffs, N.Y., 1971) translation on Russian, M., p.344,
1980.
2. Borges I. F., Ravara
A. Earthquake Engineering Seismic Design of Reinforced Concrete
Buildings, (Lisbon, 1969) translation on Russian, M., p.136,
1978.
3. Khachian E. E. Seismic Impact on High Buildings and Structures, Hayastan, Yerevan,
p.328, 1973. (in Russian)
4. Seismic
Construction. Construction Codes of Republic of Armenia CCRA II-2.02-94 Yerevan, p.94, 1998. (in Armenian and Russian)
5. Concrete and Reinforced Concrete Structures. Construction Codes
CCR 2.03.01-84 Moscow, p.79, 1985. (in
Russian)
6. Melkumyan M. G. Forming of Dynamic Calculation Models for Seismic Response
Analysis of Reinforced Concrete Buildings, Yerevan, p.100, 1993. (in
Russian)
7. Poltavtsev S. I.,
Ayzenberg Y. M., Koff G. L., Melentiev A. M.- Seismic Zonning and
Seismic Construction, Moscow, p.260, 1998. (in Russian)
8. Construction in the Seismic Regions. Construction Codes CCR
II-7-81 Moscow, p.47, 1982. (in
Russian)
9. Clough R. W,
Penzien I. - Dynamics of Structures, (McGraw-Hill Book Company,
New-York, 1975) translation on Russian, Moscow, p.320, 1979.