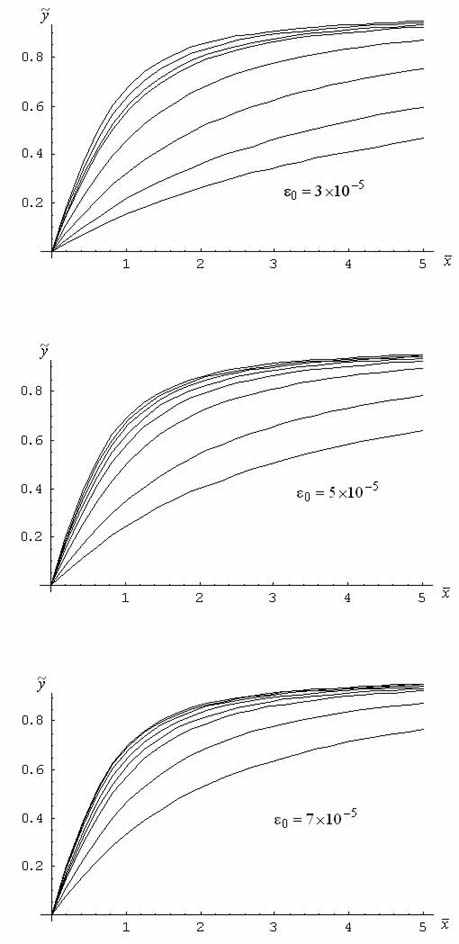
М a, км a, 1/км 5       3 0.986 0.2 4.85 4.15 1.17 5.6 0.95 0.333 4.49 7 0.64 6.1 0.885 0.5 4.37 12.5 0.349 6.7 0.85 0.9 1.61 22 0.073 7.2 0.76 1.2 1.27 37.5 0.034 7.8 0 1.8 1.22 65 0.02 8.4 0 2.8 0.4034 115 0.00351 8.9 0 3.2 0.30237 205 0.00148   5       5 0.996 0.2 5,9 4.15 1.42 5.6 0.984 0.333 5.27 7 0.75 6.1 0.976 0.5 3.4 12.5 0.272 6.7 0.958 0.9 1.79 22 0.081 7.2 0.93 1.2 1.42 37.5 0.038 7.8 0.87 1.8 0.99 65 0.015 8.4 0.6 2.8 0.87 115 0.0076 8.9 0.4 3.2 0.85 205 0.0041    5       7 0.999 0.2 16.68 4.15 4.02 5.6 0.99 0.333 6.95 7 0.99 6.1 0.978 0.5 6.15 12.5 0.492 6.7 0.97 0.9 2.54 22 0.12 7.2 0.96 1.2 1.95 37.5 0.052 7.8 0.93 1.8 1.26 65 0.02 8.4 0.8 2.8 1.08 115 0.0094 8.9 0.75 3.2 0.97 205 0.0047

  где U есть компонента перемещения по оси x,a₀ и b есть скорости продольных и поперечных упругих волн.
   Следуя [1], найдем деформацию на разломе в виде e = [(¶V)/(¶x)]+[(¶U)/(¶y)], e(y,0) = e₀,

где введены безразмерные величины = [y/a], = aa, = [(y^ў)/a].
   Можно показать, используя ветвь арктангенса arctg(-x) = p-arctgx, что (2) удовлетворяет условиям (1).
   Поскольку для типичных землетрясений значения минимальной деформации на разрыв известны [4,5], а именно e₀ = 3 · 10^-5;  5 · 10^-5; 7 · 10^-5, можно задавать [(V₀)/2a]u из (3) найти параметр a закладки данного землетрясения. При этом, в отличие от [4], a зависит также от координаты y = y_min, начиная с которой возможен разрыв. В [1] это значение y_min для заданного землетрясения находится из упрощенного уравнения (3), записанного для больших   из требования, чтобы в окрестности y = y_min кривая (y) была медленно меняющейся. В настоящей работе это требование сохраняется, но применяется оно к точному уравнению (3).
   В результате получаются значения и a, которые качественно, но не количественно согласуются с данными [1,4] и приведены в таблице.
   По ориентировочным данным или a = [()/a] из таблицы можно построить графики функции V(0,x) для разных [(V₀)/2a],  a, a и путем сравнения с предполагаемыми опытными данными найти a для данного землетрясения, a магнитуду (m) определить по таблице или по известным формулам [3-8]. Эти кривые приведены на рисунке, где = [x/a]. При этом верхние кривые соответствуют большим значениям , взятым из таблицы. Другие методы предсказания землетрясений рассмотрены в [6-8].
   Предположим теперь, что значения меняются от года к году и определим время, прошедшее с начала подготовки землетрясения. Пусть t₀ есть данный момент времени, например t₀ = 2003 год. По измерениям на местности, приведенным выше, которые сравниваются с данными рисунка, найдем значения ₁, ₂, ₃ при t = t₀, t = t₀+1, t = t₀+2.
   Уравнение прямой регресcии

= At + B.

(4)

Постоянные A и B находятся из минимума величины

y = (At0 + B -1 )2 + (At0 + A + B -2 )2 + (At0 + 2A + B -3 )2

(5)

в виде

A = -,   A < 0,   B = -At0 - A +

(6)

   Проведем прямую (4) плоскости t, и обозначим через t = b значение начала закладки процесса.
   В качестве естественного предположения считаем, что для всех видов землетрясений, для которых _1,2,3 находятся для моментов t₀,  t₀ + 1 и t₀ + 2 указанным выше способом, начальные значения (b) = a⁰ одинaковы.
   Пусть для одного землетрясения значение момента закладки b₀ известно. Тогда по нему из (4) можно найти a⁰, а начальные значения t = b для остальных строк найдутся подстановкой = a⁰ в (4), где значения A и B находятся по (6) для каждых _1,2,3 и t₀. Тогда t₀ - b даст время, прошедшее с момента закладки процесса для данного района
Автор благодарит А. В. Саакяна, проделавшего все расчеты по таблицe и графикам.

   Институт механики НАН РА

Литература

   1. Мовсесян Р. А., Багдоев А. Г., Саакян А. В.- ДНАН Армении. 2002. Т.102. №2. С. 153-158.
   2. Мкртчян М. С., Хачикян А. С.- Изв. НАН Армении. Механика. 1995. Т. 48. №1. С. 16-23.
   3. Аки К., Ричардс П. Количественная сейсмология. Т. 2. М. Мир. 1983. 880 с.
   4. Мовсесян Р. А.- Изв. вузов. Геодезия и аэрофотосъемка. 1999. №1. С. 3-17.
   5. Ризниченко Ю. В. В кн.: Исследования по физике землетрясений. М. Наука. 1976. С. 9-27.
   6. Григорян С. С. - ДАН СССР. 1989. Т. 306. №5. С. 1083-1087.
   7. Рикитаке Т. - Предсказание землетрясений. М. Мир. 1979. 388 с.
   8. Хачиян Э. Е.- ДНАН Армении. 2001. Т. 101. №1. С. 66-74.

---