2. Предположим, что примесь находится в
центре сферической КТ GaAs/Ga1-xAlxAs, ограничивающий потенциал которой
имеет вид
| U(r) = |
м
п
н
п
о |
| U1(r) = |
m1w2r2
2
|
, r <
r0 | |
|
| |
| |
(1) |
где r0 - радиус КТ, w = [1/(r0)]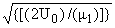 - частота ограничивающего потенциала КТ,
m1 = 0.067me - эффективная масса
электрона в полупроводнике GaAs (me - масса свободного электрона),
U0 - высота ограничивающего потенциала (для GaAs/Ga1-xAlxAs U0 = 1.247 · 0.6 · x(эВ), где x
- концентрация Al). Уравнение Шредингера для потенциала (1) будет иметь
следующий вид:
- частота ограничивающего потенциала КТ,
m1 = 0.067me - эффективная масса
электрона в полупроводнике GaAs (me - масса свободного электрона),
U0 - высота ограничивающего потенциала (для GaAs/Ga1-xAlxAs U0 = 1.247 · 0.6 · x(эВ), где x
- концентрация Al). Уравнение Шредингера для потенциала (1) будет иметь
следующий вид:
| - |
ħ 2
2m1
|
DY1 + |
m1w2r2
2
|
Y1 - |
a
r
|
Y1 = EY1, r <
r0, | |
(2) |
| - |
ħ2
2m2
|
DY2 + U0Y2 - |
a
r
|
Y2 = EY2, r і r0, | |
(3) |
где m2 = (0.067 + 0.083x)me - эффективная масса
электрона в среде из Ga1-xAlxAs,
a = [(e2)/(e)], e -
заряд электрона, Y1- волновая функция
электрона в КТ, Y2- волновая функция
электрона в окружающей среде, e є e1 = e2 - диэлектрическая проницаемость КТ и окружающей
среды (для GaAs e = 13.18). При этом мы пренебрегли
разницей между e1 и e2, так как обусловленный этой разницей эффект
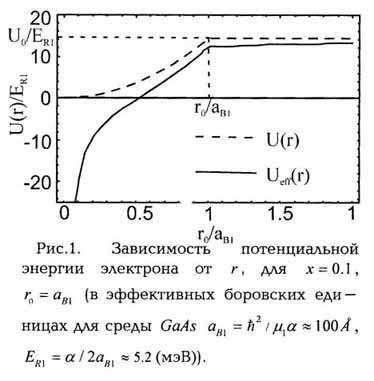
мал. Как видно из гамильтониана, электрон находится в сферической яме с
эффективной потенциальной энергией Ueff(r) = U(r) - a/r (см. рис. 1). Так как данная
задача не является точно решаемой, мы будем рассматривать ее в рамках
вариационного метода. Для этого на первой стадии обсудим задачу о поведении
электрона внутри ямы с потенциалом (1) в отсутствие примесного центра. Тогда
задача о нахождении волновых функций в двух областях r і r0 и r < r0 становится точно
решаемой, и соответствующие решения будут иметь вид
| Y(r,q,j) = |
м
п
н
п
о |
| Y1(r,q,j) = Cle-[(a1r2)/2] rl 1F1 |
й
к
л
|
nl,l + |
3
2
|
; a1r2 |
щ
ъ
ы
|
Ylm(q,j),
r <
r0 | |
|
Y2(r,q,j) = ClAlhl(+)(iklr)Ylm(q,j), r і
r0, | | |
| |
(4) |
где a1 = [(m1w)/((ħ)], nl = -[1/2]([E/(ħw)] - l - [3/2]), kl =
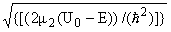 ,
Cl2 = [1/(I1l + Al2I2l)],
Al = [(e-[(a1r2)/2] rl 1F1[nl,l + [3/2];
a1r2])/(hl+(iklr))],
I1l =
,
Cl2 = [1/(I1l + Al2I2l)],
Al = [(e-[(a1r2)/2] rl 1F1[nl,l + [3/2];
a1r2])/(hl+(iklr))],
I1l =
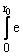 -a1r2 r2l+2{ 1F1[nl,l + [3/2];
a1r2]}2dr,
-a1r2 r2l+2{ 1F1[nl,l + [3/2];
a1r2]}2dr,
I2l =
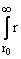 2{hl(+)(iklr)}2dr,
2{hl(+)(iklr)}2dr,
l,m - соответственно орбитальное и магнитное квантовые числа,
1F1 - вырожденная гипергеометрическая функция первого
рода, hl(+)- функция Ганкеля мнимого аргумента,
Ylm- шаровые функции. Постоянные Cl и Al
определяются из условий нормировки и непрерывности логарифмических производных
функций Y1 и Y2 в точке r = r0. Соответствующий
Enl энергетический спектр беспримесной задачи можно определить из
условия [1/(m1)][(Yў1)/(Y1)]|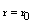 = [1/(m2)][(Yў1)/(Y2)]|
= [1/(m2)][(Yў1)/(Y2)]|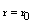 .
.
Далее, для обсуждаемой задачи пробные вариационные волновые функции
основного состояния будем рассматривать в виде
| Yv(r) = |
м
п
п
н
п
п
о
|
| Yv1(r) = |
Cv
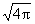 |
e-[(a1r2)/2] 1F1 |
й
к
л
|
n0, |
3
2
|
; a1r2 |
щ
ъ
ы
|
e-l[r/(aB1)],
r <
r0 | |
| Yv2(r) = |
CvAvA0
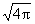 |
|
e-k0r
k0r
|
e-l[r/(aB1)],
r і
r0, | | |
| |
(5) |
где мы учли, что
h0(+)(r) = [(eir)/(r)], a
A0 = e-[(a1)/2]r02 k0r0[(1F1[n0,[3/2];a1r02])/(e-k0r0)], l - вариационный параметр, Av = exp(-l[(r0)/(aB1)](1-aB1/aB2)), aB2 = [(m1)/(m2)]aB1- эффективный боровский радиус в
среде из Ga1-xAlxAs. Постоянная
нормировки Cv выражается через вариационный параметр l посредством соотношения
| Cv2 = |
1
Iv1 + Av2A02Iv2
|
, | |
(6) |
где
| Iv1 = |
r0
у
х
0
|
e-a1r2-2l[r/(aB1)]r2 |
м
н
о |
1F1 |
й
к
л |
n0, |
3
2
|
; a1r2 |
щ
ъ
ы |
|
ь
э
ю |
2
|
dr, Iv2 = |
1
k02
|
|
Ґ
у
х
r0
|
e-2r(k0+l[1/(aB2)])dr. | |
(7) |
Определив энергию системы как
| Ev = |
у
х
0 < r
< r0
|
Yv1* |
Щ
H1
|
Yv1d |
®
r
|
+ |
у
х
r0 < r < Ґ
|
Yv2* |
Щ
H2
|
Yv2d |
®
r
|
, | |
(8) |
где
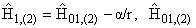 -гамильтониан беспримесной задачи в области r < r0 (r і r0), и подставляя выражения для волновых функций
(5) в (8), после преобразований для Ev получим
-гамильтониан беспримесной задачи в области r < r0 (r і r0), и подставляя выражения для волновых функций
(5) в (8), после преобразований для Ev получим
| Ev =
E0 + |
ħ2l2Cv2
2m1aB12
|
|
ж
з
и |
Iv1 +
Av2A02 |
aB1
aB2
|
Iv2 |
ц
ч
ш |
- a2Cv2(Iv3
+ Av2A02Iv4), | |
(9) | где
| Iv3 = |
r0
у
х
0
|
re-a1r2-2l[r/(aB1)] |
м
н
о |
1F1 |
й
к
л |
n0, |
3
2
|
; a1r2 |
щ
ъ
ы |
|
ь
э
ю |
2
|
dr, Iv4
= |
1
k02
|
|
Ґ
у
х
r0
|
|
1
r
|
e-2(k0+l[1/(aB2)])dr. | |
(10) |
3.
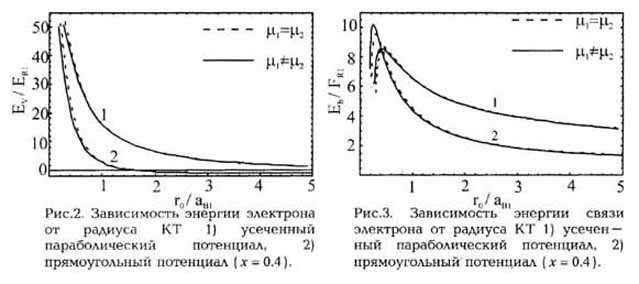
На рис. 2 представлен график зависимости энергии основного состояния примеси от
радиуса КТ, ограничивающий потенциал которой имеет вид (1) (кривая 1). Для
сравнения на том же рисунке представлена аналогичная зависимость для примеси,
находящейся в КТ с прямоугольным ограничивающим потенциалом конечной высоты
[8-10]. Из рисунка следует, что основной уровень данной задачи лежит выше
соответствующего уровня примеси в КТ с прямоугольным ограничивающим потенциалом.
С ростом r0 энергия примеси уменьшается, стремясь к значению -ER1 при r0 ® Ґ [8]. При этом разность энергий,
соответствующих случаям m1 = m2 и m1 № m2 (учет разности
эффективных масс приводит к опусканию уровня) стремится к нулю. Это обусловлено
ослаблением влияния окружающей среды на состояния примесного электрона,
локализованного в области центра КТ. Отметим, что для нашей модели эта разница
исчезает быстрее, так как при фиксированном радиусе КТ область локализации
электрона меньше, чем в случае прямоугольной ямы. Важно учесть также, что
возникновение примесных уровней носит пороговый характер, так как о них имеет
смысл говорить начиная со значений радиусов КТ, когда в ней имеется связанное
состояние при отсутствии примеси. Определив энергию связи примеси Eb
как разность между основной энергией беспримесной задачи E0 и
Ev, т.е. Eb =
E0 - Ev, можно построить зависимость Eb от
r0. На рис.3 даны графики этих зависимостей для нашего (кривая 1) и
прямоугольного (кривая 2) потенциалов. Из них следует, что с уменьшением
r0 энергия связи увеличивается, достигая максимального значения.
Eb, соответствующая нашему случаю, достигает максимального значения
при большем радиусе r0, так как из-за формы потенциала электрон
раньше "вылетает" из КТ [10]. В то же время для
|
|
прямоугольной
ямы этот радиус меньше, а максимум Eb больше, так как в этом случае
электрон прежде чем «вылететь» из ямы успевает ближе подойти к примесному
центру. Аналогичным образом интерпретируется и причина достижения максимума
Eb при больших r0 для случая m1 =
m2 по
сравнению со случаем m1 № m2.
а) Ереванский
государственный университет
б) Российско-Армянский (Славянский) государственный
университет
Литература
1. Алферов Ж. И.- ФТП. 1998. Т.32. С. 3.
2. Елисеев П. Г. - Квантовая электроника. 2000. Т. 30. P.
152.
3. Haug H. In: Spectroscopy of systems with spatially confined structures, ed. by
B. Di Bartolo [NATO Science Series, Mathematics, Physics and Chemistry. 2003.
V.90. P.61].
4. Maksym P.,
Chakraborty T.- Phys. Rev. Lett. 1990. V. 65.
P.108.
5. Peeters F. M. - Phys. Rev. 1990. B42. P. 1486
6. Kazaryan E. M., Petrosyan L. S., Sarkisyan H. A.- 23
International Colloquium on Group Theoretical Methods in Physics, Book of
Abstracts. Dubna. 2000. P.74.
7. Niculescu E.- Modern Phys. Letters. 2001. B 15. P.
545.
8. Porras-Montenegro N.,
Perez-Merchancano S. T. - J. Appl. Phys. 1993. V.74.
P.7624.
9. Zhu J. L. et al. - Phys. Rev. 1990. B 41. P. 6001.
10. Bose C., Sarkar C.- Phys. Stat. Sol.
2000. B 218. P. 461.
| ![]() - частота ограничивающего потенциала КТ,
m1 = 0.067me - эффективная масса
электрона в полупроводнике GaAs (me - масса свободного электрона),
U0 - высота ограничивающего потенциала (для GaAs/Ga1-xAlxAs U0 = 1.247 · 0.6 · x(эВ), где x
- концентрация Al). Уравнение Шредингера для потенциала (1) будет иметь
следующий вид:
- частота ограничивающего потенциала КТ,
m1 = 0.067me - эффективная масса
электрона в полупроводнике GaAs (me - масса свободного электрона),
U0 - высота ограничивающего потенциала (для GaAs/Ga1-xAlxAs U0 = 1.247 · 0.6 · x(эВ), где x
- концентрация Al). Уравнение Шредингера для потенциала (1) будет иметь
следующий вид: ![]() ,
Cl2 = [1/(I1l + Al2I2l)],
Al = [(e-[(a1r2)/2] rl 1F1[nl,l + [3/2];
a1r2])/(hl+(iklr))],
I1l =
,
Cl2 = [1/(I1l + Al2I2l)],
Al = [(e-[(a1r2)/2] rl 1F1[nl,l + [3/2];
a1r2])/(hl+(iklr))],
I1l =
![]() -a1r2 r2l+2{ 1F1[nl,l + [3/2];
a1r2]}2dr,
-a1r2 r2l+2{ 1F1[nl,l + [3/2];
a1r2]}2dr, ![]() 2{hl(+)(iklr)}2dr,
2{hl(+)(iklr)}2dr, ![]() = [1/(m2)][(Yў1)/(Y2)]|
= [1/(m2)][(Yў1)/(Y2)]|![]() .
.