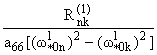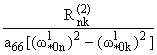ТЕОРИЯ УПРУГОСТИ
УДК 539.3
Академик Л. А. Агаловян, М. Л. Агаловян
К определению частот и форм собственных колебаний
ортотропной полосы
(Представлено 14/III 2003)
Рассматривается вопрос определения частот и
форм собственных колебаний ортотропной полосы-балки при различных, отличных от
классических, условиях на продольных краях. Установлена асимптотика компонентов
тензора напряжений и вектора перемещения, выведены характеристические уравнения
для определения значений собственных частот с заданной асимптотической
точностью. Определены собственные функции.
1. Ставится задача: найти ненулевые решения уравнений динамики теории
упругости для ортотропной полосы D = {(x,y): x О [0,l],
|y| Ј
h, h << l} при двух типах граничных условий на продольных краях y = ±h полосы:
| ux(x, ±h,
t), uy(x, ±h,
t) = 0, | |
(1.1) |
| sxy(x, h, t) = syy(x, h, t)=0,
ux(x, -h, t) = uy(x, -h, t) = 0. | |
(1.2) |
В
указанном классе задач условиям при x = 0,l соответствуют собственные колебания в
зоне пограничного слоя [1], поэтому мы их здесь не рассматриваем. Решение
сформулированной задачи ищем в виде
| sxx,sxy, syy = (s11(x,y), s12(x,y), s22(x,y))exp(iwt), | |
| |
ux,uy =
(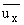 (x,y), (x,y),
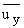 (x,y))exp(iwt). (x,y))exp(iwt). |
| |
(1.3) |
Вводя затем безразмерные переменные x =
x/l,z = y/h и компоненты вектора перемещения u =
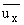 /l, v =
/l, v =
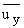 /l, решение задачи сводится к решению
сингулярно возмущенной малым параметром e = h/l системы
/l, решение задачи сводится к решению
сингулярно возмущенной малым параметром e = h/l системы
|
¶s11
¶x
|
+ e-1 |
¶s12
¶z
|
+ e-2w*2u = 0, | |
|
¶s12
¶x
|
+ e-1 |
¶s22
¶z
|
+ e-2w*2v = 0, | |
|
¶u
¶x
|
= a11s11 + a12s22, e-1 |
¶v
¶z
|
= a12s11 + a22s22, | |
(1.4) |
| e-1 |
¶u
¶z
|
+ |
¶v
¶x
|
= a66s12, w*2 = rh2w2,
| |
где w - искомая частота собственных колебаний, aik -
постоянные упругости, r -
плотность.
Решение системы (1.4) представим в
виде [2]
sy = e-1+ssy(s),
u,v = es(U(s),V(s))
s =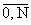 , , |
|
w*2 = ek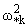 ,
k = ,
k =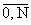 . . |
|
(1.5) |
Подставив (1.5) в (1.4), применив правило Коши умножения рядов, для
определения неизвестных коэффициентов
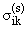 , U(s),
V(s),
, U(s),
V(s),
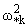 получим
рекуррентную систему
получим
рекуррентную систему
|
¶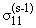
¶x
|
+ |
¶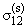
¶z
|
+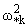 U(s-k) = 0, k = U(s-k) = 0, k =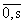 , , |
|
|
¶U(s-1)
¶x
|
= a11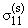 + a12 + a12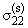 , , | |
(1.6) |
|
¶V(s)
¶z
|
= a12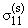 + a22 + a22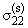 , , | |
|
¶U(s)
¶z
|
+ |
¶V(s-1)
¶x
|
= a66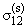 ,
Q(m) є
0, m < 0, ,
Q(m) є
0, m < 0, | |
где
k =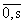 всегда означает, что по немому
(повторяющемуся) индексу "k" происходит суммирование в пределах 0,s. Из системы
(1.6) следуют
всегда означает, что по немому
(повторяющемуся) индексу "k" происходит суммирование в пределах 0,s. Из системы
(1.6) следуют
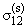 = = |
1
a66
|
|
й
к
л |
|
¶U(s)
¶z
|
+ |
¶V(s-1)
¶x
|
|
щ
ъ
ы |
, 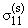 = = |
1
D
|
|
й
к
л |
- a12 |
¶V(s)
¶z
|
+ a22 |
¶U(s-1)
¶x
|
|
щ
ъ
ы |
, | |
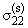 = = |
1
D
|
|
й
к
л |
a11 |
¶V(s)
¶z
|
- a12 |
¶U(s-1)
¶x
|
|
щ
ъ
ы |
, D = a11a22 -
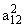 , , | |
(1.7) |
функции U(s),
V(s) определяются из уравнений
|
|
¶2U(s)
¶z2
|
+ a 66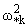 U(s-k) = fu(s),
k = U(s-k) = fu(s),
k =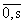 , , |
|
| fu(s) = -a66 |
¶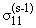
¶x
|
- |
¶2V(s-1)
¶x¶z
|
, | | |
| |
(1.8) |
|
|
¶2V(s)
¶z2
|
+ A11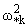 V(s-k) = fv(s), V(s-k) = fv(s),
| |
| fv(s) = -A11 |
¶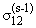
¶x
|
+ |
a12
a11
|
|
¶2U(s-1)
¶x¶z
|
,
A11 = D/a11. | | |
| |
(1.9) |
При s = 0 уравнения (1.8), (1,9) однородны и независимы. Решив их,
определив по формулам (1.7) остальные искомые величины и удовлетворив условиям
(1.1) или (1.2), получим характеристические уравнения для определения главных
значений частот собственных колебаний. Затем определяются соответствующие им
собственные функции. Условиям ux(±h) = 0
соответствуют следующие характеристические уравнения и главные значения частот:
|
| |
а) cos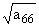 w*0 = 0, w*0 = 0, 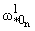 = =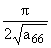 (2n+1), n О N (2n+1), n О N |
| |
|
| |
| |
(1.10) |
|
| |
б) sin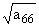 w*0 = 0, w*0 = 0, 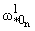 = =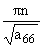 , n О N (задача
изгиба), , n О N (задача
изгиба), |
| | |
| |
(1.11) |
Собственными функциями являются
соответственно
| ynI(z) = cos |
p
2
|
(2n+1)z, jnI(z) = sinpnz. | |
(1.12) |
Легко убедиться, что они
составляют ортонормированную систему
|
+1
у
х
-1
|
ynI(z)ymI(z)¶z = dmn,
|
+1
у
х
-1
|
jnI(z)jmI(z)¶z = dmn. | |
(1.13) |
Имеем
а)
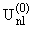 = =
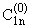 (x)ynI(z), б) (x)ynI(z), б) 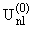 = =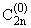 (x)ynI(z). (x)ynI(z). | |
(1.14) |
Частотам (1.10), (1.11)
соответствуют сдвиговые собственные колебания. Условиям uy(±h) = 0 соответствуют
|
| |
а) sinw*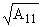 = 0, = 0, 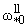 = =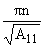 , n
О N, (симетричная
задача) , n
О N, (симетричная
задача) |
| | |
| |
(1.15) |
|
| |
б) cosw*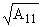 = 0, = 0, 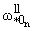 = =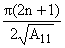 , n О N (задача
изгиба), , n О N (задача
изгиба), |
| |
| |
(1.16) |
Собственными функциями являются
функции (1.12). Имеем
а)
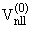 = =
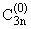 (x)ynI(z), б) (x)ynI(z), б)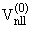 = =
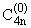 (x)ynI(z). (x)ynI(z). | |
(1.17) |
Собственные колебания являются
продольными.
Граничным условиям (1.2)
соответствуют следующие главные значения частот сдвиговых и продольных колебаний
и соответствующие им собственные функции, которые также составляют
ортонормированную систему:
| ynI, II = sin |
p
4
|
(2n+1)(1+z). | |
(1.19) |
2. При s > 0 необходимо найти решения уравнений (1.8), (1.9) для двух
независимых случаев: а)w*k =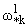 , б) w*k =
, б) w*k =
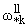 , которым будут соответствовать
решения
, которым будут соответствовать
решения
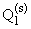 ,
,
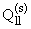 . В частности,
. В частности,
При s = 1 и w*0 =
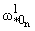 уравнение (1.8)
принимает вид
уравнение (1.8)
принимает вид
|
|
¶2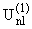
¶z2
|
+ a66(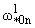 )2 )2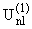 + a66 + a66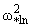 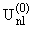 = =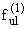 , ,
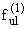 = -a66 = -a66 |
¶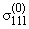
¶x
|
- |
¶2VI(0)
¶x¶z
|
. | | |
| |
(2.2) |
В
уравнении (2.2) неизвестными являются функция
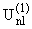 и
поправка к частоте
и
поправка к частоте
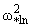 . Для их
определения применим следующий прием решения подобных уравнений [3,4]. Решение
будем искать в виде ряда по системе функций {ynI}:
. Для их
определения применим следующий прием решения подобных уравнений [3,4]. Решение
будем искать в виде ряда по системе функций {ynI}:
При таком представлении решения граничные условия (1.1) удовлетворяются
тождественно. Представив
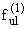 в виде ряда по функциям
{ynI}, затем умножив обе части
уравнения (2.2) на ykI(z) и используя свойство (1.13), получим
в виде ряда по функциям
{ynI}, затем умножив обе части
уравнения (2.2) на ykI(z) и используя свойство (1.13), получим
|
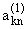 =
= 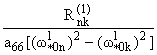 (k № n),
(k № n), |
|
|
| |
| |
(2.4) |
ann определяется из
условия нормировки [3,4]:
|
+1
у
х
-1
|
(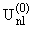 + e + e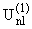 )2dz = 1. )2dz = 1. | |
(2.5) |
Согласно (1.8), (2.1)
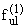 = 0, следовательно
= 0, следовательно
При s=2 повторяется та же процедура. В результате имеем
|
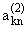 = =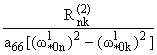 (k № n),
(k № n),
|
|
|
| |
| |
(2.7) |
где
|
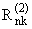 = = |
+1
у
х
-1
|
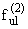 yk(z)dz, yk(z)dz, | |
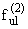 = -a66 = -a66 |
¶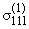
¶x
|
- |
¶2VI(1)
¶x¶z
|
, | | |
| |
(2.8) |
а VI(1)
однозначно определяется из неоднородного уравнения (1.9) при w*0 = w*0I и
граничных условий (1.1),
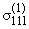 вычисляется по формуле (1.7). Эту процедуру можно продолжить и при s > 2,
однако в практических приложениях бывает достаточным ограничиться приближениями
s = 0,1,2. В нашем случае имеем
вычисляется по формуле (1.7). Эту процедуру можно продолжить и при s > 2,
однако в практических приложениях бывает достаточным ограничиться приближениями
s = 0,1,2. В нашем случае имеем
т.е. сдвиговые собственные
колебания будут возбуждать продольные колебания с той же частотой, но малой
амплитудой и наоборот. Данные для задачи изгиба можно получить из
вышеприведенных формальной заменой функций yk(z) на jk(z). Изложенную
процедуру можно повторить для случая w*n =
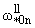 . Здесь главенствующую роль будет
играть уравнение (1.9). Поправка к частоте будет порядка O(e2), продольные же колебания будут возбуждать
собственные сдвиговые колебания малой амплитуды.
. Здесь главенствующую роль будет
играть уравнение (1.9). Поправка к частоте будет порядка O(e2), продольные же колебания будут возбуждать
собственные сдвиговые колебания малой амплитуды.
Подобным образом осуществляется процесс определения решения при
граничных условиях (1.2).
Институт механики НАН PА
Литература
1. Агаловян М. Л. В кн.: Современные вопросы оптимального управления и устойчивости
систем. Ереван. Изд.-во ЕГУ. 1997. С. 132-135.
2. Агаловян Л. А.- Асимптотическая теория
анизотропных пластин и оболочек. М. Наука. 1997. 414
с.
3. Найфе А. Х.- Методы возмущений. М. Мир. 1976. 455 с.
4. Ломов С. А.- Введение в общую теорию
сингулярных возмущений. М. Наука. 1981. 398 с.
![]() /l, v =
/l, v =
![]() /l, решение задачи сводится к решению
сингулярно возмущенной малым параметром e = h/l системы
/l, решение задачи сводится к решению
сингулярно возмущенной малым параметром e = h/l системы
![]() , U(s),
V(s),
, U(s),
V(s),
![]() получим
рекуррентную систему
получим
рекуррентную систему ![]() всегда означает, что по немому
(повторяющемуся) индексу "k" происходит суммирование в пределах 0,s. Из системы
(1.6) следуют
всегда означает, что по немому
(повторяющемуся) индексу "k" происходит суммирование в пределах 0,s. Из системы
(1.6) следуют ![]() , б) w*k =
, б) w*k =
![]() , которым будут соответствовать
решения
, которым будут соответствовать
решения
![]() ,
,
![]() . В частности,
. В частности,
![]() и
поправка к частоте
и
поправка к частоте
![]() . Для их
определения применим следующий прием решения подобных уравнений [3,4]. Решение
будем искать в виде ряда по системе функций {ynI}:
. Для их
определения применим следующий прием решения подобных уравнений [3,4]. Решение
будем искать в виде ряда по системе функций {ynI}: ![]() в виде ряда по функциям
{ynI}, затем умножив обе части
уравнения (2.2) на ykI(z) и используя свойство (1.13), получим
в виде ряда по функциям
{ynI}, затем умножив обе части
уравнения (2.2) на ykI(z) и используя свойство (1.13), получим ![]() вычисляется по формуле (1.7). Эту процедуру можно продолжить и при s > 2,
однако в практических приложениях бывает достаточным ограничиться приближениями
s = 0,1,2. В нашем случае имеем
вычисляется по формуле (1.7). Эту процедуру можно продолжить и при s > 2,
однако в практических приложениях бывает достаточным ограничиться приближениями
s = 0,1,2. В нашем случае имеем ![]() . Здесь главенствующую роль будет
играть уравнение (1.9). Поправка к частоте будет порядка O(e2), продольные же колебания будут возбуждать
собственные сдвиговые колебания малой амплитуды.
. Здесь главенствующую роль будет
играть уравнение (1.9). Поправка к частоте будет порядка O(e2), продольные же колебания будут возбуждать
собственные сдвиговые колебания малой амплитуды.