МЕХАНИКА
УДК 531.8
Р. М. Киракосян, М. С. Саркисян
Свободные продольные колебания ортотропных полос
линейно-переменной толщины при учете обжатия
(Представлено
академиком С. А. Амбарцумяном 4/VII 2003)
1. Рассмотрим ортотропную пластинку-полосу.
Координатную плоскость xOy совместим со срединной плоскостью, направив ось x
вдоль ширины, а ось y-вдоль одной из кромок полосы. Главные направления
анизотропии материала параллельны координатным осям. Толщина полосы изменяется
вдоль ширины по закону
| h = h0 |
ж
з
и |
1 -d |
x
l
|
|
ц
ч
ш |
, h0 > 0,
d <
1. | |
(1.1) |
Здесь l-ширина полосы, h0 и d -
заданные постоянные. Полоса закреплена вдоль кромки x = 0 и растянута равномерно
распределенными силами погонной интенсивности P , приложенными на кромке x = l.
Рассмотрим задачу о свободных продольных колебаниях полосы, возникающих после ее
внезапного освобождения от сил. Будем пользоваться уравнениями и соотношениями
[1], учитывающими влияние обжатия. Родственная задача для стержней переменого
поперечного сечения в классической постановке рассмотрена в [2].
Второе уравнение плоской задачи полосы [1]
удовлетворяется автоматически, а первое с учетом сил инерции можно представить в
виде
| d2 |
ж
з
и |
|
¶2u
¶H2
|
+ |
1
H
|
|
¶u
¶H
|
|
ц
ч
ш |
= |
l2
a2
|
|
¶2u
¶t2
|
. | |
(1.2) |
Здесь u-перемещение вдоль оси x, t-время,
r-плотность материала полосы,
| H = 1 - d |
x
l
|
, a2 = |
4B11
r(4+A1d2s2)
|
, s = |
h0
l
|
. | |
(1.3) |
Величины B11 и A1 выражаются через соответствующие
модули Юнга Ei и коэффициенты Пуассона материала nij по известным формулам [4]:
| B11 = |
E1
1 - n12n21
|
, A1 = - |
E1
E3
|
|
n13 + n12n23
1 - n12n21
|
. | |
(1.4) |
Отметим, что влияние обжатия в данной задаче учитывается параметром
A1. Положив в (1.2)
приходим к следующим двум
обыкновенным дифференциальным уравнениям:
|
¶2X
¶H2
|
+ |
1
H
|
|
¶X
¶H
|
+ |
w2
d2
|
X = 0, |
¶2T
¶t2
|
+ |
a2
l2
|
w2
T = 0, | |
(1.6) |
где w -
произвольная вещественная постоянная. Общие решения уравнений (1.6) имеют вид
| X = C1J0 |
ж
з
и |
|
w
d
|
H |
ц
ч
ш |
+ C2Y0 |
ж
з
и |
|
w
d
|
H |
ц
ч
ш |
, | |
(1.7) |
| T = C3cos |
wa
l
|
t + C4sin |
wa
l
|
t. | |
(1.8) |
Здесь J0 и Y0 - бесселевые функции нулевого
индекса первого и второго родов соответственно. Ci - неизвестные
постоянные, подлежащие определению из граничных и начальных условий задачи:
1) при H = 1, u = 0; 3) при
t = 0, [(¶u)/(¶t)] = 0
2) при H = 1 - d,
[(¶u)/(¶H)] = 0; 4) при t = 0,
u = -[(P(4 + A1d2s2))/(4B11ds)]ln H.
(1.9)
Из первых двух условий (1.9) следует
| C1J0 |
ж
з
и |
|
w
d
|
|
ц
ч
ш |
+ C2Y0 |
ж
з
и |
|
w
d
|
|
ц
ч
ш |
= 0, | |
| C1J1 |
ж
з
и |
|
w
l
|
|
ц
ч
ш |
+ C2Y1 |
ж
з
и |
|
w
l
|
|
ц
ч
ш |
= 0, l = |
d
1-d
|
, | |
(1.10) |
а из третьего условия -
C4 = 0. Из (1.10) для определения w получается
трансцендентное уравнение, которое имеет бесконечное множество корней wn (n = 1,2,3,...)
| J0 |
ж
з
и |
|
wn
d
|
|
ц
ч
ш |
Y1 |
ж
з
и |
|
wn
l
|
|
ц
ч
ш |
- Y0 |
ж
з
и |
|
wn
d
|
|
ц
ч
ш |
J1 |
ж
з
и |
|
wn
l
|
|
ц
ч
ш |
= 0. | |
(1.11) |
В
случае полосы постоянной толщины d = 0 уравнение (1.11)
сводится к уравнению
корнями которого являются числа
| wn = (2n - 1) |
p
2
|
,
n = 1,2,3,... | |
(1.13) |
Выразив C2 через
C1, можно общее решение задачи представить в виде
| u(x,t) = |
Ґ
е
n=1
|
Bn |
й
к
л |
Y0 |
ж
з
и |
|
wn
d
|
|
ц
ч
ш |
J0 |
ж
з
и |
|
wn
d
|
H |
ц
ч
ш |
- J0 |
ж
з
и |
|
wn
d
|
|
ц
ч
ш |
Y0 |
ж
з
и |
|
wn
d
|
H |
ц
ч
ш |
|
щ
ъ
ы |
cos |
wn a
l
|
t. | |
(1.14) |
Следуя [2] и используя четвертое условие
(1.9), можно определить коэффициенты Bn, после чего формула
перемещения примет следующий вид:
| u(x,t) = |
pP
s(1-d)
|
· |
4 + A1d2s2
4B11
|
|
Ґ
е
n=1
|
|
| J0 |
ж
з
и
|
|
wn
d
|
|
ц
ч
ш
|
J1 |
ж
з
и
|
|
wn
l
|
|
ц
ч
ш
|
| wn |
й
к
л
|
J02 |
ж
з
и
|
|
wn
d
|
|
ц
ч
ш
|
- J12 |
ж
з
и
|
|
wn
l
|
|
ц
ч
ш
|
|
щ
ъ
ы
|
| |
× | |
(1.15) |
| × |
й
к
л |
Y0 |
ж
з
и |
|
wn
d
|
|
ц
ч
ш |
J0 |
ж
з
и |
|
wn
d
|
H |
ц
ч
ш |
- J0 |
ж
з
и |
|
wn
d
|
|
ц
ч
ш |
Y0 |
ж
з
и |
|
wn
d
|
H |
ц
ч
ш |
|
щ
ъ
ы |
cos |
wn a
l
|
t. | |
В случае полосы постоянной толщины приходим к
формуле, аналогичной формуле перемещения стержня постоянного поперечного сечения
[2,3]
| u(x,t) = |
8P
B11sp2
|
|
Ґ
е
n=1
|
|
(-1)n-1
(2n-1)2
|
sin |
2n-1
2l
|
pxcos |
2n-1
2l
|
pat,
a = |
B11
r
|
. | |
(1.16) |
2. Корни трансцендентных уравнений (1.11) и (1.12) не зависят ни от
ширины полосы, ни от механических свойств ее материала. Они определяются
заданием лишь параметра
что зависит только от отношения
толщин краев полосы. В таблице представлены первые четыре корня wn для некоторых значений d.
| n |
d |
-10 |
-1 |
-0.4 |
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
| 1 |
0.709 |
1.361 |
1.466 |
1.571 |
1.642 |
1.735 |
1.864 |
2.059 |
2.405 |
| 2 |
4.246 |
4.646 |
4.679 |
4.712 |
4.737 |
4.775 |
4.839 |
4.986 |
5.519 |
| 3 |
7.470 |
7.814 |
7.834 |
7.854 |
7.869 |
7.892 |
7.933 |
8.038 |
8.653 |
| 4 |
10.658 |
10.967 |
10.981 |
10.996 |
11.006 |
11.023 |
11.053 |
11.133 |
11.790 |
Круговые частоты свободных продольных
колебаний полосы определяются формулой
Wn=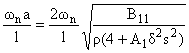 |
. | |
(2.2) |
Соответствующие классические значения
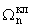 , которые
получаются без учета обжатия, будут
, которые
получаются без учета обжатия, будут
Следовательно,
Wn =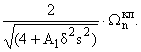
|
|
(2.4) |
Из (2.4) заключаем:
1. В случае постоянной толщины (d = 0) учет обжатия не
влияет на значения собственных частот продольных колебаний полосы Wn.
2. Так как A1 < 0, то учет обжатия при переменности толщины приводит
к увеличению собственных частот, т.е. Wn >
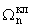 . Причем это не зависит от знака
d, т.е. от того, как изменяется толщина полосы с удалением от ее
закрепленного края - убывает она или возрастает.
. Причем это не зависит от знака
d, т.е. от того, как изменяется толщина полосы с удалением от ее
закрепленного края - убывает она или возрастает.
3. Увеличение Wn не зависит от номера n, т.е.
оно одинаково для всех собственных частот.
4. Влияние обжатия на значение Wn обычно
мало. Например, в случае изотропной полосы при v = 1/3 и dh/dx = 1/4 имеем
A1 = -0.5, d2s2 = 1/16,
Wn = 1.004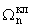 , , | |
(2.5) |
В
данном случае учет обжатия увеличивает значения всех частот лишь на 0.4%. Однако
в настоящее время существуют такие композиционные ортотропные материалы, модуль
Юнга которых в поперечном направлении на один, два порядка меньше, чем в
направлении армирования. При таких материалах влияние обжатия на значения Wn может оказаться существенным. Например, при
A1 = -10, что для отмеченных материалов вполне
реально, в случае dh/dx = 1/4 имеем
Wn = 1.089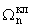 , , | |
(2.6) |
т.е. учет обжатия примерно на 9%
увеличивает собственные частоты. Разумеется, при материалах с более сильной
анизотропией эта цифра будет еще большей.
5. Данные таблицы с учетом (2.3) показывают,
что в случае отрицательных d, т.е. когда с удалением от
закрепленного края полоса утолщается, классические частоты
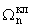 становятся
меньше частот соответствующей полосы постоянной толщины. Причем чем сильнее
утолщается полоса (чем больше абсолютное значение d),
тем сильнее уменьшаются частоты. Этот факт физически можно объяснить тем, что
утолщение полосы как бы играет роль добавления к полосе постоянной толщины
присоединенных масс. Аналогично можно объснить и обратное явление - увеличение
классических частот при положительных d. В этом случае
с удалением от закрепленного края полоса утоньшается, что равносильно отбавлению
масс от соответствующей полосы постоянной толщины.
становятся
меньше частот соответствующей полосы постоянной толщины. Причем чем сильнее
утолщается полоса (чем больше абсолютное значение d),
тем сильнее уменьшаются частоты. Этот факт физически можно объяснить тем, что
утолщение полосы как бы играет роль добавления к полосе постоянной толщины
присоединенных масс. Аналогично можно объснить и обратное явление - увеличение
классических частот при положительных d. В этом случае
с удалением от закрепленного края полоса утоньшается, что равносильно отбавлению
масс от соответствующей полосы постоянной толщины.
6. Так как A1 < 0, то с ростом
|dh/dx| = |d|s
знаменатель (2.4) уменьшается. При положительных d это
приведет к усилению возрастания неклассических частот, поскольку в этом случае
убывание знаменателя дроби (2.4) сопровождается ростом ее числителя. В случаях
же отрицательных d с ростом |d|s
одновременно убывают и знаменатель и числитель (2.4). Это приведет к ослаблению
уменьшения неклассических частот. Возможны случаи, когда учет обжатия при d < 0 приведет к тому, что частоты сравняются и даже
станут большe соответствующих частот полосы постоянной толщины. Например, при
d = -1, s = 1/8,
A1 = -64 имеет место равенство
| W1|d = -1 = 1.571 = W1|d = 0. | |
(2.7) |
В
случае же d = -1, s = 1/8,
A1 = -80 первая частота становится больше
первой частоты полосы постоянной толщины:
| W1|d = -1 = 1.641 > W1|d = 0 = 1.571. | |
(2.8) |
Материалы с такими значениями параметра A1 очень сильно
анизотропны. Модуль Юнга таких материалов в поперечном направлении примерно на
два порядка меньше, чем в направлении армирования.
Институт механики НАН РА
Литература
1. Киракосян Р. М. - Изв. НАН Армении. Механика. 2002. Т. 55, 4. С.12-23
2.
Гаспарян А. Е., Хачатрян А. А. - Изв. НАН
Армении. Механика. 1994. Т. 47. N 5-6. С.14-23
3. Тимошенко С. П. Колебания в инженерном деле. М. Физматгиз.
1959. 440 с.
4. Амбарцумян С. А. Теория анизотропных пластин. М. Наука. 1987. 360 с.
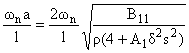
![]() , которые
получаются без учета обжатия, будут
, которые
получаются без учета обжатия, будут ![]()
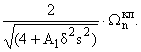
![]() . Причем это не зависит от знака
d, т.е. от того, как изменяется толщина полосы с удалением от ее
закрепленного края - убывает она или возрастает.
. Причем это не зависит от знака
d, т.е. от того, как изменяется толщина полосы с удалением от ее
закрепленного края - убывает она или возрастает.![]() ,
,![]() ,
,![]() становятся
меньше частот соответствующей полосы постоянной толщины. Причем чем сильнее
утолщается полоса (чем больше абсолютное значение d),
тем сильнее уменьшаются частоты. Этот факт физически можно объяснить тем, что
утолщение полосы как бы играет роль добавления к полосе постоянной толщины
присоединенных масс. Аналогично можно объснить и обратное явление - увеличение
классических частот при положительных d. В этом случае
с удалением от закрепленного края полоса утоньшается, что равносильно отбавлению
масс от соответствующей полосы постоянной толщины.
становятся
меньше частот соответствующей полосы постоянной толщины. Причем чем сильнее
утолщается полоса (чем больше абсолютное значение d),
тем сильнее уменьшаются частоты. Этот факт физически можно объяснить тем, что
утолщение полосы как бы играет роль добавления к полосе постоянной толщины
присоединенных масс. Аналогично можно объснить и обратное явление - увеличение
классических частот при положительных d. В этом случае
с удалением от закрепленного края полоса утоньшается, что равносильно отбавлению
масс от соответствующей полосы постоянной толщины.