МАТЕМАТИКА
УДК 519.21
Э. А. Даниелян, Э. А. Симонян
Обобщение закона сохранения Клейнрока
(Представлено академиком А. А. Терзяном 8/V 2003)
В классе консервативных дисциплин модели
Mr |Gr|1|Ґ
действуют универсальные законы сохранения. К их числу относится закон сохранения
работы Л. Клейнрока, связывающий средние стационарные времена ожидания вызовов
различных потоков (см. [1], с. 138), при недопущении прерываний обслуживания. В
настоящей работе данный закон сохранения обобщен на случай допущения прерываний
обслуживания и применен к дисциплине абсолютных приоритетов.
В одноканальную систему обслуживания с
ожиданием поступают независимые пуассоновские потоки 1-вызовов, ..., r-вызовов с
параметрами a1 > 0, ..., ar > 0 соответственно.
Длительности обслуживания вызовов независимы, не зависят от процесса поступления
и для k-вызовов, k =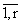 , имеют функцию распределения
(ФР) Bk(x), Bk(+0) = 0.
, имеют функцию распределения
(ФР) Bk(x), Bk(+0) = 0.
В рамках описанной модели Mr
|Gr|1|Ґ рассмотрим класс консервативных
дисциплин, для которых внутри потоков действует дисциплина FIFO (first in -
first out). Дисциплина обслуживания консервативна, если
внутри модели работа (время обслуживания) не возникает и не исчезает, а лишь
привносится в модель поступлением вызовов. Обозначим
| R = r1 + r2 + ... +rr,
W0 = |
1
2
|
|
r
е
k=1
|
akbk2, | |
где
rk = akbk1, bki =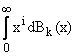 ,
k = ,
k =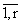 , i
= 1,2. , i
= 1,2. |
|
Если консервативная дисциплина обслуживания задается на первом периоде
занятости модели Mr |Gr|1|Ґ и в точности повторяется на
последующих периодах занятости, то в работах [2,3] развит метод доказательства
существования при R < 1 вводимых ниже стационарных характеристик. В настоящей
работе рассмотрен именно такой подкласс консервативных дисциплин.
Нас интересуют следующие средние стационарные
характеристики:
Wk, k =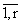 , - среднее стационарное время ожидания k-вызова до
момента первого его поступления на прибор;
, - среднее стационарное время ожидания k-вызова до
момента первого его поступления на прибор;
Vk, k =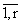 , - среднее стационарное время ожидания k-вызова в очереди до момента ухода его из модели обслуженным;
, - среднее стационарное время ожидания k-вызова в очереди до момента ухода его из модели обслуженным;
Uk, k =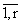 , - среднее стационарное время пребывания k-вызова в
модели, т.е. время с момента поступления k-вызова в модель до момента ухода его
из модели обслуженным;
, - среднее стационарное время пребывания k-вызова в
модели, т.е. время с момента поступления k-вызова в модель до момента ухода его
из модели обслуженным;
Hk, k =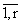 , - среднее (условно) стационарное время пребывания
k-вызова на приборе, т.е. среднее время, начинающееся с момента первого
поступления k-вызова на прибор и завершающееся моментом ухода его из модели.
, - среднее (условно) стационарное время пребывания
k-вызова на приборе, т.е. среднее время, начинающееся с момента первого
поступления k-вызова на прибор и завершающееся моментом ухода его из модели.
При недопущении прерываний обслуживания
Wk = Vk, Hk = bk1, а в общем случае
Uk = Wk + Hk = Vk + bk1, k =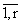 |
|
(1) |
При
недопущении прерываний обслуживания закон сохранения работы Л. Клейнрока в
предположении R < 1 записывается в виде
|
r
е
k=1
|
rk · Wk = |
RW0
1 - R
|
. | |
(2) |
Закон сохранения (2) позволяет сделать следующее обобщение.
Теорема. При R < 1 в рассматриваемом
подклассе консервативных дисциплин (с прерываниями или без прерываний
обслуживания) модели Mr |Gr|1|Ґ имеет место следующий закон
сохранения:
|
r
е
k=1
|
rk · Wkm+ |
r
е
k=1
|
ak · |
bk2
2bk1
|
Hk = |
W0
1-R
|
. | |
(3) |
Если
прерывания обслуживания не допускаются, то (2) следует из (3). Действительно, в
данном случае Hk = bk1, k =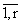 , и
, и
|
r
е
k=1
|
ak · |
bk2
2bk1
|
Hk = W0, | |
откуда
и из (3) следует (2).
Примером консервативной дисциплины с
прерываниями обслуживания, для которой справедлива формула (3), является
дисциплина абсолютных с дообслуживанием приоритетов (см.,
например, [2]). Именно, i-вызов, поступая в модель, замещает j-вызов на приборе
при i < j. Прерванный j-вызов возвращается в очередь и при новом попадании на
прибор дообслуживается. В очереди i-вызовы становятся впереди j-вызовов при i
< j.
Из (3) вытекает следующий известный
результат: при R < 1 и дисциплине абсолютных с дообслуживанием приоритетов в
модели Mr |Gr|1|Ґ
| Wk = |
W0k
(1 - Rk-1)(1 - Rk)
|
, k =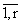 |
|
(4) |
где
| Rk = r1 + r2 + ... + rr,
W0k = |
1
2
|
|
k
е
i=1
|
aibi2, k =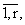 |
R0 = 0. | |
Действительно, отметим, что стационарное время пребывания k-вызова на
приборе hk представимо в виде
|
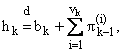
|
(5) |
где символ d указывает на совпадение
ФР обеих частей равенства. Здесь: bk - случайное время обслуживания
k-вызова;
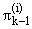 одинаково распределены с периодом
занятости обслуживанием
одинаково распределены с периодом
занятости обслуживанием
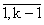 -вызовов (1- вызовов, ..., (k-1)-вызовов); vk - случайное число
-вызовов (1- вызовов, ..., (k-1)-вызовов); vk - случайное число
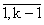 -вызовов, поступающих в
модель за bk, не зависящее от {
-вызовов, поступающих в
модель за bk, не зависящее от {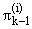 }.
}.
Переходя в (5) к математическим ожиданиям, по
формуле Вальда получаем
| Hk = bk1 · {1 + sk-1 · Pk-1}, | |
(6) |
где sk-1 = a1+...+ak-1, Pk-1 - среднее периода занятости обслуживанием
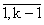 -вызовов. Pk-1 совпадает со средним
периода занятости модели M |G|1|Ґ с
параметром sk-1
поступления и с ФР
-вызовов. Pk-1 совпадает со средним
периода занятости модели M |G|1|Ґ с
параметром sk-1
поступления и с ФР
|
k-1
е
i=1
|
(ai/sk-1)Bi(x), x і
0, | |
времени обслуживания
вызовов. Поэтому sk-1Pk-1 = Rk-1/(1-Rk-1). Подставляя эти
равенства в (6), находим
| Hk = |
bk1
1 - Rk-1
|
, k =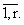 |
|
(7) |
Поскольку при каждом k =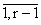 потоки (k + 1)-вызовов, ..., r-вызовов не влияют на
величины Wi и Hi, i =
потоки (k + 1)-вызовов, ..., r-вызовов не влияют на
величины Wi и Hi, i =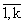 , то
для абсолютных с дообслуживанием приоритетов из (3) и (7) следует система
уравнений
, то
для абсолютных с дообслуживанием приоритетов из (3) и (7) следует система
уравнений
|
k
е
i=1
|
riWi + |
k
е
i=1
|
|
aibi2
2 · (1 - Ri-1)
|
= |
W0(k)
1 - Rk
|
, k =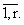 |
|
(8) |
Вычитая из k-того уравнения (8) (k-1)-ое,
находим
| rkWk = W0(k) · |
м
н
о |
|
1
1 - Rk
|
- |
1
1 - Rk-1
|
|
ь
э
ю |
= rk · |
W0(k)
(1 - Rk-1)(1 - Rk)
|
, k =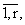 |
|
что
равносильно (4).
Набросок доказательства теоремы дан в
приложении.
Приложение. В любой
момент времени в модели есть не более одного прерванного вызова каждого потока.
Обозначим: Nk(t) - число еще не
тронутых обслуживанием k-вызовов в модели в момент t; Tk(t) - число
k-вызовов в модели в момент t, успевших побывать на приборе; Lk(t)
равно единице, если в момент t обслуживается k-вызов, и равно нулю в противном
случае.
Введенные процессы являются регенерирующими.
К ним применима теорема из [3], с. 430. Как и в [4], при R < 1 и t ® +Ґ для них существуют стационарные
аналоги Nk, Tk и Lk. При этом
P(Lk = 1) = P(Tk = 1) = rk > 0, k =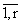 |
| |
(9) |
где P- знак вероятности.
Пусть: xik - длительность
обслуживания i-того k-вызова из числа Nk(t); yk(t) -
условное остаточное время обслуживания тронутого в момент t обслуживанием
k-вызова при условии Tk(t) = 1.
Из временной оси выкинем промежутки, за
которые не было тронутых обслуживанием k-вызовов, и уплотним временную ось. На
временной оси каждому моменту t соответствует на уплотненной временной оси
момент u = zk(t). Из уплотненной временной оси
выкинем промежутки, за которые на приборе находится k-вызов, и образуем дважды
уплотненную временную ось. Каждому моменту u на уплотненной оси соответствует
момент v = xk(u) на дважды уплотненной.
В силу (9), по усиленному закону больших
чисел,
|
lim
t®+Ґ
|
zk(t) = +Ґ,
|
lim
t®+Ґ
|
xk(zk(t)) = +Ґ почти всюду. | |
(10) |
Величина yk(t) интерпретируется
как остаточное время восстановления в момент xk(zk(t)) на
дважды уплотненной временной оси для процесса восстановления {xk(i)}, где xk(i), i і 1,
независимы и имеют ФР Bk(t). Поэтому существует стационарный при
t ® +Ґ аналог yk
величины yk(t) (см. (10)), причем
Myk = (bk2/2bk1), k =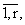 |
|
(11) |
где M - знак математического
ожидания. Справедливо равенство
| w(t) = |
r
е
k=1
|
|
ж
з
и |
|
Nk(t)
е
i=1
|
xik + |
м
н
о |
|
|
ц
ч
ш |
, t і 0, | |
где
w(t) - накопленная и не выполненная к моменту t работа.
Отсюда по формуле Вальда (Nk(t) не
зависит от будущего),
| Mw(t) = |
r
е
k=1
|
(bk1 · MNk(t) + P{Tk(t) = 1} · Myk(t)). | |
(12) |
Поскольку существуют предел [(W0)/(1-R)] =
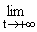 Mw(t) (см.,
например, [2]) и стационарные Nk, Tk и Myk,
k = Mw(t) (см.,
например, [2]) и стационарные Nk, Tk и Myk,
k =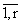 , то, переходя к пределу t ® +Ґ в (12), с учетом
P{Tk = 1} = MTk и (11), получаем , то, переходя к пределу t ® +Ґ в (12), с учетом
P{Tk = 1} = MTk и (11), получаем
|
W0
1 - R
|
= |
r
е
k=1
|
bk1 · MNk + |
r
е
k=1
|
|
bk2
2bk1
|
MTk. | |
(13) | По
формулам Литтля для средних характеристик, используя (1), имеем
MNk = akWk, M(Nk + Tk) = akUk = akWk + akHk,
k =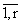 . . |
| Подставляя последние равенства в (13), выводим (3).
Ереванский государственный университет
Литература
1. Клейнрок Л. Вычислительные системы с очередями. М. Мир. 1979. 600
с.
2. Климов Г. П. Стохастические системы обслуживания. М. Наука. 1966.
3. Феллер В. Введение в теорию вероятностей и ее приложения. Т. 2. М. Мир. 1984. 751
с.
4. Даниелян Э. А., Хачикян
Т. З.- Уч. зап. ЕГУ. 2001. N1. С. 4-22.
|
![]() , - среднее стационарное время ожидания k-вызова до
момента первого его поступления на прибор;
, - среднее стационарное время ожидания k-вызова до
момента первого его поступления на прибор; ![]() , - среднее стационарное время ожидания k-вызова в очереди до момента ухода его из модели обслуженным;
, - среднее стационарное время ожидания k-вызова в очереди до момента ухода его из модели обслуженным;![]() , - среднее стационарное время пребывания k-вызова в
модели, т.е. время с момента поступления k-вызова в модель до момента ухода его
из модели обслуженным;
, - среднее стационарное время пребывания k-вызова в
модели, т.е. время с момента поступления k-вызова в модель до момента ухода его
из модели обслуженным;![]() , - среднее (условно) стационарное время пребывания
k-вызова на приборе, т.е. среднее время, начинающееся с момента первого
поступления k-вызова на прибор и завершающееся моментом ухода его из модели.
, - среднее (условно) стационарное время пребывания
k-вызова на приборе, т.е. среднее время, начинающееся с момента первого
поступления k-вызова на прибор и завершающееся моментом ухода его из модели.![]()
![]() , и
, и ![]()
![]()
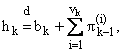
![]() одинаково распределены с периодом
занятости обслуживанием
одинаково распределены с периодом
занятости обслуживанием
![]() -вызовов (1- вызовов, ..., (k-1)-вызовов); vk - случайное число
-вызовов (1- вызовов, ..., (k-1)-вызовов); vk - случайное число
![]() -вызовов, поступающих в
модель за bk, не зависящее от {
-вызовов, поступающих в
модель за bk, не зависящее от {![]() }.
}. ![]() -вызовов. Pk-1 совпадает со средним
периода занятости модели M |G|1|Ґ с
параметром sk-1
поступления и с ФР
-вызовов. Pk-1 совпадает со средним
периода занятости модели M |G|1|Ґ с
параметром sk-1
поступления и с ФР ![]()
![]() потоки (k + 1)-вызовов, ..., r-вызовов не влияют на
величины Wi и Hi, i =
потоки (k + 1)-вызовов, ..., r-вызовов не влияют на
величины Wi и Hi, i =![]() , то
для абсолютных с дообслуживанием приоритетов из (3) и (7) следует система
уравнений
, то
для абсолютных с дообслуживанием приоритетов из (3) и (7) следует система
уравнений ![]()
![]()
![]()
![]()
![]() Mw(t) (см.,
например, [2]) и стационарные Nk, Tk и Myk,
k =
Mw(t) (см.,
например, [2]) и стационарные Nk, Tk и Myk,
k =![]() , то, переходя к пределу t ® +Ґ в (12), с учетом
P{Tk = 1} = MTk и (11), получаем
, то, переходя к пределу t ® +Ґ в (12), с учетом
P{Tk = 1} = MTk и (11), получаем ![]() .
.