МАТЕМАТИКА
УДК 517.518.8, 517.538.3, 517.982
Академик А. Б. Нерсесян
Об одном обобщении аппроксимации Паде
(Представлено 25/VI 2003)
1. Схема для бесконечных рядов
1.1. Рассмотрим Банахово
пространство B над полем комплексных чисел и некоторый базис {an} (n = 0, 1, 2, ...) в нем.
Пусть задан степенной ряд (производящая
функция системы {an})
| g(w) = |
Ґ
е
n=0
|
gn wnan, {gn}
М C, w О C, | |
(1) |
сходящийся при |w| < Rg (0 <
Rg Ј Ґ) и
gn № 0 при n і
Ng.
Для произвольного f О B, f =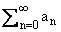 an, и целого N і 0 обозначим
an, и целого N і 0 обозначим
| SN(f) = |
N-1
е
n=0
|
anan,
RN(f) = |
Ґ
е
n=N
|
anan. | |
(2) |
Таким образом,
f = SN(f) + RN(f). Согласно формуле суммирования по частям
Абеля имеем
| RN(f) = |
Ґ
е
n=N
|
bnbn = bNw-N |
Ґ
е
k=N
|
wkbk + |
Ґ
е
n=N
|
(bn+1 - bnw)w-n-1 |
Ґ
е
k=n+1
|
wkbk, | |
(3) |
где
bn = an/gn, bn = gnan, n і Ng и w
О C, w № 0, |w| < Rg.
Для заданного конечного множества комплексных чисел {wk},
wk № 0, |wk| < Rg,
k = 1, 2, ..., m, введем в рассмотрение следующие рекуррентно определяемые
последовательности:
Dn0 = bn,
Dnk =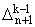 - wkDnk-1, n і N, 1 Ј k
Ј m - wkDnk-1, n і N, 1 Ј k
Ј m | |
(4) |
| U1(n,k) = w11, Up(n,k) = |
k-p+1
е
s=n+1
|
|
ж
з
и |
wp
wp-1
|
ц
ч
ш |
s
|
Up-1(s,k) | |
| 2 Ј p Ј m, n і
N - 1, k і N + p. | |
(5) |
Теорема 1. При N і Ng справедлива следующая
формула
|
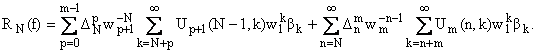
|
(6) |
Наметим схему доказательства. Пусть m
= 2 и в формуле (3)
w = w1. Применив снова формулу Абеля соответствeнно выбору
w = w2, (выбрав Dn1
вместо bn) и изменив порядок суммирования в последней двойной сумме,
без труда придем к формуле (6) при m = 2. Повторив этот процесс по индукции, добавляя значения
wk (k = 3, 4, ...,
m) и учитывая соотношения (4) и (5) придем к
формуле (6).
В случаe m = 2 и w2 № w1 имеем
| RN(f) = bNrN(w1) + DN1 |
rN(w1) - rN(w2)
w1 - w2
|
+ |
Ґ
е
n=N
|
Dn2 |
rn+1(w1) - rn+1(w2)
w1 - w2
|
, | |
(7) |
где обозначено
| rn(w) = w-n |
Ґ
е
k=n
|
wkbk = w-n(g(w) - |
n-1
е
k=0
|
wk gkak), n і Ng, |w| <
Rg. | |
(8) |
Если же w2 = w1, то
выражение (rn(w1) - rn(w2))(w1 - w2)-1 надо
заменить производной rnў(w1). Добавляя последовательно значения
w3, w4, ..., wm, мы придем к видоизмененной
формуле (6), содержащей значения функции rn(w) и (если
встречаются величины wk = wp, k № p) ее производных в точках {wk}. Можно показать,
что результат не зависит от нумерации множества {wk}. Эти рассуждения
одновременно доказывают сходимость всех рядов, фигурирующих в формуле (7).
1.2. Поясним метод
аппроксимации, основанный на теореме 1, в простейшем случае m = 1 . Из (2), (3),
(8) легко получить следующую формулу
| f = |
N-1
е
n=0
|
(an - bNw1n-Ngn)an + bNw1-Ng(w1) + |
Ґ
е
n=N
|
Dn1rn(w1). | |
(9) |
Пусть bN № 0 и bN+1 № 0. Выберем
w1 так, чтобы величина |DN1| = |bN+1 - wbN| была возможно малой (если |bN+1/bN| <
Rg, то DN1 = 0, т.е.
w1 = bN+1/bN). Естественно ожидать, что при таком
выборе бесконечный ряд в конце формулы (9) будет стремиться к нулю при N ® Ґ быстрее, чем RN(f) и, отбросив его и учитывая
оставшуюся часть, можно рассчитывать получить лучшее приближение к f, чем
SN+1(f), использовав при этом тот же набор коэффициентов
{ak}, k = 0, 1, ..., N.
Повторив подобные рассуждения на основе
формул (4) и (6), придем к аппроксимационной схеме, основанной на решении линейной алгебраической
системы (если оно существует)
| Dpm = 0,
p = N + 1, N + 2, ..., N + m, | |
(10) |
относительно величин
|
е
n1 < n2 < ... <
nk
|
|
k
Х
i=1
|
wni,
k = 1, 2, ..., m. | |
(11) |
Нетрудно видеть, что система
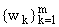 определяется отсюда как множество
корней (с учетом их кратности) полинома с коэффициентами (11).
определяется отсюда как множество
корней (с учетом их кратности) полинома с коэффициентами (11).
Соответственно измененная формула (9) уже будет содержать под знаком бесконечной суммы только сомножители Dnm (n = N + m + 1, N + m + 2, ...), и, отбросив эту сумму, получим приближенное представление функции f с
использованием коэффициентов {a0, a1, ..., aN+2m-1}, {g0, g1, ...,
gN+2m-1} и линейной комбинации значений
производящей функции g(w) на множестве {wk}, k = 1, 2, ..., m (и ее производных, если некоторые точки этого множества совпадают).
Ограничения можно несколько ослабить,
потребовав, чтобы система (10) имела вид Dpm = 0, p = N + 1,
..., N + p, p і m , а задача состояла в минимизации
взвешенной среднеквадратичной ошибки на основе псевдообратной матрицы.
На основе ряда в конце формулы (6) можно, поменяв порядок суммирования, использовать ту же схему, но уже для новой
производящей функции и нового числа m.
Замечание 1. Приведенная схема применима и
в случае "двухстороннего" базиса {an},
n = 0, ±1, ±2, ... в B.
Именно, в этом случае любой элемент f =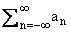 an
можно представить в виде f =
an
можно представить в виде f =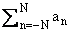 an + RN+ + RN-, где RN+ =
an + RN+ + RN-, где RN+ =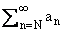 an, RN- =
an, RN- =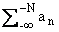 an.
Следовательно, по предлагаемой схеме можно использовать две производящие
функции g±(w).
an.
Следовательно, по предлагаемой схеме можно использовать две производящие
функции g±(w).
Теорема 1 легко обобщается и в случае, когда
в (1) и (2) фигурируют операторные (например, матричные) коэффициенты.
2. Схема для интегральных преобразований
2.1. Континуальный
аналог вышеприведенного метода также можно рассматривать в банаховом
пространстве, но мы остановимся лишь на интегральных преобразованиях функций на
полуоси (0, Ґ), наметив схему эвристически. Примеры
таких преобразований общего вида можно найти, например, в [5,6].
Рассмотрим следующее формальное интегральное преобразование:
| f(x) = |
у
х |
Ґ
0
|
K(x, l) a(l) dl, | |
(12) |
определенное для x і 0. Заданное ядро K(x, l) и функция
a(l) комплекснозначные и достаточно гладкие по l при l > A0 > 0 .
Пусть нам известно некоторое преобразованиe
вида (аналогично (1) назовем его производящей функцией)
| G(x, w) = |
у
х |
Ґ
0
|
K(x, l)e-wlg(l) dl, | |
(13) |
заданного для Re(w) > Rg = const і -Ґ и удовлетворяющего условию
g(l) № 0 при l і A0 = const. Задавшись
положительным A і A0 и обозначив, аналогично
(2),
f = SN(f) + RN(f), где
| SA(f) = |
у
х |
A
0
|
K(x, l)a(l) dl,
RA(f) = |
у
х |
Ґ
A
|
K(x, l)a(l) dl,
| |
(14) |
интегрированием по частям получим
следующий аналог формулы (3)
|
|
|
| RA(f) = h(A)ewA |
у
х |
Ґ
A
|
Q(x, l)e-wldl + | |
|
|
|
| |
у
х |
Ґ
A
|
(hў(l) + wh(l))ewl |
у
х |
Ґ
l
|
Q(x, m)e-wm dm dl, | |
|
|
|
|
|
|
(15) | |
где использованы
обозначения h(l) = a(l)/g(l), Q(x, l) = K(x,
l)g(l).
Для заданного множества комплексных чисел
{wk}, Rewk >
Rg, k = 1, 2, ..., m введем следующие величины (аналогичные (4)
и (5)):
|
|
|
|
|
|
|
| Dk(l) = |
d
dl
|
Dk-1(l) + wkDk-1(l), 1 Ј
k Ј m. | |
(16) | |
| V1(l,m) = 1, Vp(l,m) = |
у
х |
m
l
|
e(wp-1-wp)tVp-1(t,m)dt, 2 Ј p
Ј m | |
(17) |
Аналог теоремы 1 легко доказывается
по индукции, интегрированием по частям.
Теорема 2. При A і A0 справердлива формула
| RA(f) = |
m-1
е
p=0
|
Dp(A)ewm A |
у
х |
Ґ
A
|
Q(x,m)e-w1mVp+1(A,m)dm + | |
|
у
х |
Ґ
A
|
Dm(l)ewml |
у
х |
Ґ
l
|
Q(x,m)e-w1mVm(l,m)dmdl | |
(18) |
2.2. Остальные
построения континуального случая также аналогичны случаю бесконечных рядов. Так,
при m = 2 и w2 № w1 из (18) получим
|
|
|
| RA(f) = h(A)r(x,A,w1) + D1(A) |
r(x, A,
w2) - r(x, A, w1)
w1 - w2
|
+ | |
|
|
|
|
e(w1-w2)A |
у
х |
Ґ
A
|
D2(l) |
r(x, l, w2) - r(x, l, w1)
w1 - w2
|
dl, | |
(19) | |
где обозначено
| r(x, l, w) = ewl |
у
х |
Ґ
l
|
Q(x,m)e-wldm = ewl(G(x,
w) - |
у
х |
l
0
|
K(x, m)e-wmg(m) dm). | |
(20) |
При w2=w1 в
(19) уже фигурируют производные функции G по w. Соответствующую схему аппроксимации
также естественно связать с решением линейной системы с Ганкелевой матрицей
|
dp
dAp
|
Dm(A) = 0,
p = 0, 1, ..., m - 1, | |
(21) |
относительно величин (11), что позволяет найти величины {wk}, в качестве нулей соответствующего
полинома. Естественно рассчитывать на то, что в последнем интеграле формулы (18) функция Dm(l)
(l і A) будет стремиться
к нулю при l ® Ґ достаточно быстро, чтобы,-после отбрасывания этого
интеграла и учета оставшейся части RA(f),- соответствующая
аппроксимация функции f(x) была лучшей, чем SN+m-1(f) .
Практическая реализация может быть основана
на замене производных в (21) соответствующими конечными разностями. Как и выше
вместо (21) можно использовать соответствующую переопределенную систему.
Наконец, исходя из представления (18), можно снова применить ту же схему, но уже
на основе другой производящей функции.
В простейшем случае m = 1 из (15) и (20) следует приближенная формула
| f(x) » |
у
х |
A
0
|
K(x, l) [a(l) - a(A)
ew1(A-l)g(l)/g(A)] dl + h(A)ew1AG(x,
w1). | |
(22) |
Замечание 2. Kак и в дискретном случае, для двухсторонних преобразований (т.е. при
интегрировании в (12) от -Ґ до +Ґ) нужно иметь две производящие функции G±(x, w), соответствующие положительной и отрицательной
полуосям.
3. Заключение
Нетрудно видеть, что в частном случае
аналитической в круге |z|
Ј R функции f(z) = еanzn (базис an = zn определяется равномерной в этом
круге метрикой) и производящей функции g(w) = (1-wz)-1
(gn = 1, n = 0, 1, ...; Rg = R-1) вышеизложенная схема совпадает со схемой
классической аппроксимации Паде (см. [1-3]), отличаясь от нее чисто методически.
Широкий выбор даже элементарных производящих функций открывает новые
возможности.
Известные в случае функциональных рядов
обобщения аппроксимации Паде, в основном, относятся к рациональным приближениям
и основаны на иных подходах (см. [1-3] ). Схема данной работы непосредственно
обобщает также метод Бейкера - Гаммеля для аппроксимации функций марковского
типа (см. [1]) и "сингулярный метод Фурье - Паде" ([6]), который основан на
применении логарифмических производящих функций в случае рядов Фурье. Отметим,
что метод матричных (операторных, см. [1]) аппроксимаций Паде также обобщается
(см. выше Замечание 1).
Что же касается интегральных преобразований,
то предлагаемый метод, по-видимому, совершенно нов, а его эффективность (по
крайней мере, в классических случаях) основана на минимизации величины А (см,
выше (14)) при заданной точности, что позволяет уменьшать осцилляцию подынтегральных
функций, повышая эффективность применения численного интегрирования.
Численная реализация описанных аппроксимаций
оказалась вполне эффективной как в случае разложений Фурье и по классическим
ортогональным полиномам (с использованием стандартных производяших функций), так
и для преобразований Фурье и Ганкеля.
Важно отметить, что и в случае классических
функциональных рядов, и в случае важнейших известных интегральных преобразований
метод данной работы, как правило, позволяет автоматически (численно) приближенно
распознавать сингулярности разлагаемой функции на основе анализа множества
{wk}. За исключением немногочисленных работ (см., например, [7,8]),
эта задача, чрезвычайна важная для приложений, до последнего времени решалась
физически, т.е. сканированием соответствующих графиков (см., например, [9] с
библиографией).
В заключение подчеркнем, что,- в практическом
плане,- производящие функции (1) и (13) должны обладать алгоритмом быстрого и
точного вычисления (например, выражаться через известные элементарные или
специальные функции).
Работа выполнена в рамках проекта ISTC A-823.
Институт математики НАН РА
Литература
1. Бейкер Дж., Грейвс-Моррис
П., Аппроксимации Паде. Мир. Москва.
1986.
2. Lubinsky D. S., Sidi
A.- Trans. Amer. Math. Soc. 1983 V. 278. N 1. P.
333-345.
3. Суетин С. П. -
Успехи мат. наук. 2002. Т. 57. Вып. 1(343). С.
45-142.
4. Рисс Ф., Секефальви-Надь Б. Лекции по функциональному анализу. М. Мир.
1979.
5. Бейтмен Г., Эрдейи А.-
Высшие трансцендентные функции. Т. 2. М. Наука.
1974.
6. Driscoll T. A.,
Fornberg B.- Numerical Algorithms 2001. V. 26. P.
77-92.
7. Eckhoff K. S.- Math. Comput. 1993. V. 61 N 204. P. 745-763.
8. Eckhoff K. S.- Math. Comput. 1995. V. 64
N 210. P. 671-690.
9. Kvernadze G.- Appl. and Comp. Harmonic Analysis. 2001. N
11. P. 439-454.
![]() - wkDnk-1, n і N, 1 Ј k
Ј m
- wkDnk-1, n і N, 1 Ј k
Ј m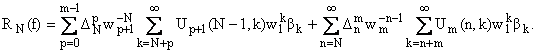
![]() определяется отсюда как множество
корней (с учетом их кратности) полинома с коэффициентами (11).
определяется отсюда как множество
корней (с учетом их кратности) полинома с коэффициентами (11).
![]() an
можно представить в виде f =
an
можно представить в виде f =![]() an + RN+ + RN-, где RN+ =
an + RN+ + RN-, где RN+ =![]() an, RN- =
an, RN- =![]() an.
Следовательно, по предлагаемой схеме можно использовать две производящие
функции g±(w).
an.
Следовательно, по предлагаемой схеме можно использовать две производящие
функции g±(w).