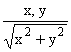Решение задач по дифракционному излучению - предмет математической физики, круг точно решаемых задач весьма ограничен, и поэтому важно разработать приближенный, простой и эффективный метод расчета дифракционного излучения. В работах [2,3] предложен такой метод, справедливый для релятивистских скоростей заряда (b = [v/c] ~ 1), малых углов излучения (q << 1) и длин волн l, малых по сравнению с характерными размерами a препятствий (l << a).
Рассмотрим дифракционное излучение, возникающее при пролете заряда через центр круглого отверстия радиуса a в бесконечном плоском проводящем экране. Начало координат выберем в центре отверстия, плоскость отверстия (и экрана) совместим с плоскостью z = 0, скорость заряда v направим вдоль оси z.
В работе [2] показано, что Фурье - образ монохроматической компоненты поля излучения
|
(1) |
где интегрирование ведется по части
плоскости z = 0, занятой экраном,
![]() =[(w)/c]
=[(w)/c]![]() - волновой вектор,
- волновой вектор,
![]() - направление излучения,
- направление излучения,
![]() - радиус-вектор в
плоскости z = 0,
- радиус-вектор в
плоскости z = 0,
|
(e
- заряд частицы, K1(ar) - функция Макдональда).
(В [4,5], используя формулу (1) и ссылаясь при этом на книгу [1],
допускается неточность - утверждается, что в (1) интегрирование ведется по
площади отверстия. Эта неточность, как нам кажется, является результатом
невнимательности и того факта, что авторы работ [4,5], по-видимому, не были
знакомы с оригинальными работами [2,3], в которых четко говорится об
интегрировании по площади экрана).
Интегрируя
в (1) с использованием формулы (см.[6])
|
(2) |
|
(3) |
где q = [(w)/c]q, Jn(qa) - функции
Бесселя. Формула (3) определяет также и поляризацию излучения - электрический
вектор лежит в плоскости (![]() ).
).
При
фиксированной частоте w и угле излучения q формулой (3) определяется зависимость Ex от
радиуса отверстия a. Наличие J0(x) и J1(x) означает, что с
изменением аргумента этих функций происходят колебания значений Ex.
Следовательно, при изменении радиуса а будем иметь усиление и ослабление
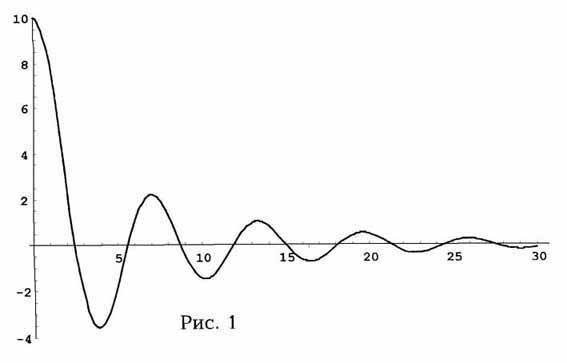
интенсивности излучения. Что это действительно так, видно из рис. 1, где
приведен график функции f(x) при p = 10-1, где
|
(здесь
x = qa, p = [(a)/q] = (bgq)-1 » (gq)-1).
Нам понадобятся
еще и точки экстремума функции f(x), чтобы определить те значения радиуса
отверстия a, при которых поле излучения Ex будет иметь большие
значения. Вычислив fў(x) = -(1 + p2)xJ1(x)K1(px) и
приравняв fў(x) нулю, получим, что искомые
значения ai определяются из условия J1(xi) = 0,
i = 0,1,2,3,..., т.е. ai = [(xi)/q], где xi - нули
функции J1(x).
Учитывая
приведенную на рис.1 зависимость поля излучения от радиуса отверстия, а также
тот факт, что при нахождении полей излучения производится интегрирование по
площади экрана, приходим к выводу, что можно добиться усиления дифракционного
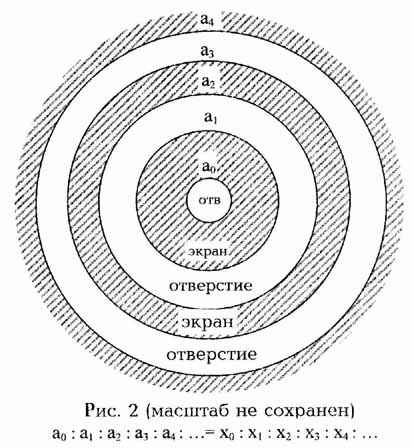
излучения, если заряд будет пролетать через кольцевую "дифракционную решетку" -
систему отверстий и экранов в виде концентрических колец-экранов с радиусами
(a0,a1), (a2,a3),
(a4,a5) и т.д. (см.рис.2). (Следует особо подчеркнуть, что
хотя и a0 должно равняться нулю (т.к. x0 = 0), мы будем
считать a0 № 0 (и поэтому x0
№ 0), но близко к нулю настолько, что условие l << a0 можно считать выполненным). Считая
a0 отличным от нуля, мы увеличиваем долю дифракционного излучения за
счет первого края радиуса a0 первого кольца, наиболее близкого от
траектории пролета заряда, где (у этого края) напряженность поля частицы больше;
если a0 = 0, то отсутствует отверстие радиуса a0,
отсутствует дифракционное излучение на этом отверстии и вместо дифракционного
имеем, например, переходное излучение при пересечении зарядом
экрана.
|
|
Чтобы оценить эффективность действия
системы колец, посчитаем интенсивность дифракционного излучения Sw , возникающего при пролете заряда через центр системы
на рис.2, и сравним ее с излучением S0w в
случае пролета через центр одного отверстия радиуса a0 в бесконечном
экране. Поскольку спектральная плотность излучения в единицу телесного угла
определяется формулой
|
то
для сравнения достаточно посчитать отношение (обозначим его через N) полей
излучения. Используя формулы (1) и (2), проинтегрировав по площадям
колец-экранов, найдем
|
(4) |
Так как функция
Ki(pxi) очень быстро спадает и отлична от нуля практически
только при pxi ~ 1, то в сумме можно
ограничиться лишь несколькими слагаемыми.
Исходя из формулы (4), оценим теперь величину N для случаев
p1 = 10-1 и
p2 = 10-2. Выбор этих значений p
< 1 обусловлен тем, что чем меньше параметр p, тем точнее приближенная
формула (1) [см. 2] и тем больше значение f(x0), т.е. в конечном
итоге интенсивность дифракционного излучения. Ограничиваясь лишь четырьмя
слагаемыми в (4) и подставляя нули функции J1(x): x1 = 3.83;
x2 = 7.016; x3 = 10.17; x4 = 13.32, из [7]
находим
N1 = 1.94
(при p1 = 10-1,
q = 10-2,
x0 = 0.5),
N2 = 2.24
(при p2 = 10-2,
q = 10-2,
x0 = 0.5).
Все параметры нужно взять
из опыта, а параметр x0 - из соответствующего графика функции f(x),
но так, чтобы выполнялись условия a0 << l и применимости приближенного
метода.
|
|
Таким образом, использование системы
концентрических экранов приводит к усилению дифракционного излучения более чем в
N12 » 3.7 раза при
p1 = 10-1 и более чем в
N22 = 5 раз в случае p2 = 10-2. Это означает, что система (рис.2) ведет себя как
своеобразная зонная пластинка Френеля и величины a0,a1...
являются как бы аналогами радиусов зон Френеля.
Меняя длину волны l и угол q (при неизменном q = [(2pq)/(l)]), можно использовать
пластинку для других длин волн, но наблюдая усиление под иными углами.
Ереванский государственный университет