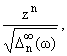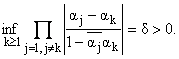МАТЕМАТИКА
УДК 517.53
А. М. Джрбашян
О весовых пространствах целых функций, суммируемых по
комплексной плоскости
(Представлено академиком В. С. Захаряном 2/V 2003)
Статья усиливает результаты М. М. Джрбашяна
[1] о весовых пространствах целых функций, интегрируемых по площади всей
комплексной плоскости. Даны теоремы представления во сколь угодно широких
банаховых пространствах целых функций. Полученная явная формула для изометрии
между пространством Харди H2 и рассматриваемыми пространствами
позволяет преобразовывать известные в H2 предложения в такие же
предложения во сколь угодно широких гильбертовых пространствах целых функций.
Статья является продолжением работы [2].
1. Представления во
всей комплексной плоскости.
1.1. Ниже мы будем рассматривать пространства
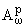 (C) (1
Ј p < +Ґ) целых функций
F(z), удовлетворяющих условию
(C) (1
Ј p < +Ґ) целых функций
F(z), удовлетворяющих условию
| ||F||p,w = |
м
н
о |
1
2p
|
|
уу
ххC |
|F(z)|p|dmw(z)| |
ь
э
ю |
1/p
|
< +Ґ, | |
где
dmw(reiJ) = -dw(r2)dJ, а w О WAҐ, т.е.
функция w(x) строго убывает на всей полуоси [0,+Ґ) и такова, что w(0) = 1 и
| DnҐ(w) = - |
у
х |
+Ґ
0
|
tndw(t)
< +Ґ при n = 0,1,2ј | |
Через
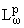 (C) будем
обозначать соответствующие лебеговы пространства.
(C) будем
обозначать соответствующие лебеговы пространства.
Лемма 1.1.
При любом p О [1,+Ґ) сумма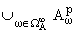 (C) совпадает со множеством всех
целых функций.
(C) совпадает со множеством всех
целых функций.
1.2. Заметив, что при вышеприведенных условиях limn®Ґ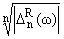 = R2 при DnR(w) = -т0R2tn|dw(t)| и
любом R О (0,+Ґ], приведем
сначала следующую теорему о представлениях.
= R2 при DnR(w) = -т0R2tn|dw(t)| и
любом R О (0,+Ґ], приведем
сначала следующую теорему о представлениях.
Теорема 1.1.
Пусть F(z) О Aw2(C) (w О WAҐ). Тогда в
любой точке z О C
| F(z) = |
1
2p
|
|
уу
ххC |
F(z)CwҐ(z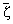 )dmw(z) = - )dmw(z) = -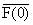 + + |
|
1
p
|
|
уу
ххC |
{Re F(z)} |
CwҐ(z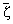 )dmw(z), )dmw(z), |
|
где
CwҐ(z) = еn=0Ґ zn/DnҐ(w) - ядро типа Коши из [3].
Замечание 1.1. При w О WAҐ множество функций
en(z) =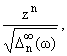 |
n = 0,1,2,... | |
является
ортогональным базисом пространства Aw2(C). Кроме того,
справедлива
Теорема 1.2. Если w О WAҐ, то для
ортогональной проекции Lw2(C) на Aw2(C) верна формула
| Pwf(z) = |
1
2p
|
|
|
уу
ххC |
f(z) CwҐ(z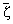 )dmw(z), z О C, f
О Lw2(C). )dmw(z), z О C, f
О Lw2(C). |
|
1.3. При параметр-функциях w(x) определенного типа следующая теорема устанавливает явные
предствления для действующего между пространством H2 Харди и
Aw2(C)
изометрического оператора и его обратного.
Теорема 1.3.
Пусть функция w О WAҐ непрерывно
дифференцируема в [0,+Ґ) и такова, что w(+Ґ) = 0, производная wў(x) < 0 и ограничена в
[0,+Ґ), а также
Тогда функция
|
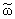 (x) = - (x) = - |
у
х |
+Ґ
0
|
w |
ж
и |
|
x
t
|
|
ц
ш |
dw(t), 0 < x
< +Ґ, | |
принадлежит
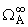 , и
, и
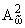 (C) совпадает со множеством всех функций, представимых в виде
(C) совпадает со множеством всех функций, представимых в виде
| F(z) = |
1
2p
|
|
у
х |
2p
0
|
j(eiJ) CwҐ(ze-iJ) dJ, z О C, j(eiJ) О L2[0,2p]. | |
(1.1) |
Для любого F(z) О
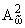 (C)
существует единственная функция j0(z) О H2 такая, что (1.1) верно с j0(eiJ). Эта
функция задается формулой
(C)
существует единственная функция j0(z) О H2 такая, что (1.1) верно с j0(eiJ). Эта
функция задается формулой
| j0(z) = LwҐ
F(z) = - |
у
х |
+Ґ
0
|
F(tz)dw(t), |z| <
1. | |
Кроме того, ||j0||H2 = ||F||2,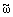 , и j-j0 ^ H2 для
любого j(eiJ) О L2[0,2p], с которым
верно (1.1). Оператор Lw является изометрией
, и j-j0 ^ H2 для
любого j(eiJ) О L2[0,2p], с которым
верно (1.1). Оператор Lw является изометрией
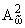 (C) ® H2, и интеграл (1.1)
задает (Lw)-1 на
H2.
(C) ® H2, и интеграл (1.1)
задает (Lw)-1 на
H2.
Замечание 1.2. Пространства
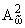 (C), рассматриваемые в теореме 1.3, исчерпывают все целые
функции.
(C), рассматриваемые в теореме 1.3, исчерпывают все целые
функции.
1.4. В
общем случае 1 Ј p < +Ґ
верна следующая теорема о представлении функций из
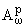 (C) интегралом по окружности
|z|=1.
(C) интегралом по окружности
|z|=1.
Теорема
1.4. Пусть 1 Ј p < +Ґ, w(x) О
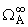 и
и
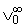 w = 1. Тогда любая функция F(z) О
w = 1. Тогда любая функция F(z) О
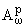 (C)
представима в виде
(C)
представима в виде
| F(z) = |
1
2p
|
|
у
х |
2p
0
|
Cw1(ze-iJ)j(eiJ)dJ, |z| <
1, | |
(1.2) |
где w1(x) = w(x2), а
j(z) = Lw1F(z) О
Hp. При этом ||Lw1|| Ј 1 в
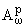 , и
(1.2) задает Lw1-1 на множестве Lw1
, и
(1.2) задает Lw1-1 на множестве Lw1
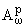 (C).
(C).
1.4. Особо отметим, что утверждения теоремы 1.3 верны, когда
wў(x) = -C0 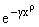 xmr-1 (0 < x < +Ґ, g,r,m >
0), C0= xmr-1 (0 < x < +Ґ, g,r,m >
0), C0= |
й
л |
у
х |
+Ґ
0
|
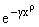 xmr-1dx xmr-1dx |
щ
ы |
-1
|
, | |
несмотря на то, что
в этом случае не выполнены условия на
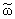 ў(x), обеспечивающие включение w(x)
О
ў(x), обеспечивающие включение w(x)
О
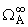 теоремы 1.3. А именно, имеет место следующее усиление
теоремы XIV1 из [1].
теоремы 1.3. А именно, имеет место следующее усиление
теоремы XIV1 из [1].
Теорема 1.5. Гильбертово пространство целых
функций, определенных условием
| ||F|| = |
м
н
о |
1
2p
|
|
у
х |
+Ґ
0
|
dJ |
у
х |
2p
0
|
|F(reiJ)|2e-2grrr2mr-r/2-1dr |
ь
э
ю |
1/2
|
< +Ґ, | |
(1.3) |
где g,r,m >
0 - любые числа, совпадает со множеством всех функций, представимых в виде
| F(z) = |
rgm
2p
|
|
у
х |
2p
0
|
Er(g1/rze-iJ,m)j(e-iJ)dJ, z О
C, j(e-iJ) О
L2[0,2p], | |
(1.4) |
где
| Er(z,m) = |
Ґ
е
k=0
|
|
zk
G(m+k/r)
|
| |
-
общеизвестная функция типа Миттаг-Леффлера.
Для любого F(z) из пространства (1.3) существует единственная функция
j0(z) О
H2 такая, что (1.4) верно с j0(eiJ). Эта
функция задается формулой
| j0(z)= |
у
х |
+Ґ
0
|
F(tz)e-gtrtmr-1dt, |z| <
1. | |
Кроме того, ||j0||H2 = ||F||, и j - j0 ^ H2 для любого j(e-iJ) О L2[0,2p], с которым верно
(1.4).
2.
Биортогональные системы функций в A2w.
Установленные в теоремах 1.3 и 1.5 формулы для изометрий между
H2 (|z| < 1) и
пространствами
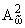 (C) предоставляют
возможность легко переводить известные в пространстве Харди H2 факты
в аналогичные предложения в
(C) предоставляют
возможность легко переводить известные в пространстве Харди H2 факты
в аналогичные предложения в
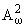 (C). 1 В частности, результаты М. М. Джрбашяна и Г. М.
Айрапетяна [4-6] о биортогональных системах функций в
H2 переводятся в аналогичные утверждения для
(C). 1 В частности, результаты М. М. Джрбашяна и Г. М.
Айрапетяна [4-6] о биортогональных системах функций в
H2 переводятся в аналогичные утверждения для
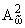 (C).
(C).
Мы будем рассматривать
случай простых узлов интерполяции, т.е. будем полагать, что {aj}1Ґ - последовательность попарно различных чисел в |z| < 1, подчиненная условию
Бляшке
Далее, будем полагать, что {aj}1Ґ О D, если последовательность {aj}1Ґ равномерно отделена, т.е.
|
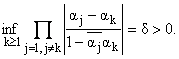
|
Введем также произведение Бляшке с нулями в {aj}1Ґ:
Полагая, что всюду ниже функции
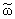 (x)
и w(x) таковы, как в теореме 1.3 либо в теореме 1.5,
для изометрий H2 ®
(x)
и w(x) таковы, как в теореме 1.3 либо в теореме 1.5,
для изометрий H2 ®
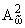 (C) этих теорем введем
обозначение
(C) этих теорем введем
обозначение
| TwҐ(f(z)) = |
1
2p
|
|
у
х |
2p
0
|
f(eiJ)CwҐ(zeiJ)dJ, |z| <
1, (Tw = (LwҐ)-1). | |
Тогда хорошо известное неравенство Шапиро - Шилдса [7] запишется в
нижеприводимом виде.
Предложение 2.1. Если {ak}1Ґ О D, то для любого F(z) О
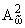 (C)
(C)
|
Ґ
е
j=1
|
(1-|aj|2)|LwҐF(aj)|2 Ј C||F||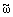 ,
2, ,
2, | |
где C -
постоянная.
Ниже приведем ряд
предложений, в основном следуя порядку изложения [6]. Однако сначала обозначим
|
|
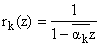 Wk(z) = Wk(z) = |
B(z)
z-ak
|
. | |
Далее, отметим
следующие формулы для систем целых функций TwҐ(rk(z)) =
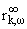 (z) и TwҐ(Wk(z)) =
(z) и TwҐ(Wk(z)) =
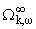 (z) (k = 1,2,ј):
(z) (k = 1,2,ј):
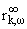 (z) = (z) =
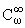 |
(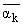 z) и z) и 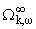 (z) = (z) = |
lim
r®1-0
|
|
Ґ
е
n=0
|
|
znrn
Dn(w)
|
|
Ґ
е
m=0
|
akmrm+1bn+m+1, | |
(2.2) |
где bn - коэффициенты
разложения B(z) =
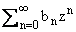 (|z| < 1).
(|z| < 1).
Предложение 2.2. Если последовательность {ak}1Ґ не подчинена условию Бляшке, т.е. ряд (2.1)
расходится, то обе системы (2.2) полны в
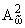 (C).
(C).
Теперь через
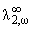 {ak} обозначим
множество всех функций F(z) О
{ak} обозначим
множество всех функций F(z) О
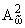 (C), для которых
граничные значения LwҐ F(z) почти всюду на |z|=1 совпадают с граничными значениями y(z)/ B(1/z) для некоторых y(z)
О H2, y(0) = 0.
(C), для которых
граничные значения LwҐ F(z) почти всюду на |z|=1 совпадают с граничными значениями y(z)/ B(1/z) для некоторых y(z)
О H2, y(0) = 0.
Предложение 2.3. Функции систем (2.2) принадлежат
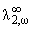 {ak}, и системы
(2.2) биортогональны в
{ak}, и системы
(2.2) биортогональны в
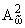 (C), т.е.
(C), т.е.
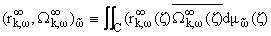 |
= |
м
н
о |
|
| |
Предложение 2.4. Пусть F(z) О
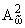 (C). Тогда F(z) О
(C). Тогда F(z) О
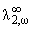 {ak} в том и только том случае, когда
{ak} в том и только том случае, когда
|
у
х |
|z|=1
|
|
LwҐ
F(z)
B(z)
|
|
dz
z-z
|
є
0, z О C. | |
Предложение 2.5.
Любая функция f(z)
О
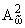 (C) представима в виде
(C) представима в виде
| f(z) = f1(z) + f2(z),
||f||2 = ||f1||2 + ||f2||2, | |
где
f1(z) О
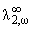 {ak} и
{ak} и
f2(z) = Tw(B(z)g(z)) О
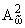 (C), g(z) = (C), g(z) = |
1
2p
|
|
у
х |
|z|=1
|
|
LwҐf(z)
B(z)
|
|
dz
z-z
|
О
H2. | |
Предложение 2.6.
Если {ak}1Ґ О D, а последовательность {wk}1Ґ подчинена условию
|
Ґ
е
k=1
|
(1-|ak|)|wk|2 < +Ґ, | |
то
существует единственная функция F(z) О
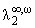 {ak}
такая, что
{ak}
такая, что
| LwҐF(ak)n = wk, k = 1,2,ј | |
(2.3) |
Эта функция представима в виде
| F(z) = |
Ґ
е
k=1
|
wk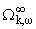 (z), z О C, (z), z О C, | |
где ряд
сходится по норме Aw2. Функция же
F(z) - решение интерполяционной задачи (2.3) с минимальной
нормой.
Предложение
2.7. Множества {(1-|ak|2)1/2
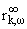 (z)}1Ґ
и
(z)}1Ґ
и
{(1-|ak|2)-1/2
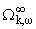 (z)}1Ґ
являются безусловными базисами в
(z)}1Ґ
являются безусловными базисами в
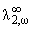 {ak} в том и только том случае, когда {ak}1Ґ О D.
{ak} в том и только том случае, когда {ak}1Ґ О D.
Предложение 2.8. Если {ak}1Ґ О D, то любая функция F(z) О
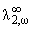 {ak} допускает
разложения
{ak} допускает
разложения
| F(z) = |
Ґ
е
k=1
|
ck(F)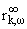 (z) = (z) = |
Ґ
е
k=1
|
LwҐ
F(ak)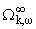 (z), z О C, ck(F) = (z), z О C, ck(F) =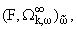 | |
сходящиеся
по норме в
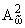 (C).
(C).
Замечание. Рассмотренные выше биортогональные системы качественно
разнятся от тех, которые были рассмотрены А. Ф. Леонтьевым [8].
Институт математики НАН РА
Литература
1. Джрбашян М. М.- Сообщ. Ин-та матем. и мех. АН АрмССР. 1948. Т. 2. С. 3 -
40.
2. Джрбашян А. М., Аветисян
К. Л.- ДНАН Армении. 2002. Т. 102. № 2. С. 105 -
112.
3. Джрбашян М. М.- Изв. АН АрмССР. Математика. 1970. Т. 5. № 6. С. 453 -
485.
4. Джрбашян М. М.- Изв. АН АрмССР. Математика. 1973. Т. 8. № 5. С. 384 -
409.
5. Джрбашян М. М.- Изв. АН Арм. ССР. Математика. 1974. Т. 9. № 5. С. 339 -
373.
6. Айрапетян Г. М.- Изв. АН АрмССР. Математика. 1975. Т. 10. № 2. С. 133 -
152.
7. Shapiro H., Shields A.-
Amer. J. Math. 1961. V. 83. P. 513 -
532.
8. Леонтьев А. Ф. Обобщения рядов экспонент. М. Наука. 1981.
Footnotes:
1Следует отметить, что то же самое верно в отношении
рассмотренных в теореме 1.2 из [2] изометрий между H2 и
пространствами Aw2 в
|z| < 1.
![]() (C) будем
обозначать соответствующие лебеговы пространства.
(C) будем
обозначать соответствующие лебеговы пространства.![]() (C) совпадает со множеством всех
целых функций.
(C) совпадает со множеством всех
целых функций.![]() = R2 при DnR(w) = -т0R2tn|dw(t)| и
любом R О (0,+Ґ], приведем
сначала следующую теорему о представлениях.
= R2 при DnR(w) = -т0R2tn|dw(t)| и
любом R О (0,+Ґ], приведем
сначала следующую теорему о представлениях.![]() (C)
существует единственная функция j0(z) О H2 такая, что (1.1) верно с j0(eiJ). Эта
функция задается формулой
(C)
существует единственная функция j0(z) О H2 такая, что (1.1) верно с j0(eiJ). Эта
функция задается формулой ![]() , и j-j0 ^ H2 для
любого j(eiJ) О L2[0,2p], с которым
верно (1.1). Оператор Lw является изометрией
, и j-j0 ^ H2 для
любого j(eiJ) О L2[0,2p], с которым
верно (1.1). Оператор Lw является изометрией
![]() (C) ® H2, и интеграл (1.1)
задает (Lw)-1 на
H2.
(C) ® H2, и интеграл (1.1)
задает (Lw)-1 на
H2.