МАТЕМАТИКА
УДК 517.55
А. И. Петросян
О весовых классах голоморфных функций в единичном шаре в
Cn
(Представлено академиком В. С. Захаряном 22/IV 2003)
1.
В работе анонсируются
основные результаты общей теории пространств
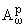 в единичном шаре из
Cn. Рассматриваемые весовые пространства
в единичном шаре из
Cn. Рассматриваемые весовые пространства
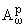 голоморфных в единичном шаре
функций сколь угодно широки, ибо зависят от функции-параметра w(x) (0 Ј x < 1) со сколь угодно
быстрым убыванием при x ® 1 - 0.
голоморфных в единичном шаре
функций сколь угодно широки, ибо зависят от функции-параметра w(x) (0 Ј x < 1) со сколь угодно
быстрым убыванием при x ® 1 - 0.
Приводимые теоремы являются многомерными
w-аналогами результатов М.М. Джрбашяна 1945-1948гг.,
положивших начало теории пространств
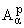 (изначальное обозначение Hp(a)) в единичном круге [1], [2].
(изначальное обозначение Hp(a)) в единичном круге [1], [2].
Примененный аналитический аппарат позволяет
распространить на случай единичного шара одномерную общую теорию, построенную в
[3] (см. также [4]). В работе приведены первые, основные результы, полученные
этим путем.
Следует отметить, что сама теория пространств
Hp(a) М.М. Джрбашяна, относящаяся к частному
случаю w(x) = (1 - x)1+a (a > -1), на случай единичного шара была распространена ранее (см.
[5]). Подробнее о недоразумениях, приведших в [5] и других публикациях западных
авторов к отсутствию надлежащих ссылок на основополагающие работы М.М.
Джрбашяна [1,2] см. в [3].
2. Ниже будем
пользоваться следующими обозначениями:
Bn
= {z О Cn : |z| < 1} - открытый единичный шар в Cn;
Sn = {z О Cn : |z| = 1} - его граница, являющаяся
единичной сферой в Cn;
Всюду ниже число n фиксировано, поэтому мы
будем писать просто B и S вместо Bn и Sn.
n - мера Лебега в Cn, нормированная условием n(B) = 1;
s - борелевская мера
на S, инвариантная относительно унитарных преобразований
пространства Cn и удовлетворяющая условию s(S) = 1.
Через бz,wс =
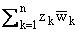 будем обозначать скалярное произведение для
точек z,w О Cn, а через
|z| =
будем обозначать скалярное произведение для
точек z,w О Cn, а через
|z| =
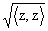 - соответствующую норму.
- соответствующую норму.
С каждым мультииндексом
s = (s1,...,sn) О Z+n, где
будем связывать: два числа s! =
 и |s| =
и |s| =
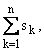
оператор дифференцирования Ds =
[(¶|s|)/(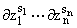 )],
)],
и голоморфный моном zs =
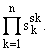
Далее, через W будем
обозначать множество параметр-функций w(t),
определенных на интервале [0,1) и удовлетворяющих там условиям
(i) 0 <
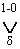 w < Ґ для любого d О [0,1);
w < Ґ для любого d О [0,1);
(ii) Dm є Dm(w) = -т01tmdw(t) № 0, Ґ, m = 0,1,ј;
(iii)
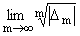 і 1. і 1.
Для удобства всюду ниже будем полагать, что w(1) = w(1 - 0).
3. Для заданного w О W
введем в рассмотрение ядро-функцию
| Cw,n(z,w) = Cw(z,w) = |
е
s О Z+n
|
(n-1+|s|)!
(n-1)!s!
|
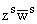
D|s|
|
. | |
(1) |
Предложение 1. При фиксированной точке w О
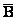 функция Cw(z,w) голоморфна в шаре B.
функция Cw(z,w) голоморфна в шаре B.
Предложение 2. Имеет место равенство
| Cw(z,w) = |
Ґ
е
m=0
|
1
Dm
|
(n-1+m)!
(n-1)!m!
|
бz,wсm, z О B, w О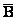 . . |
| Тем
самым, ядро Cw зависит лишь от скалярного
произведения бz,wс.
4. Для каждой функции w О W определим ассоциированную с ней
меру
где
w = rz - полярная форма точки w О B, (т. е. z
О S, 0 Ј
r Ј 1).
Обозначим через
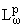 = =
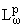 (B) класс функций,
измеримых по мере dmw в шаре B, для которых (B) класс функций,
измеримых по мере dmw в шаре B, для которых
| ||f||p,w = |
м
н
о |
у
х
B
|
|f(w)|p |dmw(w)| |
ь
э
ю |
1/p
|
< +Ґ, 0 < p
< Ґ, | |
(2) |
а через
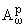 = =
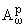 (B) - подмножество (B) - подмножество
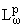 , состоящее из функций,
голоморфных в B. Как известно, при 1 Ј p < Ґ величина ||f||p,w определяет норму в , состоящее из функций,
голоморфных в B. Как известно, при 1 Ј p < Ґ величина ||f||p,w определяет норму в
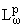 , в которой , в которой
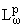 является банаховым пространством, а при 0
< p < 1 является банаховым пространством, а при 0
< p < 1
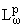 является полным
метрическим пространством в метрике r(f,g) = ||f - g|| является полным
метрическим пространством в метрике r(f,g) = ||f - g||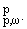
Имеет место следующее
Предложение 3. Пусть 0 < p < Ґ, K -
компакт, лежащий
внутри B. Тогда существует константа C є C(K,s,p,w) такая, что
|
max
z О
K
|
|Dsf(z)|
Ј C||f||p,w | |
(3) |
для всех f О
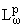 и всех s
О Z+n.
и всех s
О Z+n.
Пусть ||fn -
f||p,w ® 0 при n ®
Ґ
для некоторых fn О
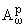 , f О , f О
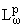 . Из (3) следует, что
существует голоморфная в B функция h(z), такая, что
fn(z) ® h(z) равномерно внутри
B. Нетрудно показать, что f =
h. Тем самым справедливо . Из (3) следует, что
существует голоморфная в B функция h(z), такая, что
fn(z) ® h(z) равномерно внутри
B. Нетрудно показать, что f =
h. Тем самым справедливо
Предложение 4. Для каждого 0 < p <
Ґ подпространство
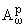 замкнуто в
замкнуто в
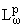 (B). (B).
Следствие. При 1 Ј p < Ґ класс
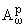 является банаховым
пространством, а при 0 < p < 1 - полным метрическим пространством.
является банаховым
пространством, а при 0 < p < 1 - полным метрическим пространством.
Для произвольной функции f, определенной в B и 0 <
ρ < 1, обозначим
через fρ
ее -растяжение, т. е. функцию, определенную при |z| < 1/ρ
следующим образом: fρ(z) = fρ(z). В следующем
предложении утверждается непрерывность
ρ-растяжения в
пространстве
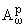 . .
Предложение 5. Если f О
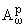 ,
то
||fρ
- f||p,w ®
0 при
ρ
® 1 - 0. ,
то
||fρ
- f||p,w ®
0 при
ρ
® 1 - 0.
Следствие. Голоморфные полиномы плотны в
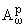 . .
Имеет место основная
Теорема 1. Пусть f О
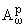 .
Тогда .
Тогда
| f(z) = |
у
х
B
|
f(w)Cw
(z,w)dmw (w),
z О B | |
(4) |
f(z)
= -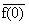 +2 +2 |
у
х
B
|
{Re f(w)}Cw (z,w)dmw
(w), z О B. | |
(5) | Отметим один частный случай формулы (4). Пусть
| w(x)
= n |
1
у
х
x
|
tn-1(1-t)a dt,
(a >
-1). | | Тогда
| Dm
= -n |
1
у
х
0
|
xmdw(x) =
n |
1
у
х
0
|
xn+m-1(1-x)adx = |
nG(n+m)G(1+a)
G(n+m+1+a)
|
. | | Тем
самым ввиду предложения 2 и формулы биномиального разложения
| Cw(z,w) = |
Ґ
е
m=0
|
(n+m-1)!
(n-1)!m!
|
бz,wсm
Dm
|
=
| |
| = |
Ґ
е
m=0
|
G(n+m)
G(n)G(m+1)
|
G(n+m+1+a)
nG(n+m)G(1+a)
|
бz,wсm =
| |
| = |
G(n+1+a)
G(n+1)G(1+a)
|
Ґ
е
m=0
|
G(n+m+1+a)
G(n+1+a)G(m+1)
|
бz,wсm =
| |
| = |
G(n+1+a)
G(n+1)G(1+a)
|
1
(1-бz,wс)n+1+a
|
. | | Далее, если w = rz, где |z| = 1, то, используя выражение для
элемента нормированного объема dn в полярных
координатах [5], получим
| dmw(w) = -dw(r2) ds(z) = 2nr2n-1(1-r2)adr ds(z) = (1-r2)a dn(w). | |
(6) | Отсюда следует, что в
рассматриваемом случае формула (4) принимает вид
| f(z) = |
G(n+1+a)
G(n+1)G(1+a)
|
у
х
B
|
f(w) |
(1-|w|2)a
(1-бz,wс)n+1+a
|
dn(w). | |
Эту
формулу можно найти в [5]. В одномерном же случае n = 1 она впервые была получена
в работе М. М. Джрбашяна [1].
Ядро Cw(z,w) порождает оператор ортогонального проектирования
из
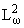 на подпространство на подпространство
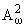 . А именно, имеет место
следующая . А именно, имеет место
следующая
Теорeма 2. Пусть
| Pw f(z) = |
у
х
B
|
f(w)Cw
(z,w) dmw (w), z О B, | |
где f О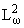 .
Тогда Pw является ортогональным
проектором из .
Тогда Pw является ортогональным
проектором из
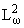 на
на
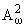 . .
5. Ниже приведено интегральное
представление функций из
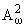 по границе B, в случае, когда w является
квадратом Вольтерра от другой функции
по границе B, в случае, когда w является
квадратом Вольтерра от другой функции
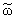 О W. Затем найден некий
изометрический оператор, переводящий О W. Затем найден некий
изометрический оператор, переводящий
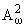 в обычное пространство Харди в B, который вместе со своим обратным
оператором записывается в явном, интегральном виде. Однако сначала следует
отметить, что верно
в обычное пространство Харди в B, который вместе со своим обратным
оператором записывается в явном, интегральном виде. Однако сначала следует
отметить, что верно
Предложение 6. Пусть непрерывно дифференцируемая на [0,1)
функция
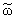 О W такова, что О W такова, что
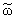 (t) (t) , ,
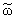 (1)
= 0, (1)
= 0,
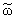 (0) = 1.
Далее, пусть w является квадратом (0) = 1.
Далее, пусть w является квадратом
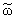 в смысле Вольтерра, т. е.
в смысле Вольтерра, т. е.
Тогда
w О W
и, кроме того,
| Dm(w) = |
й
л |
Dm(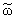 |
) |
щ
ы |
2
|
, m і 0. | |
(7) | Теорема 3.
Если функция f принадлежит
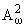 ,
то функция ,
то функция
j0(z) = L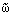 f(z) = - f(z) = - |
1
у
х
0
|
f(tz) d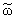 (t) (t) |
| принадлежит пространству Харди H2
в единичном шаре. При
этом
| f(z) = |
у
х
S
|
j0(z)C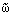 (z,z) ds(z). (z,z) ds(z). | |
Кроме того,
Отметим, что в случае, когда w(x) = nтx1 tn-1(1-t)a dt (a > -1), соответствующее пространство
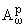 , следуя [2], будем обозначать через
Hp(a). Ввиду (6) условие (2) записывается в
виде , следуя [2], будем обозначать через
Hp(a). Ввиду (6) условие (2) записывается в
виде
| ||f||Hp(a) = |
м
н
о |
у
х
B
|
(1-|w|2)a|f(w)|p dn(w) |
ь
э
ю |
1/p
|
< +Ґ. | | Если в
теореме 3 взять
|
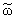 (x) = (x) = |
|
|
1
у
х
x
|
tn-1(1-t)[(a-1)/2]dt, | | то
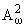 = H2(a). Поэтому из теоремы 3 вытекает = H2(a). Поэтому из теоремы 3 вытекает
Теорема 4.
Пусть функция f(z) принадлежит классу
H2(a), (a >
-1). Тогда функция
| j0(z) = |
|
|
1
у
х
0
|
f(tz)tn-1(1-t)[(a-1)/2]dt | |
принадлежит H2(B) и имеет место
интегральное представление
| f(z) = |
у
х
S
|
|
j0(z) ds(z)
(1-бz,zс)n+[(a+1)/2]
|
. | |
Теорема 4 является многомерным аналогом теоремы V из [2], при a = 0 установленной М. В. Келдышем.
Введем в рассмотрение оператор
K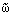 j(z)= j(z)= |
у
х
S
|
j(z)C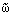 (z,z) ds(z). (z,z) ds(z). | |
Теорема 5. Функции класса
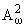 представимы в виде
представимы в виде
f(z) = K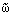 j(z), j(z), | |
где j - произвольная функция из
L2(S).
Следующая теорема, относящаяся к свойствам
оператора K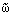 , дополняет
утверждения теорем 3 и 5. , дополняет
утверждения теорем 3 и 5.
Теорема 6. Оператор K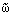 обладает следующими свойствами:
обладает следующими свойствами:
1° K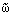 является линейным ограниченным оператором с
областью определения L2(S) и областью значений является линейным ограниченным оператором с
областью определения L2(S) и областью значений
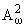 (B). (B).
2° Сужение K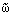 на H2(S)
является изометрией между H2(S) и на H2(S)
является изометрией между H2(S) и
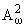 (B),
при этом обратным оператором этой изометрии является L (B),
при этом обратным оператором этой изометрии является L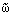 . .
3° Ядром K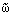 служит ортогональное дополнение к
H2(S), т. е. служит ортогональное дополнение к
H2(S), т. е.
Ker K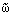
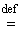 {j О L2(S): K {j О L2(S): K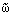 j =
0} = H^2(S), j =
0} = H^2(S), | |
где
H2^(S) Е H2(S) = L2(S).
4° ||K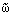 || = 1, a точнее ||K || = 1, a точнее ||K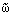 j|| j||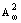 (B) Ј ||j||L2(S), где знак
равенства имеет место в том и только в том случае, если j О H2(S). (B) Ј ||j||L2(S), где знак
равенства имеет место в том и только в том случае, если j О H2(S).
5° j0
минимизирует ||j||L2(S) на
множестве всех функций j, для которых K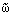 j = K j = K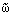 j0. Иными
словами j0. Иными
словами
| ||j0||L2(S) = |
min
j1
О H^2
|
||j0+j1||L2(S). | |
Ереванский государственный
университет
Литература 1. Джрбашян М. М.
-ДАН АрмССР. 1945. Т. 3. N I. C. 3-9.
2. Джрбашян М. М.
-Сообщ. Ин-та матем. и мех. АН АрмССР. 1948. Т.
2. C. 3-40.
3. Jerbashian
A.M. - Preprint 2002-01. December 12. 2002. Institute of
Mathematics. NAS of Armenia.
4. Джрбашян А. М., Аветисян К. Л. ДНАН Армении. 2002. T. 102. N 2. C. 105-112.
5.
W. Rudin Function theory in the Unit Ball of Cn. Springer-Verlag. N. Y. 1980. Рус. пер: У. Рудин. Теория функций в единичном шаре из Cn. M. Мир. 1984. 445 c.
| ![]() )],
)], ![]()
![]() w < Ґ для любого d О [0,1);
w < Ґ для любого d О [0,1);