МАТЕМАТИКА
УДК 517.547
А. О. Карапетян
Весовые
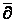 - интегральные представления в матричном круге
- интегральные представления в матричном круге
(Представлено академиком Н. У. Аракеляном 3/VII 2002 )
Пусть m,n і 1 -
произвольные натуральные числа. Обозначим через Mmn пространство всех
комплексных m×n - матриц. Для произвольной матрицы z
О Mnm через z* О Mmn
обозначается эрмитово сопряженная к z матрица. Далее,
Im(m і 1) - единичная m×m - матрица из
Mmm. Лебегова мера в Mmn вводится естественным образом:
| dmmn(z) = |
m
Х
k=1
|
|
n
Х
j=1
|
dm(zkj),
z = (zkj)1 Ј
k Ј m, 1 Ј j Ј
n. | |
Мaтричным единичным кругом называется область Rmn = {z О
Mmn : Im - z · z* положительно определена}.
При 1 Ј p < Ґ, a > -1 пространство
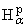 (Rmn) определяется как
множество всех голоморфных функций f(z), z О Rmn, удовлетворяющих
условию
(Rmn) определяется как
множество всех голоморфных функций f(z), z О Rmn, удовлетворяющих
условию
|
у
х
Rmn
|
|f(z)|p · [det(Im) - z · z*)]admmn(z) <
+Ґ. | |
Заметим,
что при m = 1, n і 1 Rmn есть единичный шар
Bn М Cn, а пространство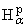 (Rmn) є
(Rmn) є
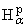 (Bn) задается условием
(Bn) задается условием
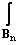 |f(z)|p · (1-|z|2)adm1n(z) < +Ґ. При m = n = 1, т.е. в случае единичного круга
|f(z)|p · (1-|z|2)adm1n(z) < +Ґ. При m = n = 1, т.е. в случае единичного круга
D
М C, эти
пространства были введены в [1,2], где была установлена формула
| f(z) = |
a+1
p
|
· |
у
х |
у
х
D
|
|
f(z)(1 - |z|2)a
(1 - z ·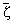 )2+a )2+a
|
dm(z),
z О D,
"f О
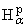 (D). (D). | |
(1) |
Это
представление нашло многочисленные применения в теории факторизации мероморфмых
функций и других вопросах комплексного анализа. Позднее аналогичные весовые
формулы начали представлять интерес и в случае различных многомерных
областей.
Так, в [3] был установлен следующий
аналог формулы (1) для функций f О
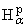 (Rmn) при a = 0:
(Rmn) при a = 0:
| f(z) = const
· |
у
хRmn |
|
f(z)dmmn(z)
[det(Im - z · z*)]m+n
|
, z О
Rmn. | |
(2) |
Позже, в случае шара Bn, было
установлено интегральное представление
| f(z) = const
· |
у
хBn |
|
f(z) · (1-|z|2)b
[1- < z, z >
)]n+1+b
|
dm1n(z),
z О Bn, | |
(3) |
для функций f О
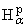 (Bn) (см. [4] при a = 0, [5,6]
при a > -1) и при условии
(Bn) (см. [4] при a = 0, [5,6]
при a > -1) и при условии
| Re b і a, если
p = 1, Re b > |
a+1
p
|
- 1, если 1 < p < Ґ. | |
(4) |
В [7,8] эти результаты были обобщены (формула (2) - в смысле
веса, а формула (3) - в смысле области). Точнее, если f О
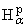 (Rmn), то
(Rmn), то
| f(z) = cmn(b) · |
у
хRmn |
|
f(z) · [det(Im - z · z*)]b
[det(Im - z · z*)]m+n+b
|
dmmn(z), z
О Rmn | |
(5) |
где b
удовлетворяет условию (4) и
| cmn(b) = |
1
pmn
|
· |
m
Х
k=1
|
G(b + k) · |
n
Х
j=1
|
G(b + j) | |
. | |
Постепенно начало выясняться, что подобные интегральные представле -ния
являются полезным инструментом в вопросах весовых решений
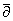 - уравнения. В этой связи
возникла необходимость установления аналогов вышеприведенных формул уже для
гладких (скажем, класса C1), а не только голоморфных функций. В [9]
для функций f О C1
- уравнения. В этой связи
возникла необходимость установления аналогов вышеприведенных формул уже для
гладких (скажем, класса C1), а не только голоморфных функций. В [9]
для функций f О C1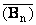 была установлена
следующая формула (Reb > -1):
была установлена
следующая формула (Reb > -1):
| f(z) = c1n(β) · |
у
хBn |
|
f(z) · (1 - |z|2)b
1 - < z, z >
)]n+1+b
|
dm1n(z) - c1n(b) · |
у
хBn |
|
<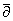 f(z),z - z > f(z),z - z >
[D(z, z)]n
|
· | |
| · (1 - < z, z > )n-1 · |
ж
з
и |
|
1 - |z|2
1 - < z, z >
|
|
ц
ч
ш |
b+1
|
· |
n-1
е
p=0
|
|
(-1)p · Cpn-1
p + b + 1
|
· | |
| · |
й
к
л |
|
(1 - |z|2)(1 - |z|2)
|1 - < z, z > |2
|
|
щ
ъ
ы |
p
|
dm1n(z),
z О Bn, | |
(6) |
где
| D(z, z) = |1 - < z, z > |2 - (1 - |z|2)(1 - |z|2). | |
В настоящей заметке приводится аналог формулы (6) для области
Rmn и, тем самым, одновременно обобщается (5) на случай гладких
функций.
Прежде чем сформулировать основной результат,
введем некоторые обозначения.
При z О
Rmn
| jz(z) = |
Ц
|
Im - zz*
|
· (Im - zz*)-1 · (z - z) · |
Ц
|
In - z*z
|
-1
|
, z
О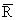 mn mn |
, | |
обозначает
дробно-рациональный автоморфизм области Rmn.
Для произвольной матрицы A О Mmn
||A|| обозначает "матричную норму",
т.е. ||A||2 есть максимальное
собственное значение матрицы A · A*.
Теорема. Пусть m,n і 1 и Re b
> -[1/m], тогда каждая функция f О C1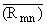 допускает представление вида
допускает представление вида
| f(z) = cmn(b) · |
у
х
Rmn
|
|
f(z) · [det(Im - zz*)]b
[det(Im - zz*)]m+n+b
|
dmmn(z) - | |
| -cmn(b) · |
у
х
Rmn
|
<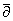 f(z),(Im - zz*)(Im - zz*)-1(z - z) > ·F(z,z)dmmn(z), z О
Rmn, f(z),(Im - zz*)(Im - zz*)-1(z - z) > ·F(z,z)dmmn(z), z О
Rmn, | |
(7) |
где
| F(z,z) = |
й
к
л |
|
det(Im - zz*)
det(Im - zz*)
|
|
щ
ъ
ы |
b
|
· |
1
[det(Im - zz*)]m+n
|
· | |
| · |
1/||jz(z)||2
у
х
1
|
tmn-1 · |
й
к
л |
det(Im - t · jz(z) · jz(z))* |
щ
ъ
ы |
b
|
dt, z №
z, z, z О
Rmn. | |
При этом справедлива оценка вида
| |F(z, z)| Ј const · ||z - z||-2mn | |
равномерно по z О Rmn, z О K М М Rmn
Институт математики НАН РА
Литература 1. Джрбашян М. М.
-ДАН АрмССР. 1945. Т. 3. N I. C. 3-9.
2. Джрбашян
М. М. - Сообщ. Ин-та матем. и мех. АН АрмССР. 1948. Вып. 2. С.
3-40.
3. Хуа Ло-кен. Гармонический анализ функций
многих комплексных переменных в классических областях. М. ИЛ. 1959.
4. Forelli F., Rudin W. - Ind. Univ. Math. J. 1974. V. 24.
N6. P. 593-602.
5. Джрбашян М. М. - Изв. АН
АрмССР. Математика. 1988. Т. 23. N 6. С. 517-545.
6. Dzhrbashian M. M. - Математически Вестник. 1987. V. 39.
P. 263-282.
7. Джрбашян М. М., Карапетян А. О.- Изв. АН АрмССР. Математика. 1989. Т.24. N6. С. 523-546.
8. Джрбашян М. М., Карапетян А. О.- ДАН СССР. 1990. Т. 312. N
1. C. 24-27.
9. Charpentier Ph. - Ann. Inst.
Fourier. 1980. V. 30. N4. P. 121.-154.
![]() - интегральные представления в матричном круге
- интегральные представления в матричном круге ![]() - интегральные представления в матричном круге
- интегральные представления в матричном круге ![]() (Rmn) определяется как
множество всех голоморфных функций f(z), z О Rmn, удовлетворяющих
условию
(Rmn) определяется как
множество всех голоморфных функций f(z), z О Rmn, удовлетворяющих
условию ![]() (Rmn) є
(Rmn) є
![]() (Bn) задается условием
(Bn) задается условием
![]() |f(z)|p · (1-|z|2)adm1n(z) < +Ґ. При m = n = 1, т.е. в случае единичного круга
|f(z)|p · (1-|z|2)adm1n(z) < +Ґ. При m = n = 1, т.е. в случае единичного круга ![]() )2+a
)2+a![]() (D).
(D).![]() (Rmn) при a = 0:
(Rmn) при a = 0: ![]() (Bn) (см. [4] при a = 0, [5,6]
при a > -1) и при условии
(Bn) (см. [4] при a = 0, [5,6]
при a > -1) и при условии
![]() (Rmn), то
(Rmn), то ![]() - уравнения. В этой связи
возникла необходимость установления аналогов вышеприведенных формул уже для
гладких (скажем, класса C1), а не только голоморфных функций. В [9]
для функций f О C1
- уравнения. В этой связи
возникла необходимость установления аналогов вышеприведенных формул уже для
гладких (скажем, класса C1), а не только голоморфных функций. В [9]
для функций f О C1![]() была установлена
следующая формула (Reb > -1):
была установлена
следующая формула (Reb > -1): ![]() f(z),z - z >
f(z),z - z >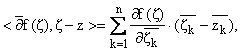
![]() mn
mn ![]() допускает представление вида
допускает представление вида ![]() f(z),(Im - zz*)(Im - zz*)-1(z - z) > ·F(z,z)dmmn(z), z О
Rmn,
f(z),(Im - zz*)(Im - zz*)-1(z - z) > ·F(z,z)dmmn(z), z О
Rmn,