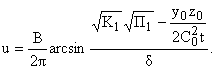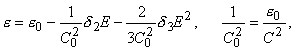ФИЗИКА
УДК 539.1
Член-корреспондент НАН РА А.Г.Багдоев, Ю.С.Сафарян,
Г.А.Мартиросян
Нелинейная нестационарная пространственная задача дифракции
электромагнитной волны при ее произвольной поляризации
(Представлено 22/VII 2002)
Рассматривается задача о прохождении плоской
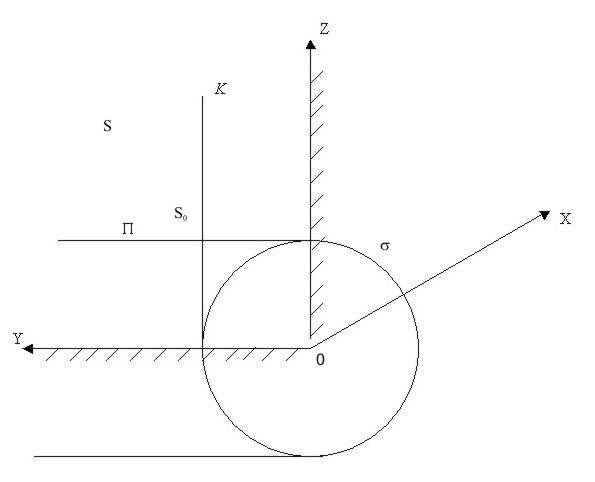
электромагнитной волны около непрозрачного экрана в форме угла раствора [(3p)/2] в нелинейной среде. Ставится задача определения
линейного и нелинейного решения в окрестности линий касания плоской отраженной
волны S с цилиндрическими волнами K и P, произведенными
краями экрана (рисунок), а затем и решений в полной окрестности точки B касания
указанных волн со сферической волной s, произведенной
вершиной O. Уравнения Максвелла имеют вид
в
последнем уравнении нелинейностью пренебрегаем, и для малых
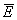 можно считать
можно считать
|
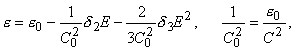
|
(1) |
C - скорость света вне нелинейной
среды, E2 = Ey2 + Ez2.
Предположим, что падающая волна линейно
поляризована, оси y,z направлены по краям экрана, ось x перпендикулярна к ним и
к плоскости падающей и плоской отраженной волны, электрическое поле на начальной
волне имеет компоненты Ey0 = A, Ez0 = B.
Уравнения Максвелла дают
|
¶2Ey,z
¶x2
|
+ |
¶2Ey,z
¶y2
|
+ |
¶2Ey,z
¶z2
|
= |
1
C02
|
|
¶2
¶t2
|
|
м
н
о |
ж
з
и |
1 - d2E - |
2
3
|
d3E2 |
ц
ч
ш |
Ey,z |
ь
э
ю |
. | |
(2) |
В дальнейшем будет рассмотрена
кубическая среда d2 = 0. Линейная задача
соответствует уравнению (2) в форме
|
¶2u
¶t2
|
= C02 |
ж
з
и |
¶2u
¶x2
|
+ |
¶2u
¶y2
|
+ |
¶2u
¶z2
|
ц
ч
ш |
,
u = Ey,z. | |
(3) |
Таким образом, линейная задача
распадается на задачи определения: u = Ey при начальном условии в
плоскости y,z вне экрана Ey = A; u = Ez при условии
Ez = B. Ищем решение в указанной выше окрестности точки B касания
цилиндрических, плоских и сферических волн. При решении задачи о начальных
условиях, заданных позади падающей волны, для уравнения (3) следует записать [1]
| u = tMc0t(F1) + |
¶tMc0t(F0)
¶t
|
, | |
(4) |
где Mc0t(F) есть поделенный на 4pC02t2 интеграл от F, взятый по поверхности сферы радиуса C0t с
центром в точке M(x0,y0,z0), в которой
определяется решение, F0,F1 есть значения u, [(¶u)/(¶t)] позади начальной волны
S0. При определении решения в точке M, находящейся вблизи волны S, а
также вблизи точки B, следует интегрировать по поверхности указанной сферы,
отсекаемой S0. Уравнение сферы имеет следующий вид:
| (x - x0)2 + (y - y0)2 + (z - z0)2 = C02t2; | |
для
малых x и C0t - x0 = C0d
| x = - C0d + |
(y - y0)2 + (z - z0)2
2C0t
|
. | |
Уравнение S0 относительно сферы имеет вид
| zў = 0, zў = C0d - |
(y - y0)2
2C0t
|
- |
(z - z0)2
2C0t
|
, | |
(5) |
где zў = -x, x есть координата точки
интегирования позади начальной волны.
Начальные условия, например, для
Ez, имeют вид
|
| u(x,y,z,0) = F0 = Bs(zў)s(y)s(z), | |
|
¶u(x,y,z,0)
¶t
|
= F1 = Bd(zў)s(y)s(z), | | |
| |
(6) |
где B = const,
s(zў) есть единичная функция,
d(z) есть дельта-функция и выбор условий (6) обусловлен
теорией Кирхгоффа [2] о необходимости интегрировать по освещенной части
начальной волны S0 и плоскости x = 0 вне экрана. Таким образом, на
область интегрирования накладываются следующие условия:
Из (4), (6) имеем
| u = |
1
2pC0 t
|
|
у
х |
|
у
х |
Bd(zў)dydz, | |
(8) |
где область интегрирования дается в
(7).
Введя переменные x,h, причем,
|
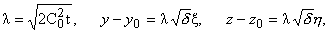
|
(9) |
для области интегрирования в (8)
можно записать
|
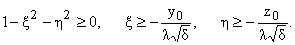
|
(10) |
Область интегрирования меняется в зависимости от расположения точки
(x0,y0,z0)
|
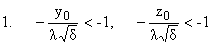
|
(11) |
Обозначая d0 = t - tg,
где d0 = 0 есть
уравнение волны s, причем
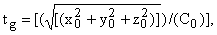 и учитывая, что при t = tg в (5) y = 0, z = 0, zў = c0d0, можно
получить уравнение S относительно s
и учитывая, что при t = tg в (5) y = 0, z = 0, zў = c0d0, можно
получить уравнение S относительно s
| d = d0 + |
1
2C02t
|
y02 + |
1
2C02t
|
z02,
d = 0 | |
(12) |
Кроме того, если ввести переменные
величины
| K1 = d0 + |
1
l2
|
z02,
P1 = d0 + |
1
l2
|
z02, | |
(13) |
условие (11) примет вид
| y0 >
0, z0 > 0, K1 <
0, P1 <
0. | |
(14) |
Здесь K1 = 0 есть
уравнение цилиндра K (рисунок), касающегося сферы s
вдоль линии z0 = 0.
Подобным же образом P1 = 0
представляет уравнение цилиндрической поверхности P,
касающейся сферы s вдоль линии y0 = 0.
Решение (11) в указанной области согласно (8)
имеет вид
| u = |
B
p
|
|
у
х |
|
у
х |
d(1 - x2 - h2)dxdh, | |
(15) |
причем интегрирование ведется по
области (10), которой в данном случае будет весь круг x2 + h2 Ј 1. Можно получить, что в этой области решение постоянно и
по (15) имеет вид u = B.
Таким образом, область (11) есть область
постоянного решения и ограничена плоскостью S, поверхностями K и P.
|
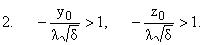
|
(16) |
Тогда y0 < 0,
z0 < 0, K1 < 0, P1 < 0, причем из (10) и (15) следует u = 0.
Указанная область находится вне сферы s и вне цилиндров
K и P.
|
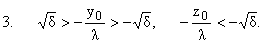
|
(17) |
Oтсюда следует z0 >
0, P1 < 0, K1 > 0.
Область интегрирования дается (10), причем из
(16) получится
|
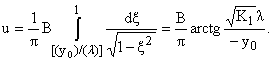
|
(18) |
Полученное решение верно внутри
цилиндра K и вне поверхности P (a также сферы d0 = 0).
|

|
(19) |
Отсюда следует y0 >
0, K1 < 0, P1 > 0. Область
интегрирования дается (10), из (15) получится
|
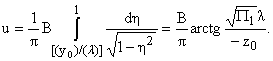
|
(20) |
Полученное решение верно внутри
цилиндра P и вне цилиндра K и сферы s. Следует отметить, что в (18), (20) при y0 <
0 и z0 < 0 решение на K и P
соответственно обращается в нуль, тогда как при y0 > 0 и
z0 > 0 согласно соотношению arctg(-x) = p-arctgx решение на K и P равно B, что
соответствует части поверхностей K и P, граничащей с
областью (11).
|

|
(21) |
Область интегрирования дается (10),
причем из (15) получится
|
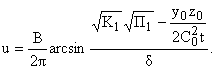
|
(22) |
Точка
(x0,y0,z0) находится вблизи участка сферы s.
Рассмотрим задачу определения нелинейного
решения в области 3 вблизи цилиндрической волны K, где решение двумерное и
определяется переменными K1,y0. В нелинейной задаче
функции Ey и Ez связаны, причем линейные решения для
Ez даются (8)-(21), а для Ey теми же соотношениями с
заменой B на A. Аналогично можно получить решение в области 4 вблизи
цилиндрической волны P, определяемое P1,z0. Эти решения соответствуют
упрощенным нелинейным уравнениям коротких волн [3]
|
1
3
|
d3 |
¶
¶dў
|
(E2Ez,y) - dў |
¶Ez,y
¶dў
|
+ |
1
2
|
Ez,y + |
1
2
|
|
¶Vy,z
¶y
|
= 0, |
¶Vy,z
¶dў
|
= |
¶Ez,y
¶y
|
, | |
(23) |
где dў = [(K1)/t], [(y0)/(C0t)] = y и функции Vy,z введены по (23). Решение нелинейной задачи, как и в
случае одной функции u [3], находится сращиванием с линейным решением (18),
причем m = [(Ez)/B], mў = [(Ey)/A] и, как
показывает (18), mў = m, Vy = [A/B] Vz, и (23) дает
| Vy = |
ж
з
и |
|
1
p
|
Btgpm - Bm |
ц
ч
ш |
y, dў = - |
1
2
|
my2tg2p + F(m). | |
(24) |
Уравнения (23) примут вид
|
1
3
|
(B2 + A2)d3 |
¶
¶dў
|
m3 - dў |
¶m
¶dў
|
+ |
1
2
|
m + |
1
2B
|
|
¶Vy
¶y
|
= 0, |
1
B
|
|
¶Vy
¶dў
|
= |
¶m
¶y
|
. | |
(25) |
Подставляя (24) в (25), где
поменены ролями dў и m, получим
| F(m) = -(B2 + A2)d3m2 - (B2 + A2)d3 |
1
p
|
msin2pm + 2(B2 + A2)d3sin2pmlnsinpm | |
(26) |
Решение (24) и (26) удовлетворяет
уравнениям (25) и условию сращивания с линейным решением (18), для которого F
следует отбросить. Таким же образом находится решение нелинейной задачи вблизи
волны P. Найдем нелинейное решение вблизи волны s. Уравнения движения вблизи точки B имеют вид [3]
|
|
¶u
¶t
|
+ |
1
2
|
C0 |
¶Vy
¶y0
|
+ |
1
2
|
C0 |
¶Vz
¶z0
|
+ |
1
3
|
d3 u2 |
¶u
¶t0
|
+ |
u
t
|
= 0, | |
|
¶u
¶y0
|
= |
¶Vy
C0¶t0
|
, |
¶u
¶z0
|
= |
¶Vz
C0¶t0
|
. | | |
| |
(27) |
Из последних двух уравнений,
обозначая [(z0)/(C0t)] = z, [(t0)/t] = -t и подставляя u из (22), можно получить Vy,
Vz в линейном случае, выражая их через m и
считая, что эти выражения верны и в нелинейном случае. Можно, подставляя их в
первое уравнение, получить решение в виде
|
| t0ў2cos2pm =
(y2 + z2)sin22pm + 2yzsin2pm, | |
| t =
t0ў - d3(A2 + B2)m2 + 2d3sin2pm(A2 + B2) |
m
у
х
1
|
|
mdm
sin2pm
|
. | | |
| |
(28) |
Институт механики НАН РА
Горисский филиал ГИУА
Литература
1. Фридлендер Ф. Звуковые импульсы. М. ИЛ. 1962. 232 с.
2. Виноградова М.Б., Руденко
О.В., Сухорунов А.П. Теория волн. М. Наука. 1979. 384
с.
3. Багдоев А.Г., Гургенян А.А.
- Изв. АН АрмССР. 1968. Т.21. N1. С. 39-56.
![]() и учитывая, что при t = tg в (5) y = 0, z = 0, zў = c0d0, можно
получить уравнение S относительно s
и учитывая, что при t = tg в (5) y = 0, z = 0, zў = c0d0, можно
получить уравнение S относительно s 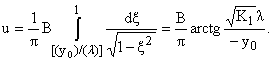
![]()
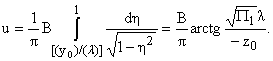
![]()