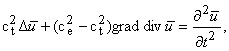ТЕОРИЯ УПРУГОСТИ

УДК 539.3

М.В. Белубекян

О полноте решений типа Ламе для плоских задач

(Представлено академиком С.А. Амбарцумяном 17/IX 2002)

   Рассматривается вопрос полноты решений типа Ламе для двухслойной пластинки на основе гипотезы Кирхгофа и для изгибных колебаний однослойной пластинки с учетом поперечных сдвигов.
   1. Уравнения движения теории упругости имеют вид

(1.1)

где - вектор упругих перемещений, ce,ct - скорости распространения объемных продольных и поперечных волн соответственно.
   Введением преобразования

(1.2)
Ламе (1839) привел решение уравнения (1.1) к решению следующих уравнений:

(1.3)

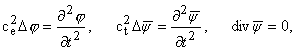
То, что решения Ламе (или функции Ламе) являются решениями уравнения (1.1), следует непосредственно из процедуры получения уравнений (1.3).
   Утверждение, что все решения уравнения (1.1) даются уравнениями (1.3), требует доказательства. Теорема полноты впервые была сформулирована Клебшем (1863), однако его доказательство считается неубедительным [1]. Строгое доказательство полноты дано Сомиляни (1892) и Дюгемом (1898).
   Доказательства Сомиляни и Дюгема приводятся в монографиях [1,2], соответственно. Обобщение доказательства на случай наличия массовых сил получено Стернбергом (1960) [1].
   Очевидно, что теорема полноты Клебша имеет место и в частном случае задачи плоской деформации. Так как нас интересуют плоские задачи теории упругости (обобщенное плоское напряженное состояние, теория пластин с учетом поперечных сдвигов), ниже приводится решение Ламе и доказательство полноты для задачи плоской деформации.
   Принимается, что в прямоугольной декартовой системе координат (x,y,z) перемещения не зависят от координаты z. Тогда для компонент перемещений u,v в плоскости (x,0,y) уравнения движения имеют вид

ct2Du + (ce2 - ct2)
x
 ж
з
и 		u
x
 + v
y
 ц
ч
ш 		= 2u
t2
 ,
ct2Dv + (ce2 - ct2)
y
 ж
з
и 		u
x
 + v
y
 ц
ч
ш 		= 2v
t2
 .
(1.4)
Здесь и в дальнейшем D - двумерный оператор Лапласа.
   Для задачи плоской деформации преобразование (1.2) имеет вид
u = j
x
 + y
y
 ,   v = j
y
 - y
x
 .
 (1.5)
Подстановка (1.5) в (1.4) приводит к следующей системе уравнений:
x
 ж
з
и 		ce2Dj - 2j
t2
 ц
ч
ш 		+
y
 ж
з
и 		ct2Dy - 2y
t2
 ц
ч
ш 		= 0,
y
 ж
з
и 		ce2Dj - 2j
t2
 ц
ч
ш 		-
x
 ж
з
и 		ct2Dy - 2y
t2
 ц
ч
ш 		= 0.
(1.6)
Из (1.6) следует, что решения уравнений
ce2Dj = 2j
t2
 ,  ct2Dy = 2y
t2
 ,
 (1.7)
с учетом (1.5), будут удовлетворять уравнениям (1.4).
   Для доказательства полноты, следуя Сомиляни, систему уравнений (1.4) преобразуем к виду
2u
t2
 = ce2
x
 ж
з
и 		u
x
 + v
y
 ц
ч
ш 		+ ct2
y
 ж
з
и 		u
y
 - v
x
 ц
ч
ш 		,
2v
t2
 = ce2
y
 ж
з
и 		u
x
 + v
y
 ц
ч
ш 		- ct2
x
 ж
з
и 		u
y
 - v
x
 ц
ч
ш 		.
(1.8.)
Уравнения (1.8) интегрируются по t при начальных условиях
u = 0,   u
t
 = 0,  v = 0,   v
t
 = 0,
 (1.9)
что дает
u = ce2
x
 t
у
х
0 
 t
у
х
0 
 ж
з
и 		u
x
 + v
y
 ц
ч
ш 		dhdt + ct2
y
 t
у
х
0 
 t
у
х
0 
 ж
з
и 		u
y
 - v
x
 ц
ч
ш 		dhdt,
v = ce2
y
 t
у
х
0 
 t
у
х
0 
 ж
з
и 		u
x
 + v
y
 ц
ч
ш 		dhdt - ct2
x
 t
у
х
0 
 t
у
х
0 
 ж
з
и 		u
y
 - v
x
 ц
ч
ш 		dhdt.
(1.10)
Вводятся обозначения
j = ce2 t
у
х
0 
 t
у
х
0 
 ж
з
и 		u
x
 + v
y
 ц
ч
ш 		dhdt,  y = ct2 t
у
х
0 
 t
у
х
0 
 ж
з
и 		u
y
 - v
x
 ц
ч
ш 		dhdt.
 (1.11)
Выражения (1.11) дважды дифференцируются по t
2 j
t2
 = ce2 ж
з
и 		u
x
 + v
y
 ц
ч
ш 		,   2y
t2
 = ct2 ж
з
и 		u
y
 - v
x
 ц
ч
ш 		.
 (1.12)
Так как согласно (1.5)
u
x
 + v
y
 = Dj,   u
y
 - v
x
 = Dy,
 (1.13)

то отсюда следует, что решение системы (1.4) удовлетворяет уравнениям (1.7). Согласно [1] приведенное здесь доказательство полноты по Сомиляни легко обобщается на случай произвольных начальных условий и наличия объемных сил.
   2. Пусть двухслойная пластинка в прямоугольной декартовой системе координат занимает область 0 Ј x Ј a, 0 Ј y Ј b, -h2 Ј z Ј h1. В последующем индекс 1 относится к слою 0 < z Ј h1, а индекс 2 - к слою -h2 Ј z1 < 0. Принимается гипотеза Кирхгофа для пакета в целом. При приведенных допущениях уравнения колебаний пластинки имеют вид [3]

Du + q
x
 ж
з
и 		u
x
 + v
y
 ц
ч
ш 		- k1 - k2
q
x
 Dw = m1 + m2
q
 2u
t2
 ,
Dv + q
y
 ж
з
и 		u
x
 + v
y
 ц
ч
ш 		- k1 - k2
q
y
 Dw = m1 + m2
q
 2v
t2
 ,
(2.1)

(D1 + D2)D2w + (m1 + m2) 2w
t2
 - (k1 - k2)D ж
з
и 		u
x
 + v
y
 ц
ч
ш 		= 0.
 (2.2)
Здесь u,v,w - перемещения плоскости раздела слоев (z = 0)
mi = rihi,  Ci = Eihi/(1-n2i),  ki = Eihi2/2(1-ni2),
Di = Eihi3/(1-ni2),  i = 1,2,
q = 2-1[(1-n1)c1 + (1-n2)c2],  q = 2-1q-1[(1+n1)c1+(1+n2)c2],
(2.3)
Ei - модули Юнга, ni - коэффициенты Пуассона, ri - плотности масс соответствующих слоев.
   Уравнения (2.1) аналогичны уравнениям задачи плоской деформации (1.4). Члены с Dw можно рассматривать как компоненты объемной силы. Преобразование
u = j
x
 + y
y
 + k1-k2
c1+c2
 w
x
 ,    v = j
y
 - y
x
 + k1-k2
c1+c2
 w
y
(2.4)
приводит уравнение (2.1) к виду, аналогичному (1.6), откуда следуют следующие уравнения:
cd2Dj = 2j
t2
 ,    cr2Dy = 2y
t2
 ,
 (2.5)
где
cd2 = c1 + c2
m1 + m2
 ,    cr2 = q
m1 + m2
 .
 (2.6)
С другой стороны, система (2.1) преобразуется к виду
2u
t2
 = cd2
x
 ж
з
и 		u
x
 + v
y
 ц
ч
ш 		- k1-k2
m1+m2
x
 Dw + cr2
y
 ж
з
и 		u
y
 - v
x
 ц
ч
ш 		,
2v
t2
 = cd2
y
 ж
з
и 		u
x
 + v
y
 ц
ч
ш 		- k1-k2
m1+m2
y
 Dw - cr2
x
 ж
з
и 		u
y
 - v
x
 ц
ч
ш 		.
(2.7)

Отсюда уже ясно, что процедура доказательства Сомиляни проходит и для рассматриваемых здесь уравнений. Систему уравнений (2.7) необходимо дважды интегрировать по t при нулевых начальных условиях и затем ввести обозначения

j = t
у
х
0 
 t
у
х
0 
 й
к
л 		c2d ж
з
и 		u
x
 + v
y
 ц
ч
ш 		- k1-k2
m1+m2
 Dw щ
ъ
ы 		dhdt,  y = ct2 t
у
х
0 
 t
у
х
0 
 ж
з
и 		u
y
 - v
x
 ц
ч
ш 		dhdt.
 (2.8)
Продифференцировав выражения (2.8) дважды по t и учитывая, что
u
x
 + v
y
 = Dj + k1-k2
c1+c2
 Dw,    u
y
 - v
x
 = Dy,
 (2.9)
придем к уравнениям (2.5), чем и завершается доказательство полноты.
   3. Уравнения изгибных колебаний пластинки толщиной 2h на основе теории С.А.Амбарцумяна записываются в виде [4]
8h2
15
 й
к
л 		Dj1 + q
x
 ж
з
и 		j1
x
 + j2
y
 ц
ч
ш 		щ
ъ
ы 		- 4h
3
 j1 - D
x
 Dw = 2rh3
3
 2
t2
 ж
з
и 		w
x
 - 4
5G
 j1 ц
ч
ш 		,
8h3
15
 й
к
л 		Dj2 + q
y
 ж
з
и 		j1
x
 + j2
y
 ц
ч
ш 		щ
ъ
ы 		- 4h
3
 j2 - D
y
 Dw = 2rh3
3
 2
t2
 ж
з
и 		w
y
 - 4
5G
 j2 ц
ч
ш 		,
j1
x
 + j2
y
 = 3r
2
 2w
t2
 ,   q = 1 + n
1 - n
 .
(3.1)
Преобразование
j1 = f
x
 + y
y
 ,    j2 = f
y
 - y
x
(3.2)
приводит первые два уравнения системы (3.1) к системе уравнений, аналогичных системе (1.6), откуда следуют следующие уравнения [4,5]:
-DDw + 2rh3
3
 2w
t2
 + 8ch3
3(1-n)
 Df - 4h
3
 f- 4crh3
3G
 2f
t2
 = 0,
Dy - 1
ch2
 y - r
G
 2y
t2
 = 0,    c = 2
5
 .
(3.3)
Для доказательства полноты первые два уравнения системы (3.1) преобразуются к виду
2j1
t2
 + a2j1 = f(t),    2j2
t2
 + a2j2 = g(t)
 (3.4)
где
f(t) = g-1 м
н
о
x
 й
к
л 		16h3
15(1-v)
 ж
з
и 		j1
x
 + j2
y
 ц
ч
ш 		- DDw + 2rh3
3
 2w
t2
 щ
ъ
ы 		+ 16h3
15(1-v)
y
 ж
з
и 		j1
y
 - j2
x
 ц
ч
ш 		ь
э
ю
g(t) = g-1 м
н
о
y
 й
к
л 		16h3
15(1-v)
 ж
з
и 		j1
x
 + j2
y
 ц
ч
ш 		- DDw + 2rh3
3
 2w
t2
 щ
ъ
ы 		- 16h3
15(1-v)
x
 ж
з
и 		j1
y
 - j2
x
 ц
ч
ш 		ь
э
ю
a2 = 5G
2rh2
 ,   g = 8rh3
15G
(3.5)
Уравнения (3.4) имеют следующие решения, удовлетворяющие нулевым начальным условиям:
j1 = 1
a
 t
у
х
0 
 f(t)sina(t-t)dt,   j2 = 1
a
 t
у
х
0 
 g(t)sina(t-t)dt.
 (3.6)
С учетом (3.5) в (3.6) принимаются следующие обозначения:
F = 1
ag
 t
у
х
0 
 й
к
л 		16h3
15(1-v)
 ж
з
и 		j1
x
 + j2
y
 ц
ч
ш 		-DDw + 2rh3
3
 2w
t2
 щ
ъ
ы 		sina(t-t)dt.
 (3.7)
Дифференцированием выражений (3.7) дважды по t, использованием (3.6) и равенств
j1
x
 + j2
y
 = DF,    j1
y
 - j2
x
 = DY
 (3.8)
показывается, что функции F и Y и (3.7) удовлетворяют уравнениям (3.3), что и доказывает полноту.
   4. Уравнения изгибных колебаний пластинки с учетом поперечных сдвигов типа Рейснера имеют вид [6]
D й
к
л 		Dq1 + q
x
 ж
з
и 		q1
x
 + q2
y
 ц
ч
ш 		щ
ъ
ы 		+ 4Gh
1-v
 ж
з
и 		w
x
 -q1 ц
ч
ш 		= 4rh3
3(1-v)
 2q1
t2
 ,
D й
к
л 		Dq2 + q
y
 ж
з
и 		q1
x
 + q2
y
 ц
ч
ш 		щ
ъ
ы 		+ 4Gh
1-v
 ж
з
и 		w
x
 -q1 ц
ч
ш 		= 4rh3
3(1-v)
 2q2
t2
 ,
2Gh ж
з
и 		Dw - q1
x
 - q2
y
 ц
ч
ш 		= 2rh 2w
t2
 .
(4.1)
При помощи преобразования [5]
q1 = w
x
 - 2
3G
 ж
з
и 		F
x
 + Y
y
 ц
ч
ш 		,   q2 = w
y
 - 2
3G
 ж
з
и 		F
x
 - Y
y
 ц
ч
ш
(4.2)
первые два уравнения системы (4.1) приводятся к уравнениям (3.3) с c = 1/3. После чего доказательство полноты аналогично доказательству, приведенному в пункте 3.

     Институт механики НАН РА


Литература

     1. Miklowitz J.  The theory of elastic waves and waveguides. North-Holland. 1984. 618 p.
     2. Новацкий В.  Теория упругости. М. Мир. 1975. 872 с.
     3. Амбарцумян С.А., Белубекян М.В.  - Проблемы прочности и пластичности. Межвуз. сб. Вып 61. Н.-Новгород. 2000. С.26-30.
     4. Белубекян В.М. Белубекян М.В.  - Изв. НАН Армении. Механика. 1999. Т.52. N2. С. 11-21.
     5. Белубекян М.В.  В сб.: Проблемы механики тонких деформируемых тел. Ереван. Изд. НАН Армении. 2002. С. 67-88.
     6. Васильев В.В.  - Изв. РАН. МТТ. 1998. N3. С. 46-58.