УДК 510.52

   В различных областях прикладной математики на протяжении последних 30 лет большое внимание уделяется изучению так называемых NP-полных задач. В основополагающих работах [1,2] приведены определение и доказательство существования таких задач и отмечена их тесная взаимосвязь друг с другом. Список NP-полных задач быстро растет и в настоящее время содержит, согласно [3], около десяти тысяч задач. Первые попытки их систематизации и классификации были сделаны в [4].
   Исторически первой NP-полной задачей является задача из математической логики, известная под названием "ВЫПОЛНИМОСТЬ" [1]. Важный частный случай этой задачи, известный под названием "3-ВЫПОЛНИМОСТЬ", также представляет собой NP-полную задачу [1] и часто употребляется для доказательства NP-полноты задач из теории графов и комбинаторного анализа [2,4,5].
   Настоящее исследование посвящено более подробному анализу задачи "3-ВЫПОЛНИМОСТЬ". В работе сформулирована задача "СВЯЗНАЯ 3-ВЫПОЛНИМОСТЬ", являющаяся интересным частным случаем задачи "3-ВЫПОЛНИМОСТЬ", и доказана ее NP-полнота. Предложен соответствующий полиномиальный алгоритм сведения задачи "3-ВЫПОЛНИМОСТЬ" к задаче "СВЯЗНАЯ 3-ВЫПОЛНИМОСТЬ". Не определяемые понятия можно найти в [1,2,5-7].
   Пусть  X={ x₁,x₂,ј,x_n}  есть  множество  булевых  переменных,  D={ D₁,D₂,ј,D_r} - множество дизъюнкций, составленных из литералов переменных множества X, t(D_i) обозначает множество индексов переменных, входящих в дизъюнкцию D_i, i = 1,2,ј, r, и K(x₁,x₂,ј,x_n) = D₁&D₂&ј&D_r - конъюнктивная нормальная форма.
   Определение. Графом G(K(x₁,x₂,ј,x_n)) конъюнктивной нормальной формы   K(x₁,x₂,ј,x_n) называется   граф,   для   которого   множества V(G(K(x₁,x₂,ј,x_n))) и E(G(K(x₁,x₂,ј,x_n))) вершин и ребер, соответственно, определяются следующим образом:

V(G(K(x1,x2,ј,xn))) є 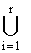V(Di), где при i = 1,2,ј,r

V(Di) = { vj(i)|1 Ј j Ј n, j О t(Di)};

E(G(K(x1,x2,ј,xn))) є E1(G(K(x1,x2,ј,xn)))ИE2(G(K(x1,x2,ј,xn))),

где E1(G(K(x1,x2,ј,xn))) =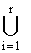E1i(G(K(x1,x2,ј,xn))),  и для i = 1,2,ј,r

E1i(G(K(x1,x2,ј,xn))) = {(u,w)|{ u,w} Н V(Di), u № w},

E2(G(K(x1,x2,ј,xn))) = 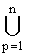E2p(G(K(x1,x2,ј,xn))),  и для p = 1,2,ј,n

E2p(G(K(x1,x2,ј,xn))) = {(vp(s), vp(t))|1 Ј s Ј r, 1 Ј t Ј r, s № t, p О t(Ds)Зt(Dt)}.

   Задача: СВЯЗНАЯ 3-ВЫПОЛНИМОСТЬ.
   Условие: Пусть X есть множество булевых переменных, и K(x₁,x₂,ј,x_n) = D₁&D₂&ј&D_r есть конъюнктивная нормальная форма, составленная из дизъюнкций, каждая из которых содержит 3 литерала переменных множества X, и граф G(K(x₁,x₂,ј,x_n)) связный.
   Вопрос: Существует  ли  такая  последовательность  (a₁,a₂,ј,a_n)  с a_i О {0,1} для i = 1,2,ј,n, для которой K(a₁,a₂,ј,a_n) = 1?
   Теорема. Задача "СВЯЗНАЯ 3-ВЫПОЛНИМОСТЬ" NP-полна.
   Доказательство. Принадлежность задачи "СВЯЗНАЯ 3-ВЫПОЛНИМОСТЬ" к классу NP следует из того, что эта задача есть частный случай задачи "3-ВЫПОЛНИМОСТЬ", NP-полнота которой была установлена в [1]. Опишем полиномиальный алгоритм, сводящий задачу "3-ВЫПОЛНИМОСТЬ" к задаче "СВЯЗНАЯ 3-ВЫПОЛНИМОСТЬ".
   Пусть X(3-ВЫП.) = { x₁,x₂,ј,x_n} и D(3-ВЫП.) = { D₁,D₂,ј,D_r} есть, соответственно, множества переменных и дизъюнкций для индивидуальной задачи Iў из "3-ВЫПОЛНИМОСТИ".
   Положим:

X(СВЯЗНАЯ 3-ВЫП.) є X(3-ВЫП.)ИZ,  где Z = {zn+1,zn+2,ј,zn+r,zn+r+1 }

есть множество булевых переменных, причем ZЗX(3-ВЫП.)=Ж;

D(СВЯЗНАЯ 3-ВЫП.) є 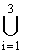D(i)(СВЯЗНАЯ 3-ВЫП.), где при i = 1,2,3

D⁽ⁱ⁾(СВЯЗНАЯ 3-ВЫП.) = { D⁽ⁱ⁾₁,D⁽ⁱ⁾₂,ј,D⁽ⁱ⁾_r}, а дизъюнкции D⁽¹⁾_j, D⁽²⁾_j, D⁽³⁾_j строятся по дизъюнкции D_j при j = 1,2,ј, r следующим образом:
если D_j = a Ъ b Ъ c, где каждое из a,b,c есть литерал переменной множества X(3-ВЫП.), то