А.О.Карапетян
Весовые
![]() -интегральные представления C1-функций в Cn
-интегральные представления C1-функций в Cn
(Представлено академиком Н.У. Аракеляном 3/VII 2002)
УДК 517.547
А.О.Карапетян
Весовые
![]() -интегральные представления C1-функций в Cn
-интегральные представления C1-функций в Cn
(Представлено академиком Н.У. Аракеляном 3/VII 2002)
Пусть n і 1, 1 <
p < +Ґ, и 0 < r, s < +Ґ, g > -2n. Определим
Lpr,s,g(Cn) как пространство
всех измеримых комплекснозначных функций f(z), z О
Cn, удовлетворяющих условию
суть целая функция типа Миттаг-Леффлера. Заметим, что при r =
2, g = 0, p=2 Hpr,s,g(Cn) превращается в
известное пространство Фока целых функций, а (1) принимает вид При n=1 и g = r-2 представление (1) впервые было
установлено в работах [2,3].
В[4] было получено следующее обобщение
формулы (2) для функций f О C1(Cn) (но, естественно, подчиненных определенным
условиям роста):
Возникает естественный вопрос: подобно тому,
как (3) обобщает формулу (2) на случай уже гладких (а не
голоморфных) функций, можно ли в таком же духе обобщить представление (1)? При
n=1 это было сделано в работе [5]. Целью настоящей заметки является получение
весового [`(¶)]-интегрального
представления в Cn при n > 1.
Предварительно введем некоторые обозначения.
Для произвольных z,w О Cn (z № w) положим Теорема 1. а) При
фиксированном z О Cn
ядро F(z,w) непрерывно по w О
Cn\{z} и остается ограниченным при w® z (w № z).
б) При фиксированном (сколь угодно малом) e > 0 в) При z № 0 и фиксированном
(сколь угодно малом) e > 0 г) Если g і 2, r > 0 или g = 0, r і
2, то при фиксированном z О Cn F(z,w) является функцией
класса C1 от w О Cn\{z} и при этом Теорема 2. Пусть n і 1, 1 < p < +Ґ, s > 0 и m = (g + 2n)/r, где либо g і 2, r
> 0, либо g = 0, r і 2. Тогда справедливо интегральное представление вида а) f О Lpr,s,g(Cn);
б) при фиксированном z О Cn функции
Замечание. Если
Институт математики НАН РА
Через
Hpr,s,g(Cn) обозначим
подпространство целых функций. В работе [1] было установлено, что функции f
О Hpr,s,g(Cn) допускают интегральное представление вида
![]()
где
f(z)=
rsm
2pn·
у
х
Cn f(w)e-s|w|r·|w|g·E(n)r/2(s2/r < z,w > ;m)dm(w), z О Cn, (1)
![]() a
a
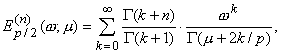
![]()
f(z)=
sn
pn·
у
х
Cn f(w)e-s|w|2·es < z,w > dm(w), z О Cn. (2)
f(z)=
sn
pn·
у
х
Cn f(w)·e-s|w|2·es < z,w > dm(w)-
-
G(n)
pn·
у
х
Cn <
¶
f(w),w-z > e-s|w|2·es < z,w > ·
n-1
е
p=0
sp
p ! · |w - z|2n-2p, z О Cn, (3)
где
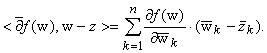
При
z № 0 через [z] обозначим комплексную прямую,
порожденную вектором z. Пусть r, s > 0, g і 0 и m = (g + 2n)/r. Рассмотрим функции
a=
< z, w - z >
|w - z|, c=
< w, w - z >
|w - z|, d =
|z|2 · |w - z|2 - | < z, w - z > |2
|w - z|2.
y(w)=(w -
_
a
)n-1·E(n)r/2(s2/r·(wa + d);m), w О C,
Кроме
того, положим (x і 0):
y(n)(w) є
dny(w)
dwn
, n =
0,1,2,ј.
j(x) = e-s(x+d)r/2 · (x + d)g/2,
Наконец,
определим ядро
Fk(x) =
1
G(k)·
+Ґ
у
х
x j(t) · (t - x)k-1dt, k = 1,2,ј.
Некоторые из свойств ядра F(z,w) описывает следующая
F(z,w)=
rsm
2G(n)·
м
н
о
n-1
е
n =
0 Fn+1(0) · y(n)(0) ·
·
n-1-n
е
m=0 Cnm+1+n · (-a)n-1-n-m · cm -
1
c(c - a)n·
|c|2
у
х
0 j(x) · y(
x
c)dx
ь
э
ю
. (4)
|F(0,w)| <
const
· e-(s-e)|w|r, |w|® +Ґ.
|F(z,z + w)| <
const
· |w|n-1, w О
[z], |w|® +Ґ,
|F(z,z + w)| <
const
· e-(s-e)|w|r, w^[z], |w|® +Ґ.
<
¶
w F(z,w),w - z > є -
rsm
2G(n)· E(n)r/2(s2/r · < z,w > ;m)e-s|w|r · |w|g · |w - z|2n, w О Cn\{z}.
для каждой функции f О C1(Cn), такой
что:
f(z)=
rsm
2pn·
у
х
Cn f(w)e-s|w|r · |w|g · E(n)r/2(s2/r < z,w > ;m)dm(w)-
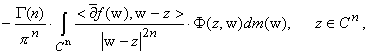
(5)
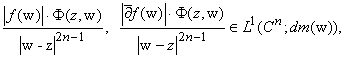
где
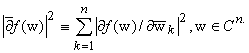
![]() ,
(5) переходит в (1). При n і 1, g = 0 и r = 2 (5) совпадает с (3).
,
(5) переходит в (1). При n і 1, g = 0 и r = 2 (5) совпадает с (3).
1. Джрбашян М.М., Карапетян А.О. - Изв. АН Армении. Математика. 1991. Т. 26. N1. С. 3-19.
2. Джрбашян М.М. - ДАН АрмССР. 1947. Т. 7. N5. С. 193-197.
3. Джрбашян М.М. - Сообщ. Ин-та матем. и мех. АН АрмССР. 1948. Вып. 2. С. 3-40.
4. Berndtsson B., Andersson M.
- Ann. Inst. Fourier. 1982. V. 32. N3. P. 91-110.
5. Джрбашян М.М. - Изв. АН Армении. Математика. 1993. Т. 28. N1.