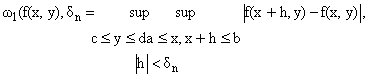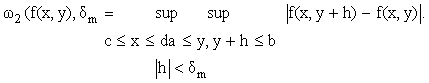ВЫЧИСЛИТЕЛЬНАЯ ТЕХНИКА
УДК 615.47
А.А.Аракелян, А.Г. Кардашян
Сплайн обработка двумерных медико-биологических
сигналов
(Представлено академиком А.А.Терзяном 26/VIII
2002)
В работах [1-5] предложены методы
спектрального анализа сигналов, основанные на применении итеративных сплайнов. В
[3-5] рассматриваются численные методы спектрального анализа одномерных
сигналов. Однако известно, что анализ электроретинограммы (ЭРГ) или
реогепатограммы (РГГ) [6] необходимо осуществлять одновременно с использованием
электрокардиограммы (ЭКГ). Следовательно, результаты [1-2] невозможно применять
для реализации спектрального анализа ЭРГ и РГГ. Необходимость создания методов
спектрального анализа двумерных сигналов определяет задачу, решению которой
посвящена данная работа.
Изучены методы численного решения задач
спектрального анализа, а также их алгоритмическая и программная реализация.
Техническая реализация осуществлена на базе сигнального процессора DSP56F803
фирмы Motorola [7].
Определения и обозначения. Пусть в прямоугольной области W = [a,b]×[c,d]
[8] введена сетка D = Dx × Dy, где
|
| Dx : a = x0 <
x1 < ј <
xN = b, | |
| Dy : c = y0 <
y1 < ј <
yM = d, | | |
| |
(1) |
делящая область на прямоугольные
ячейки, и известны значения функции
fi,j = f(xi,yj). Через Ck,l[W] обозначим множество непрерывных на W функций f(x,y), имеющих непрерывные частные производные
порядка не выше k по x и l по y.
Для каждой элементарной ячейки Wi,j = [xi,xi+1] × [yj,yj+1]
определим функцию Si,j(x,y) двумерного кубического сплайна
| Si,j(x,y) = |
3
е
a = 0
|
|
3
е
b = 0
|
cabi,j(x - xi)a(y - yj)b. | |
(2) |
Далее для той же ячейки Wi,j = [xi,xi+1] × [yj,yj+1]
определим сплайн преобразование Фурье
| Hi,j(w1w2) = |
xi+1
у
х
xi
|
|
yj+1
у
х
yj
|
Si,j(x,y)e-jw1xe-jw2y, | |
(3) |
позволяющее вычислить значения
Hi,j(w1w2), i = 0,1,јN;
j = 0,1,јM. Отсюда преобразование Фурье во всей области
W = [a,b] × [c,d] будет иметь вид
| H(w1w2) = |
N
е
i=0
|
|
M
е
j=0
|
Hi,j(w1w2). | |
(4) |
Оценка точности аппроксимации. Положим
| E = B0[w1(f(x,y),Dn) + w2(f(x,y),Dm)], | |
где
B0 абсолютная величина, не зависящая от функции f(x,y) и сетки Dn,m,
Пусть Hf(w), Hs(w) -
преобразования Фурье соответственно исходной и сплайн аппроксимации изучаемой
функции.
Имеет место
Теорема. Если функция
f(x,y) О Ck,i[W]
определена на сетке (1) и удовлетворяет периодическим краевым условиям (т.е
является (b-a) периодической по x и (d-c) периодической по y), то
| |Hf(w) - Hs(w)| Ј E(b - a)(d - c). | |
(6) |
Доказательство. Так как
S2(x,y) интерполирует функцию f(x,y) О
Ck,l[W] на сетке Dn,m и удовлетворяет краевым периодическим
условиям, то
| ||f(x,y) - S3(x,y)||
Ј B0[w1(f(x,y),Dn) + w2(f(x,y),Dm)], | |
(7) |
где
| ||Dn|| = |
max
0 Ј
i Ј n+1
|
|xi+1 - xi|, ||Dm|| = |
max
0
Ј i Ј n+1
|
|yi+1 - yi| | |
(8) |
Из (6) следует, что правая часть неравенства
(7) не зависит от функции f(x,y) [8].
Так как ||f(x,y) - S3(x,y)||C(В) =
max |f(x,y) - S3(x,y)|, то неравенство
(7) можно записать как |f(x,y) - S3(x,y)| Ј E.
a Ј x Ј b
c Ј y Ј d
Следовательно,
|
b
у
х
a
|
|
d
у
х
c
|
|f(x,y) - S3(x,y)|e-jw1xe-jw2ydxdy Ј |
b
у
х
a
|
|
d
у
х
c
|
|Ee-jw1xe-jw2y|dxdy, | |
|
к
к |
b
у
х
a
|
|
d
у
х
c
|
f(x,y)e-jw1xe-jw2ydxdy - |
b
у
х
a
|
|
d
у
х
c
|
S3(x,y)e-jw1xe-jw2ydxdy |
к
к |
Ј E(b - a)(d - c). | |
Отсюда |Hf(w) - HS(w)| Ј E(b - a)(d - c), что и требовалось
доказать.
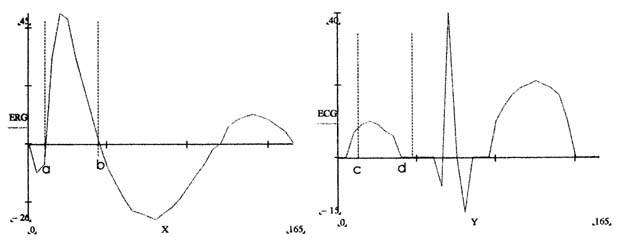
Численный пример. В качестве
примера рассмотрим функцию F(x,y) (рис.2), полученную линейной комбинацией ЭРГ и
ЭКГ, приведенных на рис.1.
а) электроретинограмма
б) электрокардиограмма
Рис.1
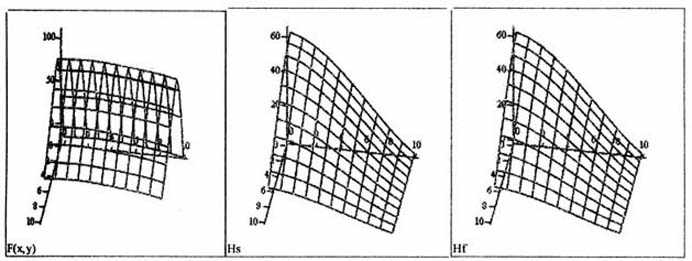
На рис. 3 приведено сплайн преобразование
Фурье (4) во всей области [a,b] × [c,d].
Для сравнения на рис.4 приведено
преобразование Фурье функции, аппроксимированной при помощи интерполяционных
формул Лагранжа, вычисленное с помощью программного пакета MathCad Professional
2001.
Рис.2
Рис.3
Рис.4
Результаты численных экспериментов,
показывают, что погрешность численного метода не превышает 1-2%.
Государственный инженерный университет
Армении
Литература
1. Ларсен Р.Д., Крофорд Е.Ф.,
Смит Р.У. - ТИИЭР. 1977. Т.65 N5.
С.247-250.
2. Малинин Л.А.
- Новости медицинской техники. 1980. вып 2. С.
25.
3. Arakelian A., Agaian S.
- Cybernetics and system research. 1984. N2. North Holland.
4. Slonim M.A. - Proc. of the IEEE. 1979. V. 67. N6.
P.953-954.
5. Usmani R.A.,
Winnipeg and Sakai M., Kagoshima, - Computing. 1996. V. 56.
P.87-93.
6. Шамшинова А.М.,
Волков В.В. Функциональные методы исследования в
офтальмологии. М. Медицина. 1998. 416с.
7.
Personal ECG monitor using DSP56F803/5. Application Brief.
http://e-www.motorola.com/brdata/PDFDB/docs/BR1560.pdf
8. Стечкин C.Б., Субботин Ю.Н.
Сплайны в вычислительной математике. М. Наука. 1976.
248с.
|