МЕХАНИКА
УДК 593.3
Академик М. А. Задоян
Задача Гадолина для конических труб
(Представлено 6/V 2002)
Одним из способов повышения прочности
составных цилиндрических труб является соединение их при горячей посадке таким
образом, чтобы внутренний диаметр охватывающей трубы был несколько меньше
наружного диаметра охватываемой трубы. После запрессовки на поверхности
прилегания возникают силы трения, препятствующие их взаимному перемещению.
Прочность толстостенной составной цилиндрической трубы можно увеличить почти
вдвое, используя метод Гадолина [1,2]. В настоящей работе предлагается способ
для повышения прочности толстостенных конических труб, основанный на идее
Гадолина.
1. Напряжение в конической
трубе. Предварительно рассмотрим толстостенную коническую трубу из
несжимаемого упрочняющегося по степенному закону материала, находяшегося под
воздействием равномерно распределенных сил на внутренней и внешней конических
поверхностях sq = -p1, -p2 при q = a, b. Полагаем, что касательные
напряжения как на поверхностях, так и по всему объему трубы равны нулю.
Принимаем равным нулю также продольное перемещение. Такое
напряженно-деформированное состояние можно представить, с использованием [3], в
следующем виде: отличные от нуля компоненты-
| sr = sq + 3AkX |
cosq
sin2q
|
, sj = sq + 6AkX |
cosq
sin2q
|
, | |
| sq = -p1 + 6Ak |
q
у
х
a
|
X |
cos2q
sin3q
|
dq, X = 3m-1|A|m-1 |
cosm-1q
sin2(m-1)q
|
, | |
| v = |
3Ar
sinq
|
, a
Ј q Ј b. | |
Используя граничные условия на внешней
поверхности q = b и вводя
обозначение
| w(x,y) = |
y
у
х
x
|
|
cosm+1q
sin2m+1q
|
dq, | |
(1) |
будем иметь
| A|A|m-1= |
p1-p2
2k3mw(a, b)
|
. | |
Для компонентов напряжений и перемещения
получаем
|
| sq = -p1 + (p1 - p2) |
w(a,q)
w(a,b)
|
, sr = |
1
2
|
(sq + sj), | |
| sj = sq + |
p1 - p2
w(a, b)
|
|
cosmq
sin2mq
|
, a Ј q Ј b, | | |
| |
(2) |
| v = |
(2k)1/m
|
|
|p1 - p2|1/m
w1/m(a, b)
|
|
r
sinq
|
. | |
(3) |
Если совершить предельный переход q ® 0, r ® Ґ, rq =
r =
const, и перейти из
сферической в цилиндрическую систему координат rtz, то
sq(q) переходит в sr(r), sr- в sz,
sj(q) - в st(r), v(q) - в u(r). Радиусы внутренней и внешней цилиндрических поверхностей
обозначим a и b; полагая ar ®
a, br ® b, из (2)-(3) получаем
|
| sr = -p1 + |
p1 - p2
W
|
|
й
к
л
|
1 - |
ж
з
и
|
a
r
|
ц
ч
ш
|
2m
|
щ
ъ
ы
|
, sz = |
1
2
|
(sr + st), | |
| st = |
1
W
|
|
й
к
л
|
p1 |
ж
з
и
|
a
b
|
ц
ч
ш
|
2m
|
- p2 + (2m - 1)(p1 - p2) |
ж
з
и
|
a
r
|
ц
ч
ш
|
2m
|
щ
ъ
ы
|
, | |
| u = |
й
к
л
|
|
m(p1 - p2)
kW
|
щ
ъ
ы
|
1/m
|
|
a2
p
|
, W = 1 - |
ж
з
и
|
|
a
b
|
ц
ч
ш
|
2m
|
. | | |
| |
Формулы для напряженно-деформированного
состояния цилиндрической трубы впервые получены А. Надаи [4] в 1922 г.
2. Составная коническая
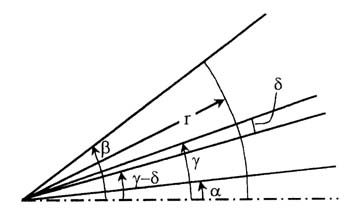
труба. Рассмотрим две конические трубы из одного и того же материала. Для
первой (внутренней) трубы величины обозначаем с индексами i = 1, а для второй
(внешней) - i = 2. Первая труба ограничена коническими поверхностями: внутренней
поверхностью q = a и внешней
поверхностью q = g (рис.1).
Вторая труба ограничена внутренней q = g - d и
внешней q = b коническими
поверхностями. Величина d > 0, угол натяга
определяется в ходе рассмотрения задачи.
Нагреваем вторую трубу так, чтобы первая
свободно входила в нее. После остывания получаем составную монолитную трубу с
внутренней q = a и внешней
q = b коническими
поверхностями. Между трубами возникает контактное давление p*,
величина которого также подлежит определению. Внутренний угол второго конуса
увеличивается, а внешний угол первого уменьшается.
Рис 1.
Если коническая труба имеет внутренние и
внешние конические поверхности соответственно q = x и
q = y, напряженное состояние согласно (2) с
рассмотренными внешними нагрузками представится в виде
|
| sq = -p1 + (p1 - p2) |
w(x,q)
w(x,y)
|
, sr = |
1
2
|
(sq + sj), | |
| sj = -p1 + (p1 - p2) |
w(x,q)
w(x,y)
|
+ |
p1 - p2
w(x,y)
|
|
cosmq
sin2mq
|
, x Ј q Ј
y. | | |
| |
(4) |
Перемещение согласно (3) будет
| v = |
(2k)1/m
|
|
|p1 - p2|1/m
w1/m(x,y)
|
|
r
sinq
|
, x Ј
q Ј
y. | |
(5) | На
контактной поверхности имеем условие совместимости перемещений
| v2(r,g) - v1(r,g) = D(r), | |
(6) | где D(r) -
неизвестный натяг, подлежащий определению.
Применяя формулу (5) для внешней трубы и
полагая p1 = p* и p2 = 0, а также x = g, y = b и q
= g, будем иметь
| v2(r,g) = |
r
sing
|
|
ж
з
и |
|
p*
2k
|
ц
ч
ш |
1/m
|
|
1
w1/m(g,b)
|
, | |
(7) | где p* контактное
давление между трубами после посадки.
Для первой трубы, полагая p1 = 0,
p2 = p*, а также x = a, y = g и q = g,
из (5) находим
| v1(r,g) = - |
r
sing
|
|
ж
з
и |
|
p*
2k
|
ц
ч
ш |
1/m
|
|
1
w1/m(a,g)
|
. | |
(8) |
Подставляя выражения (7) и (8) в (6) и
принимая D(r) = dr, где d - пока неизвестный угол, характеризующий натяг конических
труб, подлежащий определению, находим соотношение между контактным давлением и
углом натяга:
| p* = 2kdmsinmg |
w(a,g)w(g,b)
yw(a,b)
|
, | |
(9) | где
| y = |
1
w(a,b)
|
[w1/m(a,g) + w1/m(g, b)]m. | |
(10) | Заметим, что при m = 1 имеем y = 1.
3. Напряжения в составной
конической трубе. Пусть рассматриваемая составная коническая труба
находится под воздействием давления p. Полагая в (4) p1 = p,
p2 = 0, x = a, y = b,
получаем
|
| s0q = -p |
w(q, b)
w(a, b)
|
, | |
| s0j = |
p
w(a, b)
|
|
й
к
л
|
cosmq
sin2mq
|
- w(q, b) |
щ
ъ
ы
|
, a Ј q Ј b, | | |
| |
(11) | где функции w(q, b)
определяются согласно (1). Перемещение согласно (5) будет
| v = |
ж
з
и |
|
p
2k
|
ц
ч
ш |
1/m
|
|
1
w1/m(a, b)
|
|
r
sinq
|
, a
Ј q Ј b. | |
(12) | В случаe m = 1 из (1) имеем
| w(x,y) = |
1
2
|
|
ж
з
з
з
з
и
|
|
cosx
sin2 x
|
- |
cosy
sin2 y
|
+ ln |
|
ц
ч
ч
ч
ч
ш
|
. | |
(13) |
Определим компоненты напряжения в зависимости
от давления p* для внутренней трубы: полагая в (4) p1 = 0,
p2 = p*, а также x = a, y = g при a Ј
q Ј g, получаем
| s*q1(q) = -p* |
w(a,q)
w(a,g)
|
, s*j1(q) = - |
p*
w(a,g)
|
|
й
к
л |
|
cosmq
sin2mq
|
+ w(a,q) |
щ
ъ
ы |
. | |
(14) |
Для внешней трубы, полагая в (4)
p1 = p*, p2 = 0, а также x = g и y = b, находим при g Ј q Ј b
| s*q2(q) = -p* |
w(q, b)
w(g, b)
|
, s*j2(q) = |
p*
w(g, b)
|
|
й
к
л |
|
cosmq
sin2mq
|
- w(q, b) |
щ
ъ
ы |
. | |
(15) |
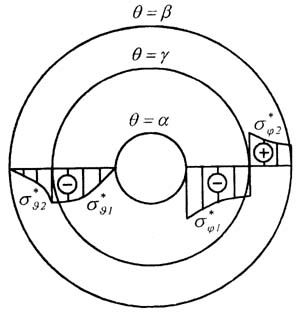
На рис.2 представлены компоненты напряжения
(14)-(15) от контактного давления. Переходя от сферической системы координат
rqj к цилиндрической rtz при r ® Ґ, q ® 0,
rq ® r
= | const из (14) при a Ј q Ј g получаем a Ј r Ј c
| s*q1 ® s*r1(r) = -p* |
1 - a2/r2
1 - a2/c2
|
, s*j1 ® s*t1(r) = p* |
1 + a2/r2
1 - a2/c2
|
, | | причем ar ® a, gr ® c. Таким же путем из (15) при
g Ј q
Ј b будем иметь c Ј r Ј b
| s*q2 ® s*r2(r) = -p* |
b2/r2 - 1
b2/c2 - 1
|
, s*j2 ® s*t2(r) = p* |
b2/r2 + 1
b2/c2 - 1
|
, | | где
принято br ® b. Выражения s*ri и s*ti соответствуют формулам для
цилиндрической трубы. Имеем также s*ri ® s*zi(r).
Рис 2.
В случае слабой нелинейности в законе
упрочнения допускаем, что приближенно справедлив закон наложения напряженного
состояния от воздействия p* и p. Суммируя компоненты напряжения
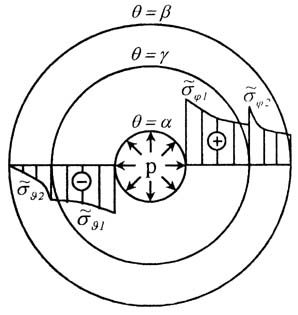
(14)-(15) с напряжениями (11), будем иметь
|
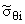 (q) = s0q(q) + s*qi(q), (q) = s0q(q) + s*qi(q), |
|
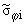 (q) = s0j(q) + s*ji(q), (q) = s0j(q) + s*ji(q), | |
(16) |
где s0q и s0j -
напряжения от давления p в интервале a Ј q Ј b, которые определяются согласно (11), а s*qi и s*ji - по
формулам (14) и (15). Величины
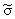 qi и qi и
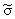 ji являются суммарными напряжениями, где i = 1 относится
к интервалу a Ј q Ј g, а
i = 2 - к интервалу g Ј q Ј b. Эти
напряжения представлены на рис. 3 согласно формулам (16). Если перейти к пределу
для цилиндрической трубы, в интервале a Ј q Ј g по-прежнему получим a Ј r Ј c ji являются суммарными напряжениями, где i = 1 относится
к интервалу a Ј q Ј g, а
i = 2 - к интервалу g Ј q Ј b. Эти
напряжения представлены на рис. 3 согласно формулам (16). Если перейти к пределу
для цилиндрической трубы, в интервале a Ј q Ј g по-прежнему получим a Ј r Ј c
|
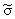
|
q1
|
® |
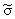
|
r1
|
(r) = -p |
b2/r2 - 1
b2/a2 - 1
|
- p* |
1 - a2/r2
1 - a2/c2
|
, | |
|
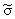
|
j1
|
® |
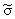
|
t1
|
(r) = p |
b2/r2 + 1
b2/a2 - 1
|
- p* |
1 + a2/r2
1 - a2/c2
|
. | |
В интервале (g Ј q Ј b) a Ј r
Ј b имеем
|
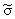
|
q2
|
® |
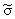
|
r2
|
(r) = -p |
b2/r2 - 1
b2/a2 - 1
|
- p* |
b2/r2 - 1
b2/c2 - 1
|
, | |
|
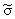
|
j2
|
® |
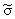 |
t2
|
(r) = p |
b2/r2 + 1
b2/a2 - 1
|
- p* |
b2/r2 + 1
b2/c2 - 1
|
. | |
Рис 3.
Определим эквивалентные напряжения
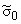 = =
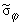 - -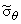 на внутренней поверхности второй трубы: на внутренней поверхности второй трубы:
|
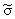
|
0
|
(a) = |
й
к
л |
|
p
w(a, b)
|
- |
p*
w(a,g)
|
щ
ъ
ы |
|
cosma
sin2ma
|
, | |
(17) |
|
|
0
|
(g) = |
й
к
л |
|
p
w(a, b)
|
+ |
p*
w(a,g)
|
щ
ъ
ы |
|
cosmg
sin2mg
|
. | |
(18) |
Для равнопрочности составной трубы принимаем
 (a) = (a) = (g). Получаем (g). Получаем
| p*= |
p
w(a, b)
|
|
ж
з
и |
|
cosma
sin2ma
|
- |
cosmg
sin2mg
|
ц
ч
ш |
|
й
к
л |
|
1
w(g, b)
|
|
cosmg
sin2mg
|
+ |
1
w(a,g)
|
|
cosma
sin2ma
|
щ
ъ
ы |
-1
|
. | |
(19) |
Далее, исключая p* из (19) и (9),
а также используя (10), находим
| d = |
ж
з
и |
|
p
2k
|
ц
ч
ш |
1/m
|
|
м
п
п
н
п
п
о
|
|
cosma
sin2ma
|
- |
cosmg
sin2mg
|
| w(a,g) |
cosmg
sin2mg
|
+ w(g, b) |
cosma
sin2ma
| |
ь
п
п
э
п
п
ю
|
1/m
|
|
w1/m(a,g) + w1/m(g, b)
w1/m(a, b)sing
|
. | |
(20) |
Таким образом, при заданных значениях
геометрических параметров a, b, g и внутреннего давления p
контактное давление p* и d определяются по
формулам (19) и (20).
4. Минимум эквивалентного
напряжения. Подставляя значение p* из (19) в (17), после
преобразований получаем
| s0(a) = p |
й
к
л |
w(a,g) |
sin2ma
cosma
|
+ w(g,b) |
sin2mg
cosmg
|
щ
ъ
ы |
-1
|
. | |
(21) |
Дифференцируя (21) по g и приравнивая к нулю, находим
| m |
b
у
х
g
|
|
cosm+1q
sin2m+1q
|
dq + |
ж
з
и |
sin2ma
cosma
|
- |
sin2mg
cosmg
|
ц
ч
ш |
|
cos2(m+1)g
sin4mg(1 + cos2g)
|
= 0. | |
(22) |
Значение g
= g*(a, b, m) определяется из (22) численным способом. В случае m = 1 из
(22) преобразованием получаем уравнение
|
ж
з
и |
cosg + |
1
cosg
|
ц
ч
ш |
|
ж
з
з
з
з
и
|
|
cosb
sin2b
|
- ln |
|
ц
ч
ч
ч
ч
ш
|
- 2 |
sin2a
cosa
|
|
cos3g
sin4g
|
-1 = 0, | |
(23) |
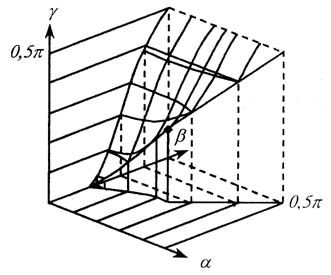
определяющее значение g* = g*(a, b). На рис.4 представлена
поверхность g* = g*(a, b), для которой g принимает
минимальное значение.
Рис 4.
Для малых значений b
из (22) или (23)
Умножая обе части этого уравнения на r и переходя к пределу ar ® a, br ® b, gr ® c, из (24) приходим к формуле
полученной еще Гадолиным для
цилиндрических труб. Представляет интерес отношение
|
s0min(a)
s00(a)
|
= w(a, b) |
sin2ma
cosma
|
|
й
к
л |
w(a,g*) |
sin2ma
cosma
|
+ w(g*, b) |
sin2mg*
cosmg*
|
щ
ъ
ы |
-1
|
, | |
(26) |
где s00(a) -
эквивалентное напряжение для однородной конической трубы a Ј b Ј g, определяющее меру снижения
эквивалентного напряжения.
Полагая a =
9o, b = 63o, согласно рис.4
определяем g* = 56o. Тогда,
принимая m = 1, из (26) находим [(s0min(a))/(s00(a))] = 0,346.
Из (26) при m = 1 переходя к пределу и
используя (25), находим
|
s0min(a)
s00(a)
|
® |
1
2
|
|
ж
з
и |
1+ |
a
b
|
ц
ч
ш |
| | степень снижения
эквивалентного напряжения для цилиндрической трубы.
Институт механики НАН РА
Литература
1. Пономарьев С.Д., Бидерман
В.Л., Лихарев К.К., Макушин В.М., Малинин Н.Н., Феодосьев В.Н. Расчеты на прочность в машиностроении. Т. 2. Машгиз. М. 1958. 975
с.
2. Феодосьев В.Н. Сопротивление материалов. М. Наука. 1972. 544
с.
3. Задоян М.А. Пространственные задачи теории пластичности. М. Наука. 1992. 384
с.
4. Надаи А. Пластичность. М. ОНТИ. 1936.
|