Reports-2003-Vol103-N1-M.S.Gabrielian

МЕХАНИКА

УДК 534.1:539.1

М.С. Габриелян, Л.А. Мовсисян

К вопросу стабилизации движения неустойчивых упругих систем

(Представлено академиком Л.А. Агаловяном 11/I 2002)

К вопросу стабилизации движения неустойчивых упругих систем
(Представлено академиком Л.А. Агаловяном 11/I 2002)

Изучается вопрос стабилизации упругих систем, на которые действует нагрузка, превосходящая эйлерово значение (задача устойчивости). При произвольном отклонении такие системы неустойчивы. Вопрос ставится следующим образом: как с помощью внешних нагрузок стабилизировать систему, при этом минимизируя некоторый функционал.
В качестве объектов рассмотрены шарнирно-опертые балка и цилиндрическая оболочка, однако ход решения поставленной задачи показывает, что такая процедура применима и для других систем. Обычно задачи стабилизации и управления рассматриваются для колеблющихся [1-3], а не экспоненциально возрастающих систем. В связи с этим принципиально также то, что минимизируемый функционал знакопеременный, но усилением управляющего воздействия удается добиться того, что система становится асимптотически устойчивой.

   1. Пусть имеется шарнирно-опертая балка, которая сжимается осевой силой, превосходящей эйлерову критическую (P > P_kp= EJp²/l²). Балке сообщаются произвольные начальные отклонения и начальная скорость.
   Уравнением движения такой системы будет

EJ ¶⁴w
¶x⁴
+ P ¶²w
¶x²
+ rS ¶²w
¶t²
= q(x,t)
(1.1)
с начальными

w к
к
к

t=0
= a(x),   ¶w
¶t
к
к
к

t=0
= b(x)
(1.2)
и краевыми

w = ¶² w
¶x²
= 0 при x = 0. x = l
(1.3)

условиями. Обозначения обычные, только надо указать, что q(x,t) - искомая нагрузка - стабилизирующее воздействие. По условию выбор q(x,t) должен обеспечивать также минимизацию некоторого функционала. В качестве такового берется

Ф =

Ґ
у
х
0

l
у
х
0

[Э + V²(q)] dxdt.

(1.4)

Под Э понимается "полная" энергия системы - сумма потенциальной и кинетической энергий (кавычки означают, что если брать полную энергию, то она, естественно, дает первый интеграл). Введением некоторого множителя в одно из слагаемых, в зависимости от того, что быстрее хочется гасить (управлять) - перемещение или скорость, можно добиться желаемого, т.е.

Э =

й
к
л

ж
з
и

¶²w

¶x²

ц
ч
ш

- P

ж
з
и

¶w

¶x

ц
ч
ш

+ brS

ж
з
и

¶w

¶t

ц
ч
ш

щ
ъ
ы

(1.5)

В этом и заключается роль параметра b. V - пока неизвестная функция от q(x,t), вид которой выяснится чуть позже.

   2. Если искать решение (1.1), удовлетворяющее условиям (1.3)

w = Ґ
е
m=1
f_m(t)sinl_mx,  l_m= mp
l
,
(2.1)
то для неизвестных f_m(t) получится

d²f_m
dt²
+ w²_m ж
з
и 1 - P
P_m
ц
ч
ш f_m= q_m(t);
(2.2)
здесь

w²_m= EJ
rS
l⁴_m,  P_m= EJl_m²,  q_m= 2
lrS
l
у
х
0
q(x,t)sinl_mxdx
(2.3)

   Замечание. Как известно, такая система, как (2.2), получается только для случая краевых условий (1.3). При иных краевых условиях получаемая система будет неканонической (в каждом уравнении присутствуют все гармоники). Для таких случаев задачу можно решить приближенно, довольствуясь несколькими членами.
   В зависимости от величины P знак скобки в (2.2) будет различным. Пусть P > P_m для первых m=k. Тогда для первых k уравнений

d²f_m
dt²
- W²_mf_m= q_m(t),  W²_m= w²_m ж
з
и P
P_m
- 1 ц
ч
ш ,   m = 1,2,ј,k.
(2.4)
Относительно функции V можно предположить, что ее разложение имеет вид

V(q) = Ґ
е
m=1

Ц

a_m

q_m(t)sinl_mx.
(2.5)

Параметры a_m, помимо того, что обеспечивают размерность в (1.4), в то же время усиливают управляющие воздействия.
Благодаря виду (2.1), (1.4) и (2.5), минимизация функционала равносильна минимизации каждой гармоники

j_m=

Ґ
у
х
0

[ -W_m²f_m²+ b(fў_m)²+ a_mf_m²] dt.

(2.6)

Искомые функции q_m(t) представляются в виде

q_m(t) = g_m⁽¹⁾f_m+ g_m⁽²⁾fў_m

(2.7)

и используется уравнение Беллмана - Ляпунова [1] для данного случая

¶W_m

¶f_m

fў_m+

¶W_m

¶fў_m

( W_m²f_m - q_m) - W_m²f_m²+ b(fў_m)²+ a_mq_m= 0

¶W_m

¶f_m

+ 2a_mq_m= 0.

(2.8)

Здесь W_m - квадратичная форма (функция Ляпунова), т.е.

W_m= A_m⁽¹⁾f_m²+ 2A_m⁽²⁾f_mfў_m+ A_m⁽³⁾(fў_m)².

(2.9)

На основании (2.7) и (2.9) из (2.7) для определения A_m⁽ⁱ⁾ и g_m⁽ⁱ⁾ получается система

2A_m⁽²⁾(W_m²+ g_m⁽¹⁾) - W_m²+ a_m(g_m⁽¹⁾)²= 0,

2(A_m⁽²⁾+ A_m⁽³⁾g_m⁽²⁾) + b + a_m(g_m⁽²⁾)²= 0,

A_m⁽¹⁾+ A_m⁽³⁾(W_m⁽²⁾+ g_m⁽¹⁾) + A_m⁽²⁾g_m⁽²⁾+ 2a_mg_m⁽¹⁾g_m⁽²⁾= 0,

A_m⁽²⁾+ a_mg_m⁽¹⁾= 0,

A_m⁽³⁾+ a_mg_m⁽²⁾= 0.

(2.10)

Для того, чтобы система была асимптотически устойчивой, достаточны требования

A_m⁽¹⁾ > 0, A_m⁽¹⁾A_m⁽³⁾ - (A_m⁽²⁾)² > 0,

a_m[b(g_m⁽¹⁾)² - W_m²(g_m²)²] - bW_m² > 0.

a_m(g_m⁽¹⁾)² - W_m² > 0.

(2.11)

Из системы (2.10) определяются искомые величины (a_m > 0)

g_m⁽¹⁾= -W_m² -

L_m

, L_m= W_m⁴-

W_m²

a_m

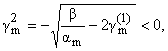
A_m⁽¹⁾= a_m

й
к
л

L_m

ж
з
и

a_m

- 2g_m⁽¹⁾

ц
ч
ш

щ
ъ
ы

1/2

> 0,

A_m⁽²⁾= -a_mg_m⁽¹⁾ > 0,

A_m⁽³⁾= -a_mg_m⁽²⁾ > 0.

(2.12)

Выбором знаков при радикалах и значений величин a_m и b можно добиться того, чтобы удовлетворялись условия (2.11). При этом нет надобности для каждой гармоники брать свою величину b. Достаточно из них взять наибольшую, тогда все условия тем более будут удовлетворены.
Характеристическое уравнение (2.4) с учетом (2.7) будет

s² - W_m²- g_m⁽²⁾s - g_m⁽¹⁾= 0,

корни которого

s_1,2= -

м
н
о

й
к
л

a_m

+ 2

ж
и

W_m²+

L_m

ц
ш

щ
ъ
ы

1/2

й
к
л

a_m

+ 2

ж
и

W_m² -

L_m

ц
ш

щ
ъ
ы

1/2

ь
э
ю

(2.13)

Так как W_m² > , то корни вещественные и отрицательные. Решение уравнения (2.4) с учетом начальных условий (1.2) и управляющее воздействие (убывающее) определятся формулами

f_m= B_m⁽¹⁾e^s₁t+ B_m⁽²⁾e^s₂t,

q_m= (g_m⁽¹⁾+ g_m⁽²⁾s₁)B_m⁽¹⁾e^s₁t+ (g_m⁽¹⁾+ g_m⁽²⁾s₂)B_m⁽²⁾e^s₂t,

B_m⁽¹⁾=

a_ms₂- b_m

s₂ - s₁

, B_m⁽²⁾=

b_m - a_ms₁

s₂ - s₁

(2.14)

3. Для m > k уже имеется система

d²f_m
dt²
+ Q_m²f_m= q_m(t), Q_m²= -W_m².
(3.1)

   Искомая функция q_m(t), минимизируемый функционал j_m и функция W_m имеют вид, как и в предыдущем пункте, однако здесь в уравнении Белламана - Ляпунова скобка во втором слагаемом должна быть заменена q_m - Q_m²f_m. Здесь уже минимизируемый функционал является знакопостоянным, поэтому можно предполагать a_m= 1, а b - любой, в частности, b = 1.
   Дальнейшая процедура совершается аналогичным образом, как в п.2. Условия асимптотической устойчивости имеют вид (2.11), а необходимые величины есть

g_m⁽¹⁾= Q_m² -
Ц

Lў_m

< 0,  Lў_m= Q_m⁴ - Q_m²,

g_m⁽²⁾= -
Ц

1 - 2g⁽¹⁾_m

< 0,

A_m⁽¹⁾= Q_m (1 - 2g⁽¹⁾_m)^1/2(Q_m² - 1)^1/2 > 0,

A_m⁽²⁾= -g⁽¹⁾_m > 0,   A_m⁽³⁾= -g⁽²⁾_m > 0.

(3.2)
Корнями характеристического уравнения будут

s_1,2= 1
2
й
л g_m⁽²⁾ ±
Ц

(g_m⁽²⁾)²+ 4g_m⁽¹⁾- 4Q_m²

щ
ы .
(3.3)
Так как дискриминант (3.3) отрицательный

s_1,2= n₁± in₂,

n₁= 1
2
g_m⁽²⁾,   n₂= [ 4Q_m² - 4g_m⁽¹⁾ - ( g_m⁽²⁾)²]^1/2,

(3.4)
решение после удовлетворения начальным условиям представится

f_m= ( a_mcosn₂t + B_m⁽³⁾sinn₂t),

q_m= {[g_m⁽¹⁾a_m+ g_m⁽²⁾(n₁a_m+ n₂B_m⁽³⁾)]cosn₂t +

       + [g_m⁽¹⁾B_m⁽³⁾+ g_m⁽²⁾(n₁B_m⁽³⁾ - n₂ a_m)]sinn₂t},

B_m⁽³⁾= b_m - n₁a_m
n₂
,

(3.5)

4. В качестве примера рассматривается балка, на которую действует сжимающая сила, равная 1.1 эйлеровой, и ей сообщается начальное отклонение в виде одной полуволны: a₁= A, b₁= a_m= b_m= 0 при m і 2. Тогда, принимая, например, b = 2 и a₁= 4W₁^-2 (W₁= 0.32w₁), необходимые параметры будут

g₁⁽¹⁾= -0.19w₁²,

A₁⁽¹⁾= 2.29w₁,

g₁⁽²⁾= -0.66w₁,

A₁⁽²⁾= 2.39,

s₁= -0.46w₁,

A₃⁽³⁾= 2.64w₁^-1,

s₂= -0.19w₁,

w₁= ж
з
и EJ
rS
ц
ч
ш 1/2

p²
l²
,

Выражения прогиба и управляющей нагрузки следующие:

w = A(1.68 - 0.68)sin px
l
,

q = -ArSw₁²(0.077+ 0.011)sin px
l

(4.1)

5. Осесиметричное движение круговой цилиндрической оболочки при осевом сжатии усилием интенсивности p при пренебрежении инерционным членом от продольного перемещения запишется [4]

D ¶⁴w
¶x⁴
+ Eh
R²
w + p ¶²w
¶x²
+ rh ¶²w
¶t²
= q(x,t),
(5.1)

здесь q(x,t) - внешнее управляющее давление. Для шарнирно-опертой оболочки решение (5.1) ищется в виде (2.1), и для f_m получится

d²f_m

dt²

+ w_m²

ж
з
и

1 -

T_m

ц
ч
ш

f_m= q_m(t);

(5.2)

здесь

w_m²= Dl_m⁴+

R²

, T_m= Dl_m²+

R²l_m²

q_m=

lrh

l
у
х
0

q(x,t)sinl_mxdx.

Как известно, критическое усилие

p_kp=

Eh²

, N =

3(1 - n²)

(5.3)

и оно реализуется по целочисленным полуволнам

m_kp=

ж
з
и

ц
ч
ш

1/2

(5.4)

Если действующее осевое усилие

p = æp_kp, æ > 1,

(5.5)

в зависимости от величины æ знак скобки в (5.2) будет положительным при 1 Ј m Ј m₁, m > m₂ и отрицательным при m₁ Ј m Ј m₂, где

m₁= m_kp

ж
и

æ -

æ² - 1

ц
ш

1/2

m₂= m_kp

ж
и

æ +

æ²+ 1

ц
ш

1/2

(5.6)

Далее, с точностью до обозначений, можно поступить, как в предыдущей задаче, только с той разницей, что уравнение типа (2.4) будет для гармоник m₁ < m < m₂, а уравнения типа (3.1) - 1 Ј m < m₁ и m > m₂.

Ереванский государственный университет
Институт механики НАН РА

Литература

     1. Красовский Н.Н. Теория управления движением. М. Наука. 1968. 475 с.
     2. Габриелян М.С. - Уч. записки ЕГУ. 1975. N2 С. 49-57.
     3. Габриелян М.С., Мовсисян Л.А. - Изв. РАН. МТТ. 1999. N6. С. 146-152.
     4. Вольмир А.С. Нелинейная динамика пластинок и оболочек. М. Наука. 1972. 432 с.