МЕХАНИКА
УДК 539.1
Ю.С. Сафарян, С.М. Погосян
Аналитическое и численное решение конкретных задач
об
узких пучках для электропроводящей магнитозвуковой
релаксирующей
среды
(Представлено чл.-кор. НАН РА А.Г.Багдоевым 27/I
2002)
В работе [1] формулируется задача расчета
нелинейных пучков в плазме, находящейся в поперечном магнитном поле, возникающая
в связи с изучением выброса излучения из пульсаров. В ней получена упрощенная
формула для безразмерного радиуса пучка на внешней поверхности пульсара. Кроме
того задача о поперечном поле возникает и при изучении нагрева плазмы
высокочастотными волнами в управляемых термоядерных реакциях [2]. В настоящей
статье проводится численный расчет задачи без упрощающих предположений в
уравнении для второй гармоники [1]. Получено восемь обыкновенных
дифференциальных уравнений для параметров пучка и дается их численный расчет для
разных значений начальной амплитуды, кривизн волн, диссипации и дисперсии.
Предположим, что квазиплоская волна
распространяется вдоль оси x. Оси координат y, z выбираются в плоскости
невозмущенной волны, и имеется осевая симметрия с радиальной координатой
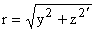 .
Обозначим через t = t1 - t, t1 = [x/(Cn)] эйконал волны в линейной
задаче, Cn- нормальная скорость линейной волны. Обозначим через
u = hy возмущенное значение магнитного поля, Hy-
невозмущенное поле. Тогда, как показано в [1], из уравнений магнитной
газодинамики можно вывести эволюционное уравнение
.
Обозначим через t = t1 - t, t1 = [x/(Cn)] эйконал волны в линейной
задаче, Cn- нормальная скорость линейной волны. Обозначим через
u = hy возмущенное значение магнитного поля, Hy-
невозмущенное поле. Тогда, как показано в [1], из уравнений магнитной
газодинамики можно вывести эволюционное уравнение
|
¶2u
¶t1¶t
|
+ |
1
2
|
C2n |
ж
з
и |
¶2u
¶r2
|
+ |
1
2
|
|
¶u
¶r
|
ц
ч
ш |
=- |
1
Cn
|
|
¶
¶t
|
|
ж
з
и |
Gu |
¶u
¶t
|
+ D |
¶2 u
¶t2
|
+ E |
¶3 u
¶t3
|
ц
ч
ш |
, | |
(1) |
где коэффициенты нелинейности G, диссипации D и дисперсии E имеют вид
|
| G = |
Cn
Hy
|
|
ж
з
и
|
|
g + 1
2
|
|
C2s
C2n
|
+ |
3
2
|
|
C2A
C2n
|
ц
ч
ш
|
, E = |
t0
Cn
|
|
(g - 1)2TK
2rCn2
|
, | |
| D = - |
1
2Cn
|
|
м
н
о
|
|
1
r
|
|
ж
з
и
|
x+ |
4
3
|
e |
ц
ч
ш
|
+ |
C2A
C2n
|
nm + |
(g - 1)2TK
rCn2
|
ь
э
ю
|
. | | |
| |
(2) |
Обозначения указаны в [1,3],
| CA2 = |
Hy2
4pr
|
,
Cn2 = Cs2 + cA2, | |
(3) |
nm = [(C2)/(4ps)], C - скорость света, s - электропроводность, Cs - скорость звука. Для
остальных параметров имеет место
| Vy = Vz = 0, hx = hz = 0, hy = - |
Hy
Cn
|
Vx, rў = |
r
Cn
|
Vx, Pў = C2srў, | |
(4) |
Vx,y,z - компоненты
скорости частиц.
Для случая квазимонохроматической волны с
основной частотой a решение (1) можно искать в виде
| u = |
1
2
|
(u1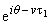 + u2 + u2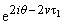 + K·
C·), + K·
C·), | |
(5) |
где q =
at - wt1, u k = uk(t1,r).
Как показано в [3,4], свободный член
U0, который следовалo бы добавить в (5), имеет для дифракционной
задачи о пучках порядок U13 и в силу малости может быть
опущен. Вычисляя производные по t1, r в (5)
и подставляя в (1), приравнивая линейные недифференцируемые члены с первой
гармоникой, можно получить дисперсионное уравнение
| w = - |
E
Cn
|
a3, n = - |
D
Cn
|
a2. | |
(6) |
Остальные члены с
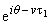 дают уравнение
дают уравнение
| ia |
¶u1
¶t1
|
+ |
1
2
|
Cn2 |
ж
з
и |
¶2
u1
¶r2
|
+ |
1
2
|
|
¶u1
¶r
|
ц
ч
ш |
= |
G
2Cn
|
a2u*1u2, | |
(7) |
где удержаны члены с второй
гармоникой, звездочкой отмечено комплексно-сопряженное значение. Члены с
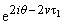 дают после
учета (6)
дают после
учета (6)
| a(4ni - 12w)u2 + 2ia |
¶u2
¶t1
|
+ |
1
2
|
Cn2 |
ж
з
и |
¶2
u2
¶t2
|
+ |
1
2
|
|
¶u2
¶r
|
ц
ч
ш |
= |
Ga2
Cn
|
u21. | |
(8) |
Полагая в (7), (8) для гауссовых
пучков
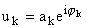 , , 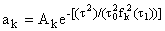 , jk = sk(t1) + , jk = sk(t1) + |
1
2Rk(t1)
|
r2, k = 1,2, | |
(9) |
где ak - действительные
амплитуды гармоник, r0 - постоянный начальный радиус пучков, можно
получить обыкновенные уравнения по переменной t1 от параметров пучка. Отделяя в этих уравнениях
члены с r0 и r2, затем разделяя действительные и мнимые
части, получим обыкновенные дифференциальные уравнения.
Вводя безразмерные переменные, обозначенные
штрихами
|
| A1 = KAў1, A2 = KAў2, t1 = |
1
a
|
tў, cos(s2 - 2s1) = C, sin(s2 - 2s1) = S, | |
|
1
R1
|
= Kў1 |
ж
з
и
|
|
a
Cn
|
ц
ч
ш
|
2
|
, |
1
R2
|
= Kў2 |
ж
з
и
|
|
a
Cn
|
ц
ч
ш
|
2
|
, |
r02
Cn2
|
a2 = rў0 2, n = anў, w = awў | |
| e-2nўtў = Eў, |
GK
Cn
|
= Gў, |
1
f21,2
|
= F1,2, K = A1(0), | | |
| |
(10) |
можно получить следующие 8
уравнений:
|
ds1
dtў
|
+ |
2F1
rў 02
|
= - |
Gў
2
|
EўAў2C, | |
(11) |
|
dAў1
dtў
|
+Aў1Kў1 = |
Gў
2
|
SAў1Aў2Eў, | |
(12) |
|
dKў1
dtў
|
- |
4
rў 04
|
F12 + Kў 21 = GўEўAў2 |
ж
з
и |
|
C
rў 02
|
F2 + S |
Kў2 - 2Kў1
2
|
ц
ч
ш |
, | |
(13) |
|
1
rў 02
|
|
dF1
dtў
|
+ Kў1 |
2
rў 02
|
F1 = Aў2 |
GўEў
2
|
|
ж
з
и |
|
1
rў 02
|
F2S - C |
Kў2 - 2Kў1
2
|
ц
ч
ш |
, | |
(14) |
| 2Aў2 |
ds2
dtў
|
+ 12wўAў2 + |
2
rў 02
|
Aў2Kў2 = - GўAў 21C, | |
(15) |
| 2 |
dAў2
dtў
|
+ 4nўAў2 + 24GўAў2 + Aў2Kў2 = - GўAў 21S, | |
(16) |
| Aў2 |
dKў2
dtў
|
+ |
1
2
|
Aў2 |
ж
з
и |
|
4
rў0 2
|
F22 - K2ў 2 |
ц
ч
ш |
= - GўAў 21 |
ж
з
и |
S |
2Kў1 - Kў2
2
|
+ |
-2F1 + F2
rў 02
|
C |
ц
ч
ш |
, | |
(17) |
| 2Aў2 |
1
rў 02
|
|
dF2
dtў
|
+ |
2Aў2Kў2F2
rў 02
|
= - GўAў 21 |
ж
з
и |
C |
2Kў1 - Kў2
2
|
- S |
-2F1 + F2
rў0 2
|
ц
ч
ш |
. | |
(18) |
Уравнения (11)-(18) решаются при начальных
условиях, следующих из значения решения для падающей волны в форме
t1 = 0 u1 = K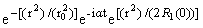 | |
При этом уравнения (15), (17), (18) при t1=0, если считать Aў2(0)=0, дают следующие граничные условия:
|
| C(0) = 0, Kў2(0) - 2Kў1(0) = 0, F2(0) = 2F1(0), s2(0) = 2s1(0) + |
p
2
|
, | |
| tў = 0, Aў1 = 0.1, Aў2 = 0.01, Kў1 = |
1
R0
|
|
ж
з
и
|
|
Cn
a
|
ц
ч
ш
|
2
|
, Kў2 = 2 |
1
R0
|
|
ж
з
и
|
|
Cn
a
|
ц
ч
ш
|
2
|
, | |
| F1 = 1, F2 = 2, s1 = 0, s2 = |
p
2
|
. | | |
| |
(19) |
Полученное по (6) значение w или wў,
т.е. дисперсии за счет теплопроводности, весьма мало. Чтобы получить конечную
дисперсию, можно использовать уточненное дисперсионное уравнение для плазмы [5],
которое приводится к виду
W2 =
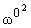 - -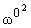 |
k2c2
w02
|
|
CA2
CS2 + CA2
|
, w0 = kCn, W = w0 + w, | |
где
w0 - плазменная частота [5], k - волновое
число,
| w = - |
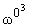
2Cn2
|
|
C2
w02
|
|
CA2
CS2 + CA2
|
. | |
Для случая большой дисперсии |wt1| >> 1 можно в
(8) отбросить дифференцируемые члены с U2, при этом имеет место |u2| << |u1|, |uk| << |uk-1| и получится
| u2 = |
Gau12
4Cn(-3w + ni)
|
. | |
(20) |
Уравнение (1) приводится к
нелинейному уравнению Шредингера
| ia |
¶u1
¶t1
|
+ |
1
2
|
Cn2 |
ж
з
и |
|
¶2u1
¶r2
|
+ |
1
2
|
|
¶u1
¶r
|
ц
ч
ш |
= (æ1 + æ2i)|u1|2u1, | |
(21) |
где
| z = |
G2a3
8Cn2
|
|
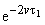
9w2 + n2
|
. | |
(23) |
Отыскивая решение (21) в виде (9),
можно получить соотношения
|
ds1
dt1
|
= - |
2Cn2
ar02f12
|
- æ |
b12
af12
|
, | |
(25) |
|
1
R1
|
= |
a
Cn2f1
|
|
df1
dt1
|
+ |
æ2b12
Cn2f12
|
, | |
(26) |
|
d2f1
dt12
|
= |
x
f13
|
+ |
2æn
b12
af1
|
, | |
(27) |
где
| x = a-2(4Cn4r0-4 + 4æ1b12Cn2r0-2 - æ22b14). | |
(28) |
Таким образом в случае большой
дисперсии получается уравнение (27), которое нужно решать при граничном условии,
следующем из (26):
| f1(0) = 1, |
df1(0)
dt1
|
= F, F = |
Cn2
a
|
|
ж
з
и |
R0-1 - |
æ2
Cn2
|
b12 |
ц
ч
ш |
. | |
(29) |
При этом æ1,2 является функцией от
t1. В случае малых nt1 следует в правой
части (27) отбросить второе слагаемое и считать e-nt1=1, тогда (27), (28) интегрируется и дает
формулу (2.15) из [6].
В переменных (10)
| F1-1 = (Fў 2 + xў) |
ж
з
и |
tў + |
Fў
Fў 2 + xў
|
ц
ч
ш |
2
|
+ |
xў
Fў 2 + xў
|
, | |
(30) |
где Fў = kў1(0) - æў2, xў = [4/(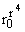 )] + æў1[4/(
)] + æў1[4/(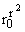 )] - æ2ў 2,
)] - æ2ў 2,
| æў1 = - |
3wў
8
|
|
Gў 2Eў
9wў 2 + (nў + 6)2
|
, æў2 = -(nў + 6) |
Gў 2
8
|
|
Eў
9wў 2 + (nў + 6)2
|
. | |
(31) |
Уравнения коротких волн для
произвольной однородной среды получены в [7].
Рассмотрим расчет типичных задач для
пульсаров [1], электролитов и термоядерных реакторов [2].
1. Для задачи о действии магнитного поля на
пучок, распространяющийся от внутренней поверхности звезды, представляющей сферу
радиуса R0[(a)/(Cn)] = 106 см при начальном
радиусе пучка r0 = 104 см, причем
Cn = 1010 см/с, a =
106 1/с [1], на основании (10) можно полагать rў0 = 2, Kў1 = [2/100], Kў2 = [4/100], w =
[1/2] · 10-3 1/с. Кроме значения nў = 0 для звезды рассмотрены значения
nў = 0.03 для электролитов, для
которых s = 1.3·107 1/с,
[(CA)/(Cn)] = 1,
C2 = 1021 см2/с2. Используя
граничные условия (19), можно рассчитать (11)-(18) начиная от x = 0 до x = l или,
поскольку на внешней границе l = 105 см, tў = a[l/(Cn)], интегрировать от tў = 0 до tў = 20. Значения
F1, Aў1 Aў2 приведены в таблице.
Для вычисления
F1 = [1/(f12)] по приближенной формуле (30)
следует рассчитать w = [1/2]·10-9, nў = [1/2]10-12, и поскольку
дисперсия и диссипация весьма малы, полученная в предположении | w[l/(Cn)]| >> 1 формула (30) в нелинейном
варианте не пригодна, в линейном же случае при предположении æ1,2 = 0
она пригодна и при tў = 20 дает
f1 = 10, при этом из-за малой нелинейности (30) использована при
æ1,2 = 0. Это значение совпадает с приведенным в таблице.
2. Cn=1010 см/с,
a = 108 1/с. Тогда rў0 = 102, Kў1 = 10-4,
Kў2 = 2·10-4. Кроме того nў = 0, w = 0, поэтому нелинейная
формула (30) не применима. В линейном случае (30) дает f1 » 1.2, что качественно согласуется с таблицей.
3. Cn = 1010 см/с,
a = 107 1/с. Расчеты
по формулам (11)-(18) приведены в таблице. Нелинейная
формула (30) снова не применима. Линейная формула (30) (æ1,2 = 0)
дает при a[l/(Cn)] = 10-2, f12 = 5,
что согласуется с таблицей.
|
|
 |
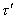 |
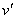
|
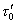 |
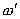 |
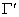 |
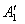 |
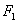 |
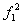 |
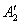 |
|
 |
 |
20 |
0 |
2 |
0 |
0.12 |
0.089 |
0.97×10-2 |
1.03×102 |
-0.13×10-2 |
|
 |
 |
103 |
0 |
102 |
0 |
 |
0.9 |
0.81 |
1.3 |
-0.71×10-2 |
|
 |
 |
103 |
0 |
102 |
0 |
 |
0.83 |
0.68 |
1.47 |
0.11×10-1 |
|
 |
 |
103 |
0 |
102 |
0 |
 |
0.89 |
0.80 |
1.25 |
-0.13×10-2 |
|
 |
 |
102 |
0,03 |
10 |
0 |
0.12 |
0,43 |
0.19 |
5.26 |
0.27×10-1 |
|
 |
 |
102 |
0,03 |
10 |
0 |
 |
0,44 |
0.19 |
5.26 |
0.28×10-3 |
|
 |

|
20 |
0 |
2 |

|
0.12 |
0.98 |
0.96×10-2 |
1.05 |
0.63×10-3 |
|
 |
 |
102 |
0 |
10 |

|
0.12 |
0.28 |
0.76×10-2 |
17.6 |
-0.12×10-1 |
|
 |
 |
102 |
0 |
10 |

|
 |
0.35 |
0.12 |
8.3 |
0.19×10-2 |
|
 |
 |
102 |
0 |
10 |

|
 |
0.35 |
0.12 |
8.3 |
0.22×10-3 |
Расчеты для термоядерной плазмы можно проводить по типичным значениям
параметров, взятых из [2].
4. Cn = 107 см/с,
a = 2 · 106 1/с.
l = 102 см, r0 = 10 см, rў0 = 2, s =
3 · 1017 1/с, nў = [5/3]10-6, n = [5/3]. Кроме того начальная кривизна волны
[1/(R0)][(Cn)/(a)] = [1/(102)] 1/см. Тогда Fў = [1/10] 1/с, w = -[1/4]103 1/с, wў = -[1/4000]. В формуле (30) æў1 = 2, æў2 = 0,
f1( a[l/(Cn)]) = 34. По линейному
варианту формулы (30), где æў1,2 = 0,
f1( a[l/(Cn)]) = 10, что близко к
таблице. Последние три строки таблицы соответствуют значениям, приведенным в
п.5.
5. Cn = 107 см/с,
a = 107 1/с, при этом w = -[1/4]106 1/с,
wў = -[1/40], rў0 = 10,
[1/(R0)][(Cn)/(a)] = [1/(102)], Fў = [1/(102)]. Поскольку | [(wl)/(Cn)]| >> 1, формула (30) применима и
расчеты по (30) дают xў = 5·10-4,
f12([(al)/(Cn)]) = 7.
Линейный подход, при котором æў1,2 = 0, дает
f12([(al)/(Cn)]) = 6.
Таблица согласуется также с расчетами
звуковых пучков [8], проведенными для (1) при E = 0.
Граничные значения в формуле (19) для
вариантов 1-3 дают kў1=10-6[(Cn)/(a)],
kў2 = 2·106[(Cn)/(a)], а для
вариантов 4, 5 kў1 = 10-2[(Cn)/(a)],
kў2 = 2·10-2[(Cn)/(a)].
Горисский филиал Государственного
инженерного университета Армении
Литература
1. Багдоев А.Г., Седракян Д.М.
- Астрoфизика. 2001. Т. 44. С.
139.
2. Голант В.Е. Жилинский
Я.М., Сахаров И.Е. Основы физики плазмы. М. Атомиздат. 1977.
384 с.
3. Багдоев А.Г., Шекоян
А.В. - Акустический журнал. 1999. Т. 45.
С. 149.
4. Багдоев А.Г.,
Петросян Л.Г. - Изв. АН АрмССР. Механика. 1983. Т. 36.
С.3.
5. Франк-Каменецкий Д.А.
Лекции по физике плазмы. М. Атомиздат. 1964. 283
с.
6. Багдоев А.Г., Гургенян А.А.
- Изв. АН АрмССР. Механика. 1986. Т. 39. С.
16.
7. Минасян М.М. - ДАН АрмССР. 1972. Т. 55. С. 123.
8.
Бахвалов Н.С., Жилейкин Я.М., Заболотская Е.А. Нелинейная теория звуковых пучков. М. Наука. 1982. 176с.
![]() + u2
+ u2![]() + K·
C·),
+ K·
C·),![]() дают уравнение
дают уравнение ![]() дают после
учета (6)
дают после
учета (6) ![]() ,
, ![]() , jk = sk(t1) +
, jk = sk(t1) +![]()
![]() -
-![]()
![]()
![]()
![]() )] + æў1[4/(
)] + æў1[4/(![]() )] - æ2ў 2,
)] - æ2ў 2,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()