МАТЕМАТИКА
УДК 518.9
В.С. Амбарян
Связь между стратегиями погонного преследования и
параллельного
сближения при прямолинейном движении преследуемого
(Представлено академиком Ю.Г. Шукуряном 16/X
2002)
Пусть преследователь P и преследуемый E
перемещаются в плоскости с постоянными по модулю скоростями a и b (a > b) соответственно, и при этом
в начальный момент времени t=0 игрок P находится в начале координат P(0)={0,0},
а игрок E в точке с координатами E(0)={a,0}.
Допустим, что игрок P в момент времени t=0
применяет стратегию погонного преследования [1,2], а игрок E выбирает любое
прямолинейное движение, тогда, как показал В.Д. Ширяев [2], уравнение кривой
множества точек поимки (встречи) имеет вид:
| ((x-a)2+y2-ab2/(a2-b2)(x-a))2=(aab/(a2-b2))2((x-a)2+y2). | |
(1) |
Преобразуем уравнение (1) следующим
образом:
| (a2-b2)((x-a)2+y2)-ab2(x-a)=aab |
|
________
Ц(x-a)2+y2
|
, | |
| a2((x-a)2+y2)-b2x2+2ab2x-a2b2-b2y2-ab2x+a2b2=aab |
|
________
Ц(x-a)2+y2
|
, | |
| a2((x-a)2+y2)-b2(x2+y2)+ab2x=aab |
|
________
Ц(x-a)2+y2
|
. | |
Далее имеем:
| a2((x-a)2+y2)-aab |
|
________
Ц(x-a)2+y2
|
=b2(x2+y2)-ab2x, | |
| (a |
|
________
Ц(x-a)2+y2
|
-ab/2)2=b2(x2+y2)-ab2x+(ab/2)2, | |
| a |
|
________
Ц(x-a)2+y2
|
=b |
|
__________
Ц(x-a/2)2+y2)
|
+ab/2. | |
Откуда
| a2((x-a)2+y2)=b2((x-a/2)2+y2)+ab2 |
|
__________
Ц(x-a/2)2+y2
|
+(ab/2)2, | |
| a2x2-2aa2x+(aa)2+a2y2-b2x2+ab2x-(ab)2/2-b2y2=ab2 |
|
__________
Ц(x-a/2)2+y2
|
, | |
| (a2-b2)(x2+y2)-(2aa2-ab2)x+(aa)2-(ab)2/2=ab2 |
|
__________
Ц(x-a/2)2+y2
|
, | |
|
| (x-a/2)2+y2+ax-(a/2)2-(2aa2-ab2)/(a2-b2)(x-a/2)= | |
| = ab2/(a2-b2) |
|
__________
Ц(x-a/2)2+y2
|
. | | |
| |
|
| (x-a/2)2+y2+a(x-a/2)+a2/4-(2aa2-ab2)/(a2-b2)(x-a/2)= | |
| = ab2/(a2-b2) |
|
__________
Ц(x-a/2)2+y2
|
. | | |
| |
Окончательно получаем
| ((x-a/2)2+y2-aa2/(a2-b2)(x-a/2)+(a/2)2)2=(ab2/(a2-b2))2((x-a/2)2+y2). | |
(2) |
Таким образом, мы показали, что уравнения (1)
и (2) эквивалентны.
Теперь допустим, что игрок P начинает
преследование, применяя стратегию параллельного сближения с задержкой T > 0;
до момента времени T игрок P стоит в точке P(0), а игрок E движется прямолинейно
с момента t=0. Тогда уравнение кривой множества точек встречи имеет вид [3,4]
|
| (x2+y2-2aa2/(a2-b2)x+((aa)2-(abT)2)/(a2-b2))2= | |
|
| |
| |
(3) |
и представляет собой овал Декарта
[5].
Предположим, что игрок P начинает
преследование, применяя стратегию параллельного сближения с задержкой
T=(a/2)/a из точки P(T)={a/2,0}, а игрок E из точки
{a,0} движется прямолинейно. Тогда овал Декарта (множество точек встречи) имеет
вид
| 1/b |
|
________
Ц(x-a)2+y2
|
=1/a |
|
__________
Ц(x-a/2)2+y2
|
+T. | |
(4) |
После соответствующих преобразований получаем
|
| ((x-a/2)2+y2-aa2/(a2-b2)(x-a/2)+((aa/2)2-(abT)2)/(a2-b2))2= | |
| =(2ab2T/(a2-b2))2((x-a/2)2+y2). | | |
| |
(5) |
Подставляя значение T=(a/2)/a в (5), получаем уравнение (2).
Из вышеизложенного следует, что
геометрические места точек поимки (множество точек встречи) для обеих стратегий
совпадают.
Таким образом можно сформулировать следующую
теорему.
Теорема. При
прямолинейном движении преследуемого E геометрическое место точек встречи при
применении преследователем P стратегии погонного преследования совпадает с
геометрическим местом точек встречи при применении преследователем P стратегии
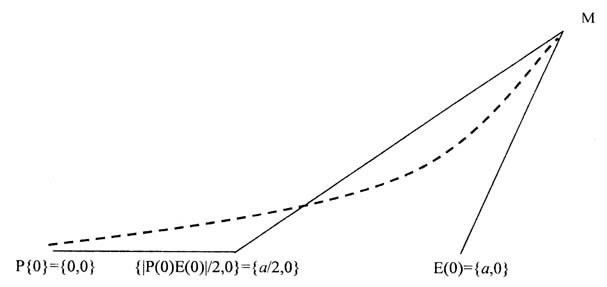
параллельного сближения с задержкой T=|P(0)E(0)|/(2a) с начальной точкой {|P(0)E(0)|/2,0}.
|
|
----------- стратегия погонного преследования,
стратегия параллельного сближения.
Иными словами, при прямолинейном движении
игрока E его поимка произойдет в одной и той же точке как в случае применения
игроком P стратегии погонного преследования, так и в случае, если игрок P
преодолеет со скоростью a половину отрезка |P(0)E(0)| и в этой точке применит
стратегию параллельного сближения (рисунок).
Ереванский научно-исследовательский
институт математических машин
Литература
1. Петросян Л.А. - ДАН СССР. 1965. Т.161. N1. С. 52-54.
2. Петросян Л.А., Томский Г.В.
Геометрия простого преследования. Новосибирск. Наука. 1983.
143 с.
3. Амбарян В.С.
- ДАН Армении. 1991. Т.92. N4. С.
147-153.
4. Амбарян В.С.
- ДАН Армении. 1992. Т.93. N4. С. 163-167.
5. Савелов А.А. Плоские кривые. М. Физматгиз. 1960. С. 293.
