УДК 515.1

   Работа посвящена бесконечномерной алгебраической топологии вещественного гильбертова пространства H.
   Допустимыми являются непрерывные отображения подмножеств из H, принадлежащие специальному классу K и его подклассу K₀; отображения этих классов кратко назовем K-отображениями и K₀-отображениями, соответственно.
   Ряд основных свойств K- и K₀-отображений и их приложений содержатся, в частности, в [1-7].

   1. Допустимые классы отображений.  Пусть H - зафиксированное вещественное гильбертово пространство и G - его произвольное открытое подмножество.
   Определение 1.  Будем говорить, что непрерывное отображение f : G ® H принадлежит классу K (относительно H) или является K-отображением, если выполнено условие:
   (K) для любой точки x₀ О G и любого e > 0 существуют окрестность U М G точки x₀, конечномерное подпространство L М H и число l такие, что если точки x,y О U и вектор x - y ортогонален L, то

|| f(x) - f(y) - l(x - y) || Ј e || x - y || .

   Определение 2.  Будем говорить, что непрерывное отображение f : G ® H принадлежит классу K₀ (относительно H) или является K₀-отображением, если выполнено условие:
   (K₀) для любой точки x₀ О G и любого e > 0 существуют окрестность U М G точки x₀, конечномерное подпространство L М H, числа l и d, 0 < d < [(p)/2], такие, что если точки x,y О U и угол между вектором x - y и подпространством L не меньше [(p)/2] - d, то

|| f(x) - f(y) - l(x - y) || Ј e || x - y || .

   Всякое K₀-отображение является K-отображением и локально удовлетворяет условию Липшица: для каждой точки x₀ О G существуют такие числа r = r(x₀) > 0 и c = c(x₀) > 0, что если точки x,y О G, || x - x₀ || < r и || y - x₀ || < r, то || f(x) - f(y) || Ј c||x - y||.
   Обратно, K-отображение локально удовлетворяющее условию Липшица, будет K₀-отображением [1,5].
   Важным характеризующим свойством K- и K₀-отображений является тот факт, что фигурирующее в условиях (K) и (K₀) число l можно выбрать так, чтобы оно зависело лишь от точки x₀, но не от числа e > 0; в результате строится заданная на G единственная непрерывная вещественная функция l(x), которую называем терминальной производной отображения f и обозначаем через l_f(x). Композиция K₀-отображений g₁ : G₁ ® G₂ и g₂ : G₂ ® H есть K₀-отображение и l_g2°g1(x) = l_g1(x)l_g2(g₁(x)) для каждой x О G₁. Композиция двух K-отображений не всегда есть K-отображение.
   Пусть теперь M - произвольное (не обязательно открытое) подмножество из H.
   Будем говорить, что непрерывное отображение f : M ® H является K- (соотв. K₀-) отображением, если существует открытое в H множество G Й M и такое K- (соотв. K₀-) отображение g : G ® H, что f(x) = g(x) для каждой x О M.
   Каждое такое отображение g будем называть K- (соотв. K₀-) продолжением отображения f.
   Пусть теперь M и N - произвольные подмножества из H. Будем говорить, что непрерывное отображение f : M ® N есть K- (соотв. K₀)- отображение, если f, рассматриваемое как отображение M в H, т.е. композиция i o f : M ® H, есть K- (соотв. K₀)- отображение, где i : N ® H - вложение. Наконец гомеоморфизм f:M @ N называем K₀-гомеоморфизмом, если оба отображения f и f^-1 суть K₀-отображения. Аналогичным образом определяется понятие K-гомеоморфизма.

   2. Множества, допускающие терминальные производные и K₀-терминальные производные.  Пусть M - произвольное (не обязательно открытое) подмножество из H.
   Определение 3.  Будем говорить, что K-отображение f : M ® H обладает терминальной производной, если ограничения на M терминальных производных l_g(x) всех K-продолжений g : G ® H отображения f совпадают между собой; получающуюся при этом заданную на M вещественную непрерывную функцию l_g(x)|M назовем терминальной производной отображения f и обозначим через l_f(x).
   Например, если M - линейное (векторное) подпространство H, то всякое K-отображение f : M ® H будет обладать терминальной производной тогда и только тогда, когда M бесконечномерно.
   Для приложений важны такие подмножества M М H, для которых всякое K-отображение f : M ® H обладает терминальной производной.
   Предложение 1.  Пусть M подмножества из H; рассмотрим условия:
   a) для каждой точки x_o О M, каждой окрестности U М M в M точки x₀ и для каждого конечномерного линейного подпространства L из H существует пара различных точек x,y О U такая, что вектор (x - y) ^ L, т.е. ограничение на U ортогонального проектора p : H ® L не инъективно;
   b) всякое K-отображение f : M ® H обладает терминальной производной;
   c) если K-отображения g_i : G_i ® H, i = 1,2, совпадают между собой на M, то на M совпадают и их терминальные производные l_g1(x) и l_g2(x).
   Тогда имеют место имплексации a ® c ® b ® c.
   Замечание 1.  Если M М H удовлетворяет условию a) предложения 1, то и его замыкание 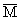в H, всякое открытое в M подмножество U М M также удовлетворяют условию a); наконец, объединение любого семейства подмножеств из H, удовлетворяющих условию a), также удовлетворяет условию a). В частности, если M удовлетворяет условию a), то таким же является и Mx[0.1].
   Определение 4.  Множество M М H, удовлетворяющее условию a) предложения 1, назовем множеством, допускающим терминальные производные.
   Лемма 1.  Пусть M М H множество, допускающее терминальные производные, f : M ® H есть K-отображение.
    Тогда для любой точки x₀ О M, любого числа e > 0 существует открытая в M окрестность V М M точки x₀ и конечномерное подпространство L М H такие, что если точки x,y О V таковы, что (x - y) ^ L, то

|| f(x) - f(y) - lf(x0)(x - y) || Ј e || x - y || .

   Теорема 1.  Пусть M М H множество, допускающее терминальные производные, в частности открытое множество в H, f : M ® H - K -отображение, а X М M - компактное подмножество. Тогда для e > 0 существуют открытое в M подмножество U Й X и конечномерное подпространство L М H такие, что если x,y О U таковы, что (x - y) ^ L, то

|| f(x) - f(y) - lf(x0)(x - y) || Ј e || x - y || .

   Теорема 2.  Пусть M М H множество, допускающее терминальные производные, f : M ® H - K-отображение, а X М M - такое компактное подмножество, на котором терминальная производная l_f(x) отображения f всюду отлична от нуля. Тогда существует конечномерное подпространство L М H такое, что
   1) если f на X постоянно, то ортопроектор p : H ® L инъективен на X, следовательно dimX < Ґ;
   2) для каждой точки x₀ О X ограничение f на подмножестве X З H_x, есть гомеоморфизм, где H_x0 = x₀ + L^{^}, L^{^} - ортогональное дополнение к L.
   Лемма 2.  Пусть G открыто в H, g : G ® H есть K-отображение и x₀ О G такая, что l_f(x₀) № 0. Тогда существует содержащаяся в G окрестность V конечного дефекта точки x₀ такая, что g на V есть гомеоморфизм. Следовательно, существует окрестность U Й V в G точки x₀ такая, что g(U) бесконечномерно.
   Теорема 3.  Пусть G открыто в H, X локальное компактное, в частности компактное подмножество из H, и f : G ® H - замкнутое K-отображение. Пусть, далее, для точки x₀ О G существует такая ее окрестность U₀ в G, что f(U₀) М X. Тогда l_f(x₀) = 0.
   Предложение 2.  Пусть M М H множество, допускающее терминальные производные, и X - произвольное подмножество конечномерного линейного подпространства L М H. Пусть, далее, f : M ® H есть K-отображение, а x₀ О M такая точка, у которой существует окрестность U в M такая, что f(U) М X. Тогда l_f(x₀) = 0. В частности, если f(M) М X, то l_f(x₀) = 0 на M.
   Замечание 2.  Важен тот факт, что если множество M М H обладает тем свойством, что для каждой точки x₀ О M любая ее окрестность U в M бесконечномерна, то M является множеством, допускающим терминальные производные.
   Важными примерами множеств M, допускающими терминальные производные, являются каждое из нижеследующих множеств:
   1. бесконечномерные линейные подпространства M М H, открытые и канонически замкнутые в M множества, в частности, бесконечномерные открытые и замкнутые шары;
   2. множество M, для каждой точки x₀ О M которого существует окрестность в M точки x₀, гомеоморфная открытому множеству бесконечномерного линейного подпространства из H, в частности, гильбертовые многообразия M М H, моделью для которых служат бесконечномерные линейные подпространства из H;
   3. гильбертов куб Q и Q-многообразия, т.е. такие подмножества M М H, для которых каждая точка x₀ О M обладает окрестностью в M, гомеоморфной открытому подмножеству из Q. Пусть M - произвольное подмножество H.
   Определение 5.  Скажем, что K₀-отображение f : M ® H обладает K₀-терминальной производной, если терминальные производные l_g(x) всех K₀-продолжений g : G ® H отображения f совпадают между собой на M; получающуюся непрерывную единственную вещественную функцию l_g(x)|M назовем K₀-терминальной производной отображения f и обозначим через l⁰_f(x). Отметим, что если M - множество, допускающее терминальные производные, то для K₀-отображений f : M ® H терминальные производные l_f(x) и l_f⁰(x) совпадают.
   Предложение 3.  Для подмножества M М H рассмотрим условия:
   a₀) для каждой точки x₀ О M, каждой ее окрестности U М M в M, каждого подпространства L М H и каждого числа 0 < d < [(p)/2] существует пара различных точек x,y О U такая, что угол между вектором x - y и подпространством L не меньше [(p)/2] - d;
   b₀) каждое K₀-отображение f : M ® H обладает K₀-терминальной производной;
   c₀) если K₀-отображения g₁ : G₁ ® H и g₂ : G₂ ® H совпадают на M, то на M совпадают и их K₀-терминальные производные. Тогда имеют место импликации: a₀ ® c₀ ® b₀ ® c₀.
   Замечание 3.  Факты, указанные в замечании 1, остаются справедливыми для множеств M, удовлетворяющих условию a₀) предложения 3.
   Определение 6.  Множество M М H, удовлетворяющее условию a₀) предложения 3, будем называть множеством, допускающим K₀-терминальные производные.
   Справедливы аналоги леммы 1, теоремы 1 и 2 и предложения 2, если множество M, допускающее терминальные производные, заменить множеством, допускающим K₀-терминальные производные, K-отображение - K₀-отображением, а l_f(x₀) - на l_f⁰(x₀). В частности имеет место утверждение:
   Предложение 4.  Пусть M М H - множество, допускающее K₀-терминальные производные, f : M ® H - K₀-отображение, X М M - компактное подмножество. Тогда для любого e > 0 существуют открытое в M подмножество U Й X, конечномерное подпространство L М H, число d, 0 < d < [(p)/2], такие, что если точки x,y О U, x № y и угол между вектором x - y и L не меньше [(p)/2] - d, то

|| f(x) - f(y) - l0f(x)(x - y) || Ј e || x - y || .

   3. Множества со свойствами терминальной и K₀-терминальной производной.  Пусть M М H - произвольное подмножество H.
   Определение 7.  Множество M, удовлетворяющее условию c), значит и b), (соотв. c₀), значит и b₀)) (см. предложения 1, 3), будем называть множеством со свойством терминальной (соотв. K₀-терминальной) производной.
   Легко проверить, что если M содержит всюду плотное подмножество M₀ (в частности M = 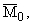удовлетворяющее c) (соотв. c₀), то таким же будет M; объединение любого семейства множеств, удовлетворяющих c) (соотв. c₀), также удовлетворяет c) (соотв. c₀). Наконец если M удовлетворяет c) (соотв. c₀), то таким будет и M × [0,1].
   Отметим, что если M - множество, допускающее терминальные производные, то для него c₀) и c) равносильны.
   Предложение 5.  Пусть M₁ и M₂ - множества со свойством K₀-терминальной производной, а f₁ : M₁ ® M₂, f₂ : M₂ ® H - K₀-отображения. Тогда имеет место

l0f20f1(x) = l0f1(x)l0f2(f1(x))  для x О Mi.

   Предложение 6.  Пусть M - множество со свойством K₀-терминальной производной, f : M ® N сюръективное K₀-отображение, K₀-терминальная производная l⁰_f(x) которого тождественно не равна нулю на прообразе f^-1(y) для каждой точки y О N. Тогда N будет множеством со свойством K₀-терминальной производной.
   Теорема 4. Свойство K₀-терминальной производной является K₀-топологическим инвариантом, т.е. если из K₀-гoмеоморфных множеств одно - множество со свойством K₀-терминальной производной, то и другое будет таким же. При этом если f : M @ N - K₀-гомеоморфизм, то