ГЕОФИЗИКА
УДК 550.837
А. К. Матевосян
Способ обработки результатов площадных электроразведочных
измерений при нерегулярной сети пунктов наблюдений
(Представлено академиком Р. Т. Джрбашяном 7/VIII 2001)
Настоящая статья является логическим
продолжением работы [1], в которой оценена погрешность площадных
электроразведочных исследований (контактным способом регистрации) [2-4],
связанная с точностью установления пунктов наблюдений, и c целью повышения их
эффективности обоснована необходимость разработки методики таких исследований
при нерегулярной сети пунктов наблюдений. В данной работе рассмотрена
возможность использования нерегулярной (произвольной) сети пунктов наблюдений
при площадных электроразведочных исследованиях и на примерах разнотипных
геоэлектрических моделей показана эффективность предлагаемого способа
регистрации и преобразования (трансформации) первичного и вторичного
электрических полей (методами сопротивлений и ВП).
Для осуществления поставленной задачи вычислены основные
интерпретируемые параметры кажущегося сопротивления rS (rSmax,rSmin,rSmed =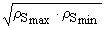 ,
rSrel = rSmax/rSmin,
здесь rSmax,rSmin - главные (экстремальные) значения rS ) и кажущейся поляризуемости hS (аналогично rS) при исследовании методами сопротивлений и
вызванной поляризации многоэлектродной установкой ABCD [5]. Расчеты проведены
при координатах питающих электродов A(-60, -50), B(-30, 70), C(70, -30), D(50,
60) (в метрах) для планшета съемки: -42 м Ј (x,y) Ј 42м, при шаге по x и y
равном 1.5 м, для следующих четырех геоэлектрических моделей:
,
rSrel = rSmax/rSmin,
здесь rSmax,rSmin - главные (экстремальные) значения rS ) и кажущейся поляризуемости hS (аналогично rS) при исследовании методами сопротивлений и
вызванной поляризации многоэлектродной установкой ABCD [5]. Расчеты проведены
при координатах питающих электродов A(-60, -50), B(-30, 70), C(70, -30), D(50,
60) (в метрах) для планшета съемки: -42 м Ј (x,y) Ј 42м, при шаге по x и y
равном 1.5 м, для следующих четырех геоэлектрических моделей:
1- однородная анизотропная
среда, при rn = 1200 Ом·м, rt = 800 Ом·м, hn = 0.01, ht = 0.05, a =
750, b = 400 (здесь rt и rn -
удельное электрическое сопротивление вдоль и поперек плоскости простирания
одноосной анизотропии, ht и hn - поляризуемость при тех же направлениях, a - угол падения плоскости анизотропии, b - угол между простиранием плоскости анизотропии и осью y
против часовой стрелки);
2 - вертикальный контакт двух однородных сред, при r1 = 1000 Ом·м, h1 = 0.01, r2 = 800 Ом·м, h2=0.10;
3 - однородная изотропная среда (r0 = 1000 Ом·м, h0 = 0.01), содержащая полусферическую
неоднородность, при r1 = 800 Ом·м, h1 = 0.10, x1 = 2 м, y1 = 2
м, r = 10 м (здесь x1, y1 - координаты, r - радиус
неоднородности);
4 - однородная
изотропная среда (r0 = 1000 Ом·м,
h0 = 0.01), содержащая сферическое тело, при
r1 = 800 Ом·м, h1 = 0.50, x1 = 2 м,
y1 = 2 м, z1 = 12 м, r = 10 м (здесь
x1, y1, z1 - координаты, r - радиус
тела).
Представим способ преобразования
данных, полученных нерегулярной сетью пунктов наблюдений, в правильную.
Допустим, что определение вектора напряженности электрического поля A в
рассматриваемом пункте N(xN,yN) нерегулярной сети
выполняется по результатам измерений двумя и более (k Ј
2) приемными линиями (каждая из которых представлена двумя приемными
электродами, один из которых распoложен в пункте N, другой - в одном из смежных
пунктов) с разносами, не превышающими R. В результате таких измерений для пункта
N вычисляются (нормируя величину разности потенциалов между электродами по
разносу соответствующей приемной линии) p1-, .., pk-
составляющие вектора A: Ap1(N), ..,
Apk(N). Взяв попарно значения произвольных составляющих
вектора A, можно преобразовать их в требуемые x- и y-составляющие, по
формулам [6]:
|
| Axij(N) = (Api(N)sinnj(N) - Apj(N)sinni(N))/sin(nj(N) - ni(N)), | |
| Ayij(N) = (Api(N)cosni(N) - Apj(N)cosnj(N))/sin(nj(N) - ni(N)), | | |
| |
(1) |
при sin(nj(N) - ni(N)) № 0,
т.е. когда векторы Api(N) и Apj(N)
не коллинеарны (пункты i и j не находятся на одной прямой с N). Здесь
(i,j) = 1,..., k; (i < j); ni(nj) - угол между положительными направлениями осей
x и pi (pj) при отсчете от полярной оси против часовой
стрелки.
Тогда усредненные значения x- и
y-составляющих вектора A в пункте N нерегулярной сети определим из m
Ј k(k - 1)/2 полученных значений
по выражениям:
|
| Ax(N) = |
е
|
(Axij(N) · Wij(N))/ |
е
|
Wij(N)
и Ay(N) = |
е
|
(Ayij(N) · Wij(N))/ |
е
|
Wij(N), | | |
| |
(2) |
где
Wij(N) = (R/di(N)-1)(R/dj(N)-1)
- весовой коэффициент, при R > (di(N),
dj(N)); di(N) = и dj(N) =
и dj(N) =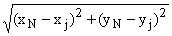 - разнос приемных линий i и j,
соответственно.
- разнос приемных линий i и j,
соответственно.
С использованием (2) получим
усредненные значения x- и y-составляющиx вектора A в пункте
M(xM,yM) правильной сети:
|
| Ax(M) = |
е
|
(Axi(N) · Wi(M))/ |
е
|
Wi(M) и Ay(M) = |
е
|
(Ayi(N) · Wi(M))/ |
е
|
Wi(M), | | |
| |
(3) |
здесь суммирование выполняется для n
(количество смежных с M пунктов нерегулярной сети), при R >
di(M), где di(M) =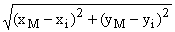 № 0.
№ 0.
При di(M) = 0 составляющим Ax(M) и
Ay(M) присваиваются значения Axi(N)
и Ayi(N), соответственно.
Путем геометрических построений определение x- и y- составляющих вектора
A в пункте N выполняется следующим образом: сперва по значениям
(величинам с учетом знаков) двух произвольных (но не коллинеарных)
pi- и pj-составляющих строится вектор A
(Api(N) и Apj(N) стороны
параллелограмма, |A| - его
диагональ, проходящая через начало координат), а затем, опустив перпендикуляры с
его конца соответственно на оси X и Y, определяются Ax и
Ay. При необходимости можно определить и произвольную составляющую
A. С целью оценки погрешности или визуализации результатов преобразований
(1) можно воспользоваться следующей особенностью: проекции вектора A при
всевозможных осях, проходящих через начало координат, располагаются на
окружности, диаметром которой является данный вектор, а длина хорды, отсекаемой
произвольной осью, равна величине соответствующей его
составляющей.
Следует отметить, что в краевых
частях планшета съемки могут наблюдаться некоторые искажения (уменьшение
точности), ввиду измерения требуемых составляющих напряженности электрического
поля по результатам измерений в определенном направлении (отсутствия равномерно,
всесторонне расположенных смежных пунктов). В этом случае можно рекомендовать
способ линейного интерполирования (и экстраполирования) векторного поля,
предложенный при изучении поля БТ в требуемом полевом пункте по трем базисным
пунктам [7] или же использовать при промежуточных этапах расчетов
соответствующего параметра некоторые процедуры из пакета SURFER, в
частности: Minimum Curvature или Kriging [8]. Очевидно, что
предлагаемые преобразования данных площадной векторной съемки нерегулярной сетью
наблюдений в правильную позволяют полностью применять известные методики
электроразведочных исследований.
Теперь
воспользуемся произвольно заданной нерегулярной разряженной (более чем в 3 раза)
сетью пунктов наблюдений, установленных в пределах вышепредставленного планшета
съемки, фрагмент которой изображен на рис.1,а. Линиями на рис.1,б-г соединены
пункты, расстояние между которыми не превышает R, показывающие, какие
составляющие исследуемого электрического поля привлечены при преобразовании
данных нерегулярной сети в правильную. Величины R выбраны кратными шагу
правильной сети. Заметим, что при R = 3 м (рис.1,б) некоторые пункты соединены со
смежными одной или двумя (почти расположенными на одной прямой) линиями и тем
самым при преобразовании данных в этих пунктах невозможно определение требуемых
значений поля, что в итоге приводит к появлению "белых пятен" на картах
интерпретируемых параметров. С другой стороны, при R = 6 м (рис.1,г) в процессе
преобразования данных для каждого пункта привлекается довольно много смежных
пунктов, более удаленных от рассматриваемого пункта, что приводит как к
существенному увеличению компьютерного времени преобразований, так и в
определенной степени сглаживает поле (аномалии), что может привести к уменьшению
контрастности проявления исследуемых параметров. Для данной нерегулярной сети
оптимальным можно считать R = 4.5 м (рис.2,в).

Рис. 1. Верхний левый фрагмент нерегулярной разряженной
сети пунктов наблюдений (а, б,
в, г) и пункт наблюдений №160 (д) со смежными
пунктами, расположенными в его
окрестности с радиусами R, равными 3, 4.5, 6 м
(линиями соединены пункты, расстояние
между которыми не превышает R, равный 3 м
(б), 4.5 м (в) и 6 м (г); пунктирная квадратная
сетка - правильная сеть
наблюдений).
На рис.1,д крупным планом показан пункт
наблюдений №160 со смежными (тремья, шестью, четырнадцатью) пунктами при этих
радиусах усреднения (приведения) данных R, соответственно. Заметим, что при
преобразовании данных в этих пунктах использование некоторых пар приемных линий,
таких как: №161 и 162; №241 и 246; №128 и 156; №129 и 241; №156 и 247; №128 и
247 - не целесообразно, поскольку они располагаются почти на одной прямой с
пунктом №160, что приводит к увеличению погрешности преобразований. С целью
уменьшения влияния данного фактора на конечный результат при расчетах
принимались во внимание только те пары приемных линий, для которых соблюдалось
условие: |sin(nj(N) - ni(N))| >
0.1 (при экспериментальных исследованиях рекомендуется |sin(nj(N) - ni(N))| і 0.5 [6]).
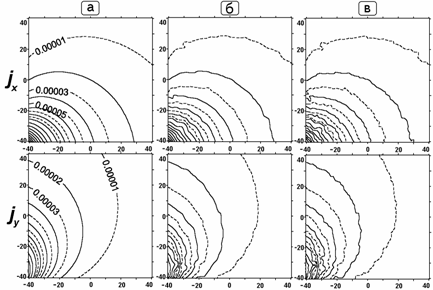
Рис. 2. Карты изолиний x- и y-составляющих вектора j (в
A/м2) при возбуждении
электрического поля током, пропускаемым через
питающий электрод A, по данным: а -
квадратной сети; б, в - нерегулярной
разряженной сети при R, равном 4.5 м (б - в пунктах
нерегулярной сети; в - в
пунктах квадратной сети после соответствующей трансформации).
Наблюдаемая схожесть приведенных карт x- и
y-составляющих вектора j (рис.2,б,в), построенных различными вариантами
по данным нерегулярной разряженной сети, и их несущественные расхождения
("волнистость" изолиний) с исходными картами jx и jy,
соответственно (рис.2,а), несомненно говорит в пользу предлагаемого способа
регистрации и преобразования данных (об устойчивости предлагаемого алгоритма
решения поставленной задачи). Об этом свидетельствует и сопоставление карт
различных параметров кажущегося сопротивления и кажущейся поляризуемости (в
частности rSmed и hSmed при R = 4.5 м в случае нерегулярной сети -
рис.3), несмотря на их общую характерную особенность - незначительную
(несущественную для достижения поставленной цели) "волнистость" изолиний.
Рис. 3. Карты изолиний rSmed (в Ом · м) и hSmed на поверхности четырех (1, 2, 3, 4)
геоэлектрических моделей при возбуждении электрического поля многоэлектродной
системой AD-BC, построенные по данным в пунктах наблюдений: а - правильной сети;
б -
нерегулярной сети; в - нерегулярной сети после трансформации в
рассматриваемую
правильную сеть.
 В заключение следует отметить, что применение
нерегулярной сети пунктов наблюдений требует проведения дополнительных
топографических полевых работ, связанных с определением координат каждого пункта
(приемного электрода). Можно также рекомендовать применение современных
зарубежных многоканальных (сотни и даже тысяча каналов) электроразведочных
станций, однако целесообразна разработка многофункциональной измерительной
компьютеризированной аппаратуры с соответствующим программным обеспечением,
позволяющей проводить комплексные электроразведочные исследования методами с
контактным способoм измерений.
В заключение следует отметить, что применение
нерегулярной сети пунктов наблюдений требует проведения дополнительных
топографических полевых работ, связанных с определением координат каждого пункта
(приемного электрода). Можно также рекомендовать применение современных
зарубежных многоканальных (сотни и даже тысяча каналов) электроразведочных
станций, однако целесообразна разработка многофункциональной измерительной
компьютеризированной аппаратуры с соответствующим программным обеспечением,
позволяющей проводить комплексные электроразведочные исследования методами с
контактным способoм измерений.
Институт геологических наук НАН РА
Литература
1. Матевосян А. К. - - ДНАН РА. 2002. T.101. №2. C.
2.
Инструкция по электроразведке. Л. Недра. 1984. 352
с.
3. Электроразведка.
Справочник геофизика (под ред. В. К. Хмелевского и В. М. Бондаренко). М. Недра.
1989. В 2-х кн. 438 с., 378 с.
4. Комаров В. А. - Электроразведка методом вызванной
поляризации. Л. Недра. 1980. 391 с.
5. Матевосян А. К. - Изв. НАН РА. Науки о Земле. 1999. Т.52.
№1. С. 53-63.
6. Матевосян А.
К. - Изв. НАН РА. Науки о Земле. 1999. Т.52. №2-3. С. 84-88.
7. Матевосян А. К. Способ геоэлектроразведки. Авторское свидетельство СССР №1704120.
Бюллетень изобретений №1. 1992.
8. SURFER for WINDOWS. Contouring and 3D Surface Mapping. Version 6. User’s
Guide. Golden Software. 1997.


