ТЕОРИЯ УПРУГОСТИ

УДК 539.3

А. С. Погосян

О Колебаниях проводящих пластин в поперечном магнитном поле

(Представленно академиком В.С. Саркисяном 18/VI 2002)

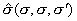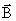   Пусть трансверсально-изотропная упругая пластинка постоянной толщины 2h, изготовленная из материала с конечной электропроводностью колеблется во внешнем магнитном поле с постоянным вектором магнитной индукции (0,0,B3), нормальным к срединной плоскости пластинки. Прямоугольная система координат xyz выбрана так, что координатная плоскость xoy совпадает со срединной плоскостью, к которой параллельна плоскость изотропии. Принимается что сторонние токи и заряды отсутствуют, электромагнитные свойства, среды окружающей пластинку, эквивалентны свойствам вакуума и что магнитная проницаемость m = 1. При этом, предполагая, что электромагнитное поле в пластинке во времени изменяется не слишком быстро, пренебрегаем токами смещения по сравнению с токами проводимости.
   Принимая гипотезу уточненной теории изгиба пластин [1], из уравнений движения пластинки с учетом сил электромагнитного происхождения [2] будем иметь следующие уравнения:
D DDW+2rh ж
з
и 		1 - h2
3
 D - 2Eh2
5Gў(1-u2)
 D + 2rh2
5Gў
 2
t2
 ц
ч
ш 		2W
t2
 =
= - sB3
c2
t
 h
у
х
-h 
 h3zdz + 2shB32
c2
 ж
з
и 		h2
3
 D - 2rh2
5Gў
 2
t2
 ц
ч
ш 		W
t
 ,
 (1)
DF - 5Gў
2Gh2
 F - r
G
 2F
t2
 = - 5Gў
2Gh2
 sB3
c
 й
к
л 		3
2h3
 h
у
х
-h 
 ж
з
и 		e1
x
 + e2
y
 ц
ч
ш 		zdz - B3
c
 2h2
5Gў
 F
t
 щ
ъ
ы 		,
 (2)

   где D = [(2Eh2)/(3(1 - v2))] - жесткость пластинки; G = [E/(2(1 + v))] - модуль сдвига в плоскости изотропии; Gў - модуль сдвига для плоскостей, перпендикулярных плоскости изотропии; F = [(¶F)/(y)] - [(¶Y)/(x)]; F,Y - функции, характеризирующие поперечные сдвиговые деформации пластинки.
   К этим уравнениям следует присоединить линеаризованные уравнения электродинамики как во внутренней, так и во внешней областях пластинки [2,3], со следующими условиями на поверхностях (z = ±h):

ei = ei(e),    hi = hi(e),    h3 = h3(e)   (i = 1,2)
 (3)
и условием на бесконечности
hi,ei ® 0,    (i = 1,2,3)  при  z ® ±Ґ.
 (4)
   Рассматривая решения типа гармонических волн
{W,F} = { W0,F0}ei(wt-k1x-k2y),   W0,F0 = const,
{ei.hi} = {ei0(z),hi0(z)}ei(wt-k1x-k2y),    (i = 1,2,3),
 (5)
из вышеперечисленных уравнений и соотношений будем иметь:
   для определения частоты поперечных колебаний согласно (1)
Dr4 - 2rhw2 ж
з
и 		1 + h2r2
3
 + 2Eh2r2
5Gў(1-u)
 - 2rh2
5Gў
 w2 ц
ч
ш 		=
= - 2shB32iw
c2
 h2r2
3
 й
к
л 		1 - 4psiw
c2c2
 ж
з
и 		1 - d(1+rh)
chchch+rhshch
 ц
ч
ш 		щ
ъ
ы 		+
 (6)
+ 2shB32iw
c2
 2rh2
5Gў
 w2 й
к
л 		1 - 4psiw
c2c2
 ж
з
и 		1 - 5
c2h2
 ж
з
и 		1 - d(1 + rh(1 - h2c2/3))
chchch + rhshch
 ц
ч
ш 		ц
ч
ш 		щ
ъ
ы 		.
   Если не учитывать поперечные сдвиговые деформации Gў ® Ґ,r2h2 << 1, то из (6) получим
Dr4 - 2rhw2 = - 2shB32iw
c2
 h2r2
3
 й
к
л 		1 - 4psiw
c2c2
 ж
з
и 		1 - d(1 + rh)
chchch + rhshch
 ц
ч
ш 		щ
ъ
ы 		,
 (7)
что совпадает с выражениями полученными в [3,4];
   для определения частоты сдвиговых колебаний согласно (2)
w2 - 5Gў
2rh2
 ж
з
и 		1 + 2h2r2
5
 G
Gў
 ц
ч
ш 		=
= sB32iw
c2
 й
к
л 		1 + 5
2c2h2
 ж
з
и 		1 - 4psc0h + iwc2h2
ch(4psc0hchch + iwchshch)
 ц
ч
ш 		щ
ъ
ы 		.
 (8)
   Здесь c2 = r2 + [(4psiw)/(c2)], c02 = r2 - [(w2)/(c2)], d = [(3(chchch - shch))/(c2h2)], r2 = ki2 + k22, для простоты принято sў = s.
   Разлагая соответствующие функции в асимптотический ряд по параметру |c|h и пренебрегая членами порядка |c|3h3 по сравнению с единицей
|c|3h3 << 1,
 (9)
для определения частоты поперечных колебаний из (6) получим
Dr4 - 2rhw2 ж
з
и 		1 + h2r2
3
 + 2Eh2r2
5Gў(1 - u)
 - 2rh2
5Gў
 w2 ц
ч
ш 		=
=  - 2shB32iw
c2
 й
к
л 		h2r2
3
 ж
з
и 		1 - 2
5
 4psiwh2
c2(1 + rh + c2h2/2)
   ц
ч
ш 		-
 (10)
= - 2rh2
5Gў
 w2 ж
з
и 		1 - 2
5
 4psiw
c2c2(1 + rh + c2h2/2)
 ц
ч
ш 		щ
ъ
ы 		,
из (7) получим
Dr4 - 2rhw2  = - 2shB32iw
c2
 h2r2
3
 й
к
л 		1 - 2
5
 4psiwh2
c2(1 + rh + c2h2/2)
 щ
ъ
ы 		.
 (11)

   Исходя из того, что пренебрежение токами смещения означает выполнение условия 4ps >> |iw| и принимая более слабое условие 4psrh >> |iwc2|h2 для частот, характеризующих сдвиговые колебания пластинки, получим (в приближении (9))

й
к
л 		w2 - 5Gў
2rh2
 ж
з
и 		1 + 2h2r2
5
 G
Gў
 ц
ч
ш 		щ
ъ
ы 		ж
з
и 		1 + h2c2
2
 ц
ч
ш 		= sB23iw
rc2
 .
 (12)

   Отметим, что (10), (11) и (12) получены без принятия каких-либо гипотез относительно компонент электромагнитного поля.
   Принимая линейный закон изменения компонент электромагнитного поля [5]

e1 = j + zj1,    e2 = y + zy1,    h3 = f + zf1,
 (13)
   из уравнений (1), (2) и уравнений электродинамики во внутренней области получим [6]
D DDW + 2rh ж
з
и 		1 - h2
3
 D - 2Eh2
5Gў(1 - u2)
 D + 2rh2
5Gў
 2
t2
 ц
ч
ш 		2W
t2
 =
= - 2h3
3
 sB3
c2
 f1
t
 + 2sh B32
c2
 ж
з
и 		h2
3
 D - 2rh2
5Gў
 2
t2
 ц
ч
ш 		W
t
ж
з
и 		1 - h2
3
 D + 4ps
c2
 h2
3
t
 ц
ч
ш 		f1 +
x
 ж
з
и 		h1+ + h1-
2
 ц
ч
ш 		+
y
 ж
з
и 		h2+ + h2-
2
 ц
ч
ш 		=
= - 4psB3
c2
 ж
з
и 		h2
3
 D - 2rh2
5Gў
 2
t2
 ц
ч
ш 		W
t
 ,
 (14)
DF - 5Gў
2Gh2
 F - r
G
 2 F
t2
 = - 5Gў
2Gh2
 sB3
c
 й
к
л 		g1 - B3
c
 2h2
5Gў
 F
t
 щ
ъ
ы
g1 + c
4psў
 ж
з
и 		D - 4psў
c2
t
 ц
ч
ш 		й
к
л 		H+ - 4ps
c2
 h2
3
 ж
з
и 		g1 - B3
c
 2h2
5Gў
 F
t
 ц
ч
ш 		щ
ъ
ы 		= 0,
 (15)
где g1 = [(j1)/(x)] + [(y1)/(y)], H+ = [()/(y)]([(h1+ + h1-)/2h]) - [()/(x)]([(h2+ + h2-)/2h]).

   К этим уравнениям также следует присоединить уравнения электродинамики во внешней области с условиями (3),(4).
   Представляя искомые функции в виде (5), из перечисленных уравнений и соотношений для величин hi0+ + hi0-  (i = 1,2) получим
h10+ + h10-
2h
 =- iw
cc0
 y10 + ik1
c0
 f10,     h20+ + h20-
2h
 = iw
cc0
 j10 + ik2
c0
 f10.
 (16)
   Если же относительно характера изменения компонент электромагнитного поля в окружающей среде принять дополнительное допущение [2,3], то получим выражения [6]
[¯](h1+ + h1-) = 2h
l
 ж
з
и 		f1
x
 + 1
c
 y1
t
 ц
ч
ш 		,    [¯](h2+ + h2-) = 2h
l
 ж
з
и 		f1
x
 - 1
c
 j1
t
 ц
ч
ш 		,
 (17)
где [¯] є [(2)/(x2)] + [(2)/(y2)] -  [1/(c2)][(2)/(t2)].
   Откуда с помощью (5) получим
h10+ + h10-
2h
 = - iw
clc02
 y10 + ik1
lc02
 f10,     h20+ + h20-
2h
 = iw
clc02
 j10 + ik2
lc02
 f10.
 (18)
   Сравнивая (16) и (18), замечаем, что выражения для hi0+ + hi0- совпадут, если за характерный размер принять l = c0-1 (в случае w2c-2 << r2, l = r-1).
   Согласно (14,15,17) задачи определения величин W,f1 и F,j1,y1 распадаются:
D DDW + 2rh ж
з
и 		1 - h2
3
 D - 2Eh2
5Gў(1 - u2)
 D + 2rh2
5Gў
 2
t2
 ц
ч
ш 		2W
t2
 =
= - 2h3
3
 sB3
c2
 f1
t
 + 2sh B32
c2
 ж
з
и 		h2
3
 D - 2rh2
5Gў
 2
t2
 ц
ч
ш 		W
t
 ,
[¯] й
к
л 		ж
з
и 		1 + h
l
 - h2
3
 D + 4ps
c2
 h2
3
t
 ц
ч
ш 		f1 + 4psB3
c2
 ж
з
и 		h2
3
 D - 2rh2
5Gў
 2
t2
 ц
ч
ш 		W
t
 щ
ъ
ы 		= 0;
 (19)
DF - 5Gў
2Gh2
 F - r
G
 2 F
t2
 = - 5Gў
2Gh2
 sB3
c
 й
к
л 		g1 - B3
c
 2h2
5Gў
 F
t
 щ
ъ
ы 		,
g1 + c
4psў
 ж
з
и 		D - 4psў
c2
t
 ц
ч
ш 		й
к
л 		H+ - 4ps
c2
 h2
3
 ж
з
и 		g1 - B3
c
 2h2
5Gў
 F
t
 ц
ч
ш 		щ
ъ
ы 		= 0,
[¯] H+ = - 1
lc
 g1
t
 .
 (20)
   Представляя искомые функции в виде (5), из (19) и (20) получим
Dr4 - 2rhw2 ж
з
и 		1 - h2r2
3
 + 2Eh2r2
5Gў(1 - u2)
 - 2rh2
5Gў
 w2 ц
ч
ш 		=
= - 2shB32iw
c2
 ж
з
и 		h2r2
3
 - 2rh2
5Gў
 w2 ц
ч
ш 		й
к
л 		1 - 4psiwh2
3c2(1+ rh + c2h2/3)
 щ
ъ
ы
(21)
й
к
л 		w2 - 5Gў
2rh2
 ж
з
и 		1 + 2h2r2
5
 G
Gў
 ц
ч
ш 		щ
ъ
ы 		ж
з
и 		1 + h2c2
3
 ц
ч
ш 		= sB32iw
rc2
 .
 (22)
   Если в (21) не учитывать поперечные сдвиговые деформации то имеем
Dr4 - 2rhw2 = - 2shB32iw
c2
 h2r2
3
 й
к
л 		1 - 4psiwh2
3c2(1 + rh + c2h2/3)
 щ
ъ
ы 		.
 (23)

   Сравнивая (11) с (23) и (12) с (22), замечаем, что они почти совпадают, т.е. линейный закон изменения компонент e1,e2,h3 в этих задачах соответствует приближению |c|3h3 << 1.
   Отметим, что задача поперечных колебаний электропроводящей пластинки в поперечном магнитном поле в рамках классической теории пластин исследованa в работах [3,4] - показано, что точность гипотезы магнитоупругости тонких тел соответствует приближению |c|2h2 << 1.
   В работе [7], принимая уточненную теорию пластин и применяя операторный метод в комплексе с методом усреднения для компонент индуцированного электромагнитного поля e1,e2,h3, получен кубический закон изменения. Пренебрегая инерцией вращения, обусловленной учетом поперечных деформаций, для определения относительной частоты поперечных колебаний шарнирно опертой по краям пластинки полосы (шириной а) получено следующее характеристическое уравнение:

ж
з
и 		2b0h* + n0H*
3d3
 ц
ч
ш 		W3 + H*W2 + ж
з
и 		2b0 + n0
3d3
 ц
ч
ш 		W + 1 = 0,
 (24)
W = w
w0
 ,    w0 =   ж
 ъ
Ц
E
3r(1 - n2)
 
 hl2m,    lm = mp
a
 , h* = 2Eh2l2m
5Gў(1 - u2)
 ,    n0 = 4psw0h2
c2
 ,    
H* = 1 + h* + h2l2m
3
 ,    d3 = 5(l + h)
6l + h
 + l2mh2
3
 .

   На основе уточненной теории пластин и линейного закона изменения компонент e1,e2,h3 (уравнения (14)), в работе [6] для аналогичной задачи получено характеристическое уравнение

ж
з
и 		2b0h* + n0H*
3d1
 ц
ч
ш 		W3 + H*W2 + ж
з
и 		2b0 + n0
3d1
 ц
ч
ш 		W + 1 = 0,
 (25)
d1 = 1 + hlm + h2l2m
3
 .

   Сравнивая (24) с (25), замечаем, что они отличаются лишь коэффициентом di   (1,3), при этом (в (1.9) принимая l = lm-1) d3 = d1 - [(lmh(1 + lmh))/(6 + lmh)].
   Таким образом, уравнение (24) (полученное с помощью линейного закона (13)) и уравнение (25) (полученное с помощью операторного метода) качественно аналогичны.
    В заключение выражаю глубокую благодарность проф. С. В. Саркисяну за ценные советы и постоянное внимание к работе.
   Ереванский государственный университет

 

Литература

   1. Амбарцумян С. А. Теория анизотропных пластин. М. Наука. 1987. 360 с.
   2. Амбарцумян С. А., Багдасарян Г. Е., Белубекян М. В. Магнитоупругость тонких оболочек и пластин. М. Наука. 1977. 272 с.
   3. Амбарцумян С. А., Белубекян М. В. Колебания и устойчивость токонесущих пластин. Изд. АН Армении, Ереван. 1992. 123 с.
   4. Мкртчян П. А. - Изв. АН АрмССР. 1983. T. 36. N6. C. 39-49.
   5. Амбарцумян С. А., Багдасарян Г. Е. Электропроводящие пластинки и оболочки в магнитном поле. М. Наука. 1996. 286 с.
   6. Саркисян С. В., Погосян А. С. Изв. НАН Армении. Механика. 2000. T.53. N1. C. 59-65.
   7. Саркисян В. С., Саркисян С. В., Джилавян С. А., Саргсян А. Л. - Механика. Межвуз. сб. науч. трудов, Вып.8. Ереван. ЕГУ. 1991. C. 49-60.