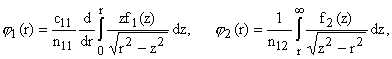ТЕОРИЯ УПРУГОСТИ
УДК 539.3
В. С. Тоноян, С. А. Мелкумян
Контактная задача для ортотропной полуплоскости с
вертикальными
соосными конечными и полубесконечными разрезами
(Представлено академиком Б. Л. Абрамяном 28/ IX
2001)
В работе рассматривается плоская контактная
задача для упругой ортотропной полуплоскости (x і 0,
|z| < Ґ) с вертикальными соосными конечным (0 < x < b) и
полубесконечным (c < x < Ґ) разрезами. На
конечном участке границы (|z|
Ј a) полуплоскости приложен жесткий штамп с основанием
произвольной гладкой формы, симметрично расположенный относительно оси разрезов
(z = 0). Предполагается, что трение между штампом и полуплоскостью отсутствует.
Для простоты принимается также, что на границе полуплоскости вне штампа (|z| > a) и конечном разрезе (0
< x < b) действует только нормальное давление.
Рассматривается плоское деформированное состояние (
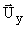 = 0,
[(¶[
= 0,
[(¶[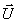 ])/(¶y)] = 0), и задача
решается в перемещениях методом Фурье. Решение представлено в виде суперпозиции
решений а) симметричной и б) кососимметричной задачи относительно оси разрезов
(z = 0). Решение каждой из этих задач представлено в виде сумм интегралов Фурье.
Поиск произвольных функций интегрирования в каждой задаче в конечном счете
сводится к решению системы из парных и тройных интегральных уравнений, которое в
свою очередь сводится к решению интегральных уравнений типа Фредгольма второго
рода. Показана разрешимость последних для конкретного ортотропного
материала.
])/(¶y)] = 0), и задача
решается в перемещениях методом Фурье. Решение представлено в виде суперпозиции
решений а) симметричной и б) кососимметричной задачи относительно оси разрезов
(z = 0). Решение каждой из этих задач представлено в виде сумм интегралов Фурье.
Поиск произвольных функций интегрирования в каждой задаче в конечном счете
сводится к решению системы из парных и тройных интегральных уравнений, которое в
свою очередь сводится к решению интегральных уравнений типа Фредгольма второго
рода. Показана разрешимость последних для конкретного ортотропного
материала.
а. Рассматривается симметричная
контактная задача для упругой ортотропной полуплоскости с вертикальными соосными
конечным и полубесконечным разрезами. Так как задача симметрична относительно
оси z = 0, то можно ограничиться рассмотрением только правого квадранта (0 < x
< Ґ, 0 < z < Ґ).
Граничные условия для квадранта имеют вид:
|
| tzx(0, z) = 0 (0 < z <
Ґ), tzx(x, 0) = 0 (0
< x < Ґ), | | |
| |
(1) |
|
| Ux(0,
z) = f1(z) (0 < z Ј
a), sx(0,
z) = f2(z) (a < z < Ґ), | | |
| |
(2) |
|
| sz(x, 0) = f3(x)
(0 < x < b), Uz(x, 0) = 0 (b
Ј x Ј
c), sz(x,
0) = 0 (c < x < Ґ). | | |
| |
(3) |
Решение задачи ищем в виде сумм
интегралов Фурье:
|
| C11Ux(x,z) = |
Ґ
у
х
0
|
a |
U
|
(a,
z)sinaxda + |
Ґ
у
х
0
|
b |
U
|
*
|
(b,x)cosbzda, | |
| C44Uz(x,z) = |
Ґ
у
х
0
|
a |
W
|
(a,z)cosaxda + |
Ґ
у
х
0
|
b |
W
|
*
|
(b,x)cosbzdb. | | |
| |
(4) |
Плотности интегралов Фурье (4),
затухающие в глубь полуплоскости, определяются в виде:
|
|
U
|
(a,z) = |
2
е
j=1
|
D1(tj)Aj(a)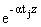 , , |
U
|
*
|
(b,
x) = |
2
е
k=1
|
D1(tk)t-2kBk(b)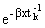 , , | |
|
W
|
(a,z) = |
2
е
j=1
|
D2(tj)Aj(a)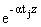 , ,
|
W
|
*
|
(b,
x) = |
2
е
k=1
|
D2(tk)Bk(b)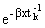 . . | | |
| |
(5) |
Здесь Aj(a) и Bk(b) - неизвестные
функции интегрирования, которые определяются из граничных условий (1)-(3), а
D1(tk) и D2(tk) - по формулам:
|
| D1(tk) = |
ж
з
и
|
|
c13
c44
|
+ 1 |
ц
ч
ш
|
tk,
D2(tk) = 1- |
c44
c11
|
tk2, | | |
| |
(6) |
где tk определяется из
решения следующего биквадратного уравнения (причем Retk > 0 ):
|
|
c33
c11
|
t4 + |
ж
з
и
|
|
c132
c44c11
|
+ 2 |
c13
c11
|
- |
c33
c44
|
|
ц
ч
ш
|
t2 + 1 = 0. | | |
| |
(7) |
Здесь c11,
c13, c33, c44- модули упругости ортотропного
материала.
Используя основные соотношения
теории упругости [1] для исследуемой среды и (4), (5), можно все компоненты
тензора напряжений выразить через Aj(a) и
Bk(b).
Удовлетворяя граничным условиям (1), получаем [2]:
|
| Aj(a) = ajAj(a) + |
2
p
|
|
Pj
a12
|
|
1
a
|
|
2
е
k=1
|
b1kbktk2 |
Ґ
у
х
0
|
|
b2B1(b)
b2 + a2tk2
|
dB, | | |
| |
(9) |
где
|
| b1 = 1 b2 = - |
b11
b12
|
,
a1 = 1,
P1 = 0, a2 = - |
a11
a12
|
,
P2 = 1, | |
| bik = |
c44
c11
|
|
D1(tk)
tk2
|
- |
D2(tk)
tk
|
,
aij |
c44
c11
|
D1(tj)tj + D2(tj). | | |
| |
(10) |
Имея в виду (8) и удовлетворяя смешанным граничным условиям (2),
получаем следующие парные интегральные уравнения:
|
м
п
п
п
н
п
п
п
о
|
|
Ґ
у
х
0
|
bB1(b)sinbzdb = |
c11
n11
|
f1(z) (0
< z Ј a),
(11) | |
|
Ґ
у
х
0
|
b2B1(b)sinbzdb = - |
1
n12
|
f2(z) + |
1
n12
|
|
2
е
j=1
|
a2j |
Ґ
у
х
0
|
a2Aj(a)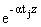 da (a < z < Ґ), da (a < z < Ґ), | | |
| |
где
|
| n11 = |
2
е
k=1
|
D1(tk)tk-2bk,
n12 = |
2
е
k=1
|
b2kbk,
| |
| b2k = D1(tk)tk-3 + |
c13
c44
|
D2(tk),
a2j = D1(tj) - |
c13
c44
|
D2(tj)tj.
| | |
| |
(12) |
Удовлетворяя смешанным граничным
условиям (3) и имея в виду соотношения (8), (9), получаем следующие тройные
интегральные уравнения [2]:
|
м
п
п
п
п
н
п
п
п
п
о
|
|
|
Ґ
у
х
0
|
a2A(a)cosaxda =
f3(x) (0 < x <
b), | |
|
Ґ
у
х
0
|
aA(a)cosaxda = f(x)
(b Ј x Ј c),
(13) | |
|
Ґ
у
х
0
|
a2A(a)cosd xda =
0 (c < x < Ґ), | | |
| |
где
|
| A(a) = a31A1(a) + a32A2(a), | | |
| |
(14) |
|
| f(x) = |
2
е
k=1
|
b*1kbk |
Ґ
у
х
0
|
bB1(b)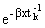 db, db, | | |
| |
(15) |
| a3j = |
c13
c11
|
D1(tj) - |
c33
c44
|
D2(tj)tj,
b*1k= |
2
p
|
mb1ktk - D2(tk), m = |
D2(t1)a32 - D2(t2)a31
D2(t1)a12 - D2(t2)aa11
|
. | |
(16) |
Из соотношений (9) и (14) можно
получить
|
| Aj(a) = a*jA(a) + |
2
p
|
|
Pj*
a
|
|
2
е
k=1
|
b1kbktk2 |
Ґ
у
х
0
|
|
b2B1(b)
b2 + a2tk2
|
db; | | |
| |
(17) |
здесь
|
| aj*= |
a12
a31a12 - a32a11
|
,
Pj*= |
Pj
a12
|
- |
a31aj
a31a12 - a32a11
|
. | | |
| |
(18) |
Решение поставленной задачи сведено к решению систем из парных (11) и
тройных (13) интегральных уравнений, имея в виду также интегральное соотношение
(17).
Подобные парные интегральные уравнения
рассматривались в работах [3-5]. Используя результаты работы [5], решая (11)
методом преобразующих операторов для неизвестной функции B1(b), получаем следующее соотношение:
|
| B1(b) = |
2
p
|
|
1
b
|
|
Ґ
у
х
0
|
j1(r)J0(br)dr + |
2
p
|
|
1
b
|
|
Ґ
у
х
a
|
rj2(r)J0(br)dr + |
2
p
|
|
1
b
|
|
Ґ
у
х
a
|
rF(r)J0(br)dr, | | |
| |
(19) |
где
|
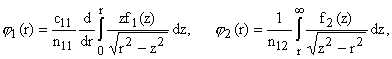
|
(20) |
|
| F(r) = |
1
n12
|
|
2
е
j=1
|
a21 |
Ґ
у
х
0
|
a2Aj(a)K0(atjr)da, | | |
| |
(21) |
J0(br) - функция Бесселя первого рода с действительным
аргументом,
Ki(ar) - функция
Макдональда.
Тройные интегральные уравнения,
подобные (13), рассматривались в работах [6-9].
Следуя [9], из (13) получаем:
|
| A(a) = |
1
a
|
|
Ґ
е
n=0
|
An*J2k+1(ca), | | |
| |
(22) |
|
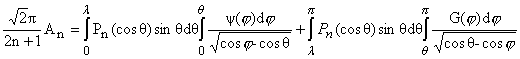
|
(23) |
где
|
| An(2n + 1) = (-1)An*,
y(j) = |
2
е
k=1
|
b1k*bktk |
Ґ
у
х
0
|
bB1(b) |
ж
з
и
|
1 - e-[(bc)/(tk)]cosj/2 |
ц
ч
ш
|
db, | | |
| |
(24) |
| G(j) = |
p
у
х
j
|
g(j)dj + c1, g(j) = - |
c
2
|
|
ccosj/2
у
х
q
|
f3(ccosj/2)sin(j/2)dj, c1
= |
Ґ
е
n=1
|
(-1)nAn, | |
Pny
- полином Лежандра.
Имея в виду (17), (21), (23), (24), исключая A(a) из (19) и (22), для определения B(b) =
bB1(b) получаем следующее интегральное уравнение типа Фредгольма
второго рода:
|
| B(b) =
W(b) + |
Ґ
у
х
0
|
K(g,b)B(g)dg, | | |
| |
(25) |
где
|
| W(b) = |
2
p
|
|
a
у
х
0
|
j1(r)J0(br)dr + |
2
p
|
|
Ґ
у
х
0
|
rj2(r)J0(br)dr + | |
| + |
2
p
|
|
1
n12
|
|
2
е
j=1
|
a2jaj* |
Ґ
у
х
a
|
rJ0(br)dr |
Ґ
у
х
0
|
a2w1(a)K0(atjr)da, | | |
| |
(26) |
|
| K(b,g)
= |
2
p
|
|
1
n12
|
|
2
е
j=1
|
a2jaj* |
Ґ
у
х
a
|
rJ0(br)dr |
Ґ
у
х
0
|
a2w1(a,g)K0(atjr)da + | |
| + |
4
p2
|
|
g
n12
|
|
2
е
j=1
|
a2jPj* |
2
е
k=1
|
b1kbkt2k |
Ґ
у
х
a
|
rJ0(br)dr |
Ґ
у
х
0
|
|
aK0(atjr)
g2 + a2t2k
|
da; | | |
| |
(27) |
здесь
|
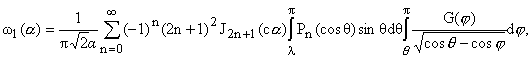 |
| w2(a) = |
1
p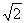 a a
|
|
2
е
k=1
|
b1k*bktk |
Ґ
е
n=0
|
(-1)n(2n
+ 1)2J2n+1(ca) |
l
у
х
0
|
Pn(cosq)sinqdq× (28) | |
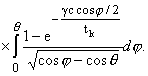 | |
| |
Очевидно, что функция
W(b) ограничена сверху и
стремится к нулю, когда b ® Ґ.
Используя значения интегралов [2]:
|
Ґ
у
х
0
|
rK0(ar)J0(br)dr = |
1
a2 + b2
|
, |
Ґ
у
х
0
|
r2K1(ar)J0(br)dr = |
2a
(a2 + b2)2
|
| |
и
результатов [9], можно показать разрешимость уравнений (25) для каждого
конкретного ортотропного материала.
Решая
уравнения (25) определим B(b) = bB1(b), а потом можно по
формулам (24), (23), (22), (17) и (8) определить все искомые функции и,
следовательно, напряжения и перемещения в любой точке
полуплоскости.
б. Рассматривается
кососимметричная контактная задача для упругой ортотропной полуплоскости с
вертикальными соосными конечным и полубесконечным
разрезами.
В этом случае граничные условия
для правого квадранта имеют вид:
|
| tzx(0,z) = 0 (0
< z < Ґ),
sz(x,0) = 0 (0
< x < Ґ), | |
| Ux(0,z) = f4(z) (0
< z Ј a),
sx(0,z) = f5(z) (a
< z < Ґ), | |
| txz(x,0) = 0 (0
< x < b, c < x < Ґ),
Ux(x,0) = 0 (b
Ј x Ј
c). | | |
| |
(29) |
Решение задачи ищем в виде:
|
| c11Ux(x,z) = |
Ґ
у
х
0
|
a |
U
|
(a,z)sinaxda + |
Ґ
у
х
0
|
b |
U*
|
(b,x)cosbzdb, | |
| c44Uz(x,z) = |
Ґ
у
х
0
|
a |
W
|
(a,z)cosaxda + |
Ґ
у
х
0
|
b |
W*
|
(b,x)sinbzdb | | |
| |
(30) |
Плотности интегралов Фурье (30) определяются по формулам
(5).
Удовлетворяя граничным условиям (29),
получаем следующие системы из парных и тройных интегральных уравнений:
|
м
п
п
п
п
н
п
п
п
п
о
|
|
Ґ
у
х
0
|
bB1(b)cosbzdb = |
c11
n11
|
f1(z) (0
Ј z Ј
a), | |
|
|
|
Ґ
у
х
0
|
b2B1(b)cosbzdb = - |
1
n12
|
f2(z) + |
1
n12
|
|
2
е
j=1
|
a2j |
Ґ
у
х
0
|
a2Aj(a)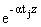 da (a < z < Ґ), da (a < z < Ґ), | | |
| |
|
м
п
п
п
п
п
н
п
п
п
п
п
о
|
|
Ґ
у
х
0
|
a2[a11A1(a) + a12A2(a)]sinaxda =
0 (0 < x < b, c < x < Ґ), | |
|
|
|
Ґ
у
х
0
|
a[D1(t1)A1(a) + D1(t2)A2(a)]sinaxda =
| |
| = - |
2
е
k=1
|
D1(tk)tk-2bk |
Ґ
у
х
0
|
bB1(b)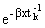 db (b Ј x Ј
c) db (b Ј x Ј
c) | | |
| |
и
интегральные соотношения
|
| Aj(a) = ajA1(a) - |
2
p
|
|
Pj
a32
|
|
1
a2
|
|
2
е
k=1
|
b3kbktk |
Ґ
у
х
0
|
|
b3B1(b)
b2 + a2tk2
|
db, | | |
| |
(33) |
а также зависимость (8), где
|
| b3k = - |
c13
c11
|
|
D1(tk)
tk3
|
+ |
c33
c44
|
D2(tk). | | |
| |
(34) |
Решая (31) методом преобразующих
операторов [10], получим
|
| B1(b) = |
2
p
|
|
1
b
|
|
a
у
х
0
|
j3(r)J1(br)dr + |
2
p
|
|
1
b
|
|
Ґ
у
х
a
|
j4(r)J1(br)dr + |
2
p
|
|
1
b
|
|
Ґ
у
х
a
|
F1(r)J1(br)dr; | | |
| |
(35) |
здесь
|
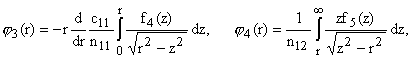 |
| F1(r) = - |
r
n12
|
|
2
е
j=1
|
a2j |
Ґ
у
х
0
|
a2Aj(a)K1(atjr)da. | | |
| |
(36) |
После
некоторых простейших преобразований (32)
можно привести к виду [2]:
|
м
п
п
п
н
п
п
п
о |
|
Ґ
у
х
0
|
a2A(a)sinaxda = 0
(0 < x < b, c < x <
Ґ), | |
|
|
|
Ґ
у
х
0
|
aA(a)sinaxda =
f*(x) (b Ј x Ј
c), | | |
| |
где
|
| A(a) = a11A1(a) + a12A2(a),
m1 = |
D1(t1)a12 - D1(t2)a11
D1(t1)a32 - D1(t2)a31
|
| |
| b*3k = m1b3ktk - D1(tk)tk-2, | |
| f*(x) = - m1 |
2
е
k=1
|
b3kbktk |
Ґ
у
х
0
|
bB1(b)db + |
2
е
k=1
|
b*3kbk |
Ґ
у
х
0
|
bB1(b)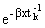 db. db. | | |
| |
(38) |
Используя результат работы [11], из (37) получаем
|
| A(a) = |
1
a2
|
|
Ґ
у
х
0
|
w(a,b)bB1(b)db, | | |
| |
(39) |
где
|
| w(a,b) = |
1
p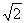
|
|
2
е
k=1
|
bk |
Ґ
е
n=0
|
(-1)n(2n +1 )2J2n+1(ca) |
l
у
х
0
|
Pn(cosq)sinqdq× | |
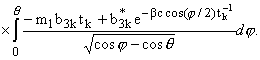 | |
| |
(40) |
Используя соотношения (39), (38) и (33), можно получить выражение
|
| Aj(a) = |
1
a2
|
|
a32
a11a32 - a12a31
|
aj |
Ґ
у
х
0
|
w(a,b)bB1(b)db + | |
| + |
2
p
|
|
1
a2
|
|
ж
з
и
|
|
a12
a11a32 - a12a31
|
aj - |
Pj
a32
|
|
ц
ч
ш
|
|
2
е
k=1
|
b3kbktk |
Ґ
у
х
0
|
|
b3B1(b)
b2 + a2t2k
|
db. | | |
| |
(41) |
Имея в виду (36), исключая Aj(a) из
(35) и (41), для определения B(b) = bB1(b) получим
интегральные уравнения типа Фредгольма второго рода
(25).
Свободные члены и ядро интегрального
уравнения выражаются следующими формулами:
|
| W(b) = |
2
p
|
|
a
у
х
0
|
j3(r)J1(br)dr + |
2
p
|
|
Ґ
у
х
a
|
j4(r)J1(br)dr, | | |
| |
(42) |
|
| K(b,g) = - |
2
p
|
|
1
n12
|
|
2
е
j=1
|
a2j |
Ґ
у
х
a
|
rJ1(br)dr |
Ґ
у
х
0
|
|
й
к
л
|
|
a32aj
a11a32 - a12a31
|
w(a, g) + | |
| + |
2
p
|
Pj** |
2
е
k=1
|
b3kbktk |
g2
g2 + a2tk2
|
|
щ
ъ
ы
|
K1(atjr)da, | | |
| |
(43) |
здесь
Pj** = [(a12)/(a11a32-a12a31)] - [(Pj)/(a32)]
Разрешимость полученных интегральных
уравнений доказывается аналогично первому пункту. После определения
B1(b), используя (41) и (8), определяются
также все искомые функции. Потом, используя основные соотношения теории
упругости [1], можно определить напряжения и перемещения в любой точке
полуплоскости.
Институт механики НАН РА
Литература
1. Крестенсен Р. Введение в
механику конпозитов. М. Мир. 1982. 337 c.
2. Градштейн И. С., Рыжик И. М. Таблицы интегралов, сумм,
рядов и произведений. Наука. 1971. 1100c. М.
3. Баблоян А. А. - ПММ. 1964. Т. 28. вып. 6.
4. Sneddon I. N. - Proc.
Glasqou Math Ass. 1960. V. 4. P. 108-110.
5. Тоноян В. С. - Изв. АН АрмССР. Механика. 1968. T. 21. N.
3. C. 3-18.
6. Tranter G. I. - Proc. Glasqou Math Ass. 1960. V. 4. Pt.. 4. P.
200-212.
7. Валов Г. М. - Изв.
АН СССР. МТТ. 1972. N 5.
8. Баблоян А. А.,
Мхитарян С. М. -Изв. АН АрмССР. Механика. 1969. Т. 22. N 6.
9. Тоноян В. С. - ДАН АрмССР.
1963. Т. 37. N5. C. 249-258.
10. Тоноян В.
С., Мелкумян С. А. -ДАН АрмССР. 1970. T. 51. N 3. C. 144-149.
11. Тоноян В. С. - ДАН АрмССР.
1963. T. 37. N 3. C. 121-130.