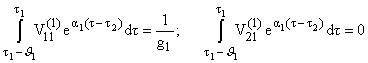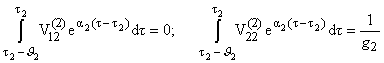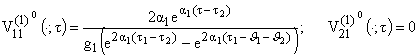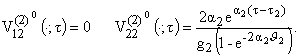УДК 62.50

   Рассматривается линейная система дифференциальных уравнений, и ставится задача оптимального наблюдения при наличии потока информации. Предполагается, что в различные промежутки времени наблюдаются различные сигналы из этого потока. Строится оптимальный фильтр, восстанавливающий фазовый вектор в конечный момент времени наблюдения.
   1. Пусть имеется система

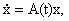(1.1)

где x О Rⁿ, A(t) - n × n матрица с измеримыми и ограниченными элементами на промежутке t О [t₀, T]. Предполагается, что наблюдается идеальный сигнал

y(t) = м п п н п п о y(1)(t),  при  t О [t1-J1, t1] y(2)(t),  при  t О [t2-J2, t2] -----------------------------                                        (1.2) y(k)(t),  при  t О [tk-Jk, tk],

где t₀ Ј t₁-J₁, t_i Ј t_i+1-J_i+1, J_i > 0, (i = 1,..., k-1), t_k < T.
   Предполагается также, что

y(i)(t) = Gi(t) x(t),     t О [ti-Ji,ti],

(1.3)

где сигнал y⁽ⁱ⁾(t)-(m_i×1) - мерный, а G_i(t)-(m_i×n) - мерная матрица, элементы которой непрерывные функции при t О [t_i-J_i,t_i].
   Если сигналы y⁽ⁱ⁾(t) (1.3) продолжить нулями при t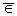[t_i - J_i,t_i], то (1.2) можно записать в следующем глобальном виде:

y(t) = G(t)x(t).

   2. Сформулируем следующую задачу наблюдения [1, 2].
   Требуется определить линейные операции, удовлетворяющие следующим условиям:

jj[t1,...,tk;y(t)] = xj(tk)   (j = 1,...,n)

или в векторном виде

j[t1,...,tk;y(t)] = x(tk).

   Целесообразно указанную линейную операцию искать в виде

tk у х t1-u1  V(t1,...,tk;t)y(t)dt = x(tk).

(2.1)

   Здесь матрица

V(t1,...,tk;t) = (V(1)(t1,t),...,V(k)(tk,t))

(2.2)

имеет размерность (n×).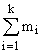

   Используя формулу Коши для решения системы (1.1), получим

x(t) = X[t,ti],x(ti)    (i = 1,...,k),

(2.3)

где X[t,t_i] - нормированная фундаментальная матрица системы (1.1). Подставляя значение x(t) из (2.3) в (1.3) и учитывая (1.2), из (2.2) получим

tk у х t1-J1  k е i=1  V(i)(ti,t)Gi(t)X[t,tk]x(tk)dt = x(tk).

(2.4)

   Так как вектор x(t_k) может принимать любое значение из Rⁿ, то из (2.4) следует, что

tk у х t1-J1  k е i=1  V(i)(ti,t)Gi(t)X[t,tk]dt = E,

(2.5)

где E - единичная матрица.
   В литературе [1-3] условия (2.5) называются интегральными условиями. Известно, что не всегда существует матрица V(·), удовлетворяющая условиям (2.5). Если предполагать, что функция V(·), удовлетворяющая условиям (2.5), существует (которая в общем случае не является единственной), то эту функцию можно определить при помощи проблемы моментов при минимизации соответствующего функционала.
   а) При минимизации функционала

tk у х t1-J1  V2(t1,...,tk;t)dt = tk у х t1-J1  k е i=1  mi е s=1  n е p=1  (Vps(i)(·,t))2dt

(2.6)

с условиями (2.5) определение оптимального фильтра можно привести к изопериметрической задаче [1].
   б) При минимизации функционала

sup t1-J1 Ј t Ј tk  k е i=1  mi е s=1  n е p=1  |Vps(i)(·,t)|

с условиями (2.5) оптимальный фильтр можно определить при помощи проблемы моментов [1] и т.д.
   Таким образом, когда минимизируемый функционал удовлетворяет условиям нормы, поставленная задача наблюдения решается при помощи проблемы моментов.
   Замечание. Часто на каждом этапе наблюдения получаемый сигнал не является полным, но в совокупности при помощи полученной информации вида (1.2) полностью определяется состояние фазового вектора. Следует отметить, что во многих практических задачах эффективный процесс наблюдения происходит вышеуказанным образом.
   3. Рассмотрим конкретный пример.

. x   = a1x1,     . x   = a2x2.

Здесь a₁ = const, a₂ = const
   Пусть поступающий сигнал имеет вид

y(t) = м п н п о y(1)(t) = g1x1(t),  при  t О [t1-J1, t1]; y(2)(t) = g2x2(t),  при  t О [t2-J2, t2];  t1 Ј t2-J2,

где g₁ = const, g₂ = const.
   Интегральные условия для этой задачи будут

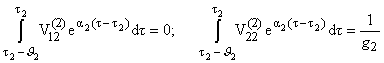(3.1)

   

Пусть минимизируется функционал:

t1 у х t1-J1  [(V11(1)(·, t))2 + (V21(1)(·, t))2]dt + t2 у х t2-J2  [(V12(2)(·, t))2 + (V22(2)(·, t))2]dt

(3.2)

   Если рассматривать задачу (3.1), (3.2) как изопериметрическую, то ее решением будет

   Таким образом, оптимальный фильтр в данном случае будет иметь следующий вид:
   Следует отметить, что на каждом отдельном этапе наблюдения указанная система не вполне наблюдаема.

   Ереванский государственный университет

Литература

   1. Красовский Н. Н. Теория управления движением. М. Наука. 1968. 476с.
   2. Куржанский А. Б. Управление и наблюдение в условиях неопределенности. М. Наука. 1977. 392 с.
   3. Гантмахер Ф. Р., Крейн М. Г. Осцилляционные матрицы и ядра и малые колебания механических систем. М. Гостехиздат. 1950. 359 с.

---