Из
определения (2)-(4) непосредственно следует, что
| ||u||p Ј ||u||p* Ј ||u||p,a | |
(5) |
для всех p > 0 и a > 1, и неравенства считаются формальным в случае
бесконечности какой-либо из величин (2)-(4). С другой стороны, классическая
максимальная теорема Харди-Литтквуда [7] утверждает, что для аналитической
функции f в круге U условие ||f||p < +Ґ для всех p
> 0 равносильно свойству ||f||p* < +Ґ.
Если функция u(z) гармоническая в U, то, согласно основной теореме статьи [8],
для любых p > 0 и a > 1 можно указать такую
универсальную положительную постоянную Ap,a,
что
и неравенство считается формальным,
если правая часть бесконечна.
Гармоническую
в круге U функцию u(z) относят к малому классу Харди hp, p > 0,
если ||u||p < +Ґ. Аналитическую в круге U функцию f(z) относят к большому
классу Харди Hp, p > 0, если ||f||p < +Ґ, а последнее
равносильно тому, что u,v О hp, p > 0,
где f(z) = u(z) + iv(z), z О U, (см. [1,
§1.1])
Определение 1. Гармоническую функцию u(z),
определенную в круге U, отнесем к классу
hpmax, p > 0, если ||u||p* < +Ґ,
так что вложение hpmax Н
hp справедливо для всех p > 0.
Нетрудно доказать также, исходя из определения (3), строгие вложения
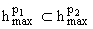 для всех 0 < p2 <
p1.
для всех 0 < p2 <
p1.
Замечание 1. Отмеченная выше максимальная теорема Харди-Литтлвуда показывает, что
необходимость введения максимального аналога
 , p >
0, для класса hp, p > 0, отпадает, поскольку
, p >
0, для класса hp, p > 0, отпадает, поскольку
 = Hp, p > 0.
= Hp, p > 0.
Теорема 1.
Функция u(z) принадлежит классу
hpmax, p > 0, в том и только в том случае, когда она
представима в виде u(z) = Re f(z) для некоторой функции f(z) класса Hp,
p > 0. При этом, если функция f в этом представлении нормированна условием Im
f(0) = 0, то
с некоторой постоянной
Cp > 0, не зависящей от u
Замечание 2. В частном случае p = 1 этот результат
сформулирован и доказан в [2] (гл. VIII, §D, п.2). Похожий результат для
функции, определенных в полуплоскости, отмечен в [9] (§, теорема 9 и следствие
2).
Доказательство. Согласно определения 1, функция (3), (4) и неравенства (5) и (6),
функция
u(z)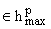 ,
p > 0 тогда и только тогда, когда ||u||p,a < +Ґ для p > 0 и всех
a > 0. Для гармонической функции u(z) в круге U
существует единсвенная с точностью до аддитивной постоянной сопряженная
гармоническая функция v(z), такая что функция u(z) +
iv(z) = f(z) голоморфна в U.
Если функцию v(z) нормировать условием v(0) =
0, то в силу основного результата
статьи [5] получим неравенство
,
p > 0 тогда и только тогда, когда ||u||p,a < +Ґ для p > 0 и всех
a > 0. Для гармонической функции u(z) в круге U
существует единсвенная с точностью до аддитивной постоянной сопряженная
гармоническая функция v(z), такая что функция u(z) +
iv(z) = f(z) голоморфна в U.
Если функцию v(z) нормировать условием v(0) =
0, то в силу основного результата
статьи [5] получим неравенство
справедливое для всех p > 0 и
a > 1 с некоторой постоянной Cp,a > 0, не зависящей от u(z) и v(z). Поэтому, с учетом
изложенного в начале доказательства утверждения, заключаем, что ||f||p < +Ґ и u(z)
= Re f(z), z О U, для функции f О
Hp, p > 0. Неравенство (7) следует из неравенства (8) подстановкой
в него неравенства (6).
Следствие 1.
Для любого p > 0 существует
конечная постоянная Cp > 0 такая, что
| |u(z)| Ј Cp |
ж
з
и |
|
1 +
|z|
1 - |z|
|
|
ц
ч
ш |
1/p
|
||u||p*, z О U, | |
(9) |
для любой функции u(z) О
 , p >
0.
, p >
0.
Доказательство. По
теореме1 для любой функции u(z) О
 , p > 0, найдем голоморфную функцию f О Hp, p > 0, удовлитворяющую оценке (7) с
постоянной Cp > 0, не зависящей от u(z) такую, что u
= Re f. Известная оценка модуля функции класса Hp (см., например, [4] гл. II,
§3, п. 1) имеет вид
, p > 0, найдем голоморфную функцию f О Hp, p > 0, удовлитворяющую оценке (7) с
постоянной Cp > 0, не зависящей от u(z) такую, что u
= Re f. Известная оценка модуля функции класса Hp (см., например, [4] гл. II,
§3, п. 1) имеет вид
| |f(z)| Ј |
ж
з
и |
|
1 + |z|
1 - |z|
|
|
ц
ч
ш |
1/p
|
||f||p, z О U, | |
(10) |
с учетом неравенства |u(z)| Ј
|f(z)| и оценки (7), получаем
(9).
Другое следствие теоремы 1 связана с
понятием углового предела функции u(z) в граничной точке eiq. Так называют значение w
О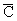 , которое является
пределом функции u(z), когда z стремится к eiq, оставаясь в каждой области Da(q), a > 1, одним и тем же для всех Da(q), a > 1, и которое обозначается w =
u(eiq).
, которое является
пределом функции u(z), когда z стремится к eiq, оставаясь в каждой области Da(q), a > 1, одним и тем же для всех Da(q), a > 1, и которое обозначается w =
u(eiq).
Следствие 1.
Произвольная функция u(z) класса
hpmax, обладает конечным угловым пределом u(eiq) для почти всех точек eiq О
T.
Доказательство. Согласно теореме 1, любая функция u О
hpmax, p > 0, имеет представление u
= Re f, f О Hp, p > 0. Так как функция классов
Hp, p > 0, обладают конечными угловыми пределами почти всюду на T
(см., например, [4]), то утверждение следствия 2 справедливо на основании
непрерывности операции взятия действительной части комплексного
числа.
Замечание 3. Выше отмечалось, что функция классов hp, p > 0, являются
действительными частями функции классов Hp, p > 0, так что
утверждение теоремы 1 и следствий 1 и 2 доставляют новую информацию только в
случае 0 < p Ј 1.
2. Соотношения между классами hp
и hpmax, p > 0. Согласно упомянутой
в начале статьи теореме М. Рисса, при любом p > 1 условия ||u||p < +Ґ и ||v||p < +Ґ для любой пары
сопряженных гармонических в U функций u(z) и v(z) равносильны. Так как при этом
функция f(z) = u(z)
+ iv(z) принадлежит классу Hp, p > 1, то по
максимальной теореме Харди-Литтлвуда [7] имеем ||u||p* < +Ґ.
Таким образом, при p > 1 классы hp и hpmax
совпадают (как множества функций). Это утверждение становится неверным уже при
p = 1, как показывает пример функции (1). Справедлива, однако,
следующая
Теорема 2. Любая функция u(z) класса h1,
а также ее сопряженная функция
v(z), принадлежит каждому из классов hpmax, 0 < p <
1. Если, дополнительно, функция v(z) нормирована условием v(0)
= 0, то
неравенства
| ||u||p* Ј Kp||u||1, ||v||p* Ј Kp||u||1 | |
(11) |
справедливы с некоторой конечной
постоянной Kp, зависящей только от p, 0 < p <
1.
Доказательство. Известная теорема Колмогорова (см., например, [2], гл.V, §D, п.5)
утверждает, что для любой гармонической функции u(z), представимой в круге U
интервалом Пуассона-Лебега, голоморфная функция f(z) =
u(z) + iv(z) принадлежит
классам Hp для любого p, 0 < p < 1, где v(z) - сопряженная к
u(z) функция с v(0) =
0; при этом ||f||p Ј Lp||u||1 с
конечной постоянной Lp > 0,
зависящей только от p. В статье [10], (с. 29) отмечено, что утверждение теоремы
Колмогорова остается справедливым для произвольной функции u класса
h1, поскольку в ее доказательстве интеграл Пуассона-Лебега можно
заменить интегралом Пуассона-Стилтьеса. Согласно максимальной теореме
Харди-Литтлвуда, имеет оценку ||f||p* Ј
Dp||f||p с постоянной
Dp > 0, зависящей толско от p. Объединяя обе оценки и учитывая
неравенства |u(z)| Ј |f(z)|,
|v(z)| Ј |f(z)|, z
О U, получаем (11) с
Kp = Lp·Dp.
В
заключении отметим, что в [11] рассматривались некоторые классы
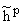 , 0 < p Ј 1, промежуточныв
между
, 0 < p Ј 1, промежуточныв
между
 и hp.
и hp.
3. Топологические свойства классов hpmax, p >
0. Стандартной техникой проверяется, что вводимая формулой
(3) числовая характеристика ||u||p* определяет в классах
hpmax, p > 0, инвариантную метрику
rp*(u1,u2) = (||u1 - u2||p*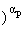 ,
u1,u2 О ,
u1,u2 О , p > 0, ap = min(1, p), , p > 0, ap = min(1, p), | |
преврашающую
каждый класс hpmax, p > 0 в метрическое пространство
(удовлетворение функции rp*
аксиомам метрики непосредственно следует из неравенства треугольника в
пространствах Lp(-p,p), p >
0).
Отметим, что метрику в классах
hpmax можно ввести также посредством угловой числовой
характеристики (4) ввиде
rp,a(u1,u2) = ||u1 - u2||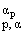 ,
u1,u2 О ,
u1,u2 О
 , p > 0. ap = min(1, p). , p > 0. ap = min(1, p). | |
Однако,
в силу неравенства (6), метрики rp и
Pp,a для любого a
> 1 эквивaлентны по Липшицу, а значит, они топологически эквивалентны и
задают одинаковые равномерные и липшицевы структуры.
Так как, по определению, гармоничекая функция u(z), z О U, принадлежит классу hpmax, p >
0, тогда и только тогда, когда ||u||p* = rp*(u,0) < +Ґ, то из неравенства треугольника для метрики rp* и свойства абсолютной однородности
характеристики ||·||p* следует,
что метрические пространства hpmax, p > 0, замкнуты
относительно операций поточечного сложения функций и умножения функций на
действительное число. Таким образом, классы hpmax, p >
0, образуют линейно-метрическое пространства над полем действительных чисел,
т.е. такие линейные и одновременно метрические пространства, в которых линейные
опреции непрерывны относительно метрик.
Рассматривая классы Hp, p > 0, как метричекие
пространства с естественными метриками rp(f,g) = ||f - g||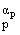 , f,g О
Hp, ap = min(1,p), докажем
следующий результат.
, f,g О
Hp, ap = min(1,p), докажем
следующий результат.
Теорема 3. Для люого p > 0
пространства hpmax изоморфно
некоторому замкнутому линейному подпространству пространства Харди
Hp, p > 0, и следовательно, представляет собой F-пространство
(B-пространство при p і 1) относительно метрики rp* (относительно нормы ||·||p* при p і
1), и сходимость в метрике rp*
сильнее равномерной сходимости на компактах круга
U,
Замечание 4. Как и замечание 3, отметим, что новую информацию теорема 3 доставляет
только в случае 0 < p Ј 1.
Доказательство. Согласно теореме 1, каждой функции u О
 , p > 0, можно поставить в соответствие однозначно
определенную функцию f О Hp, p > 0, с
условием Im f(0) = 0. Обозначим множество таких функций через
H0p, заметим, что в силу оценки (7) для ||f||p и ||u||p*, это соответствие непрерывно. Так
как, по максимальной теореме Харди-Литтлвуда, справедлива и обратная оценка
||u||p* Ј Dp||f||p, то пространство
, p > 0, можно поставить в соответствие однозначно
определенную функцию f О Hp, p > 0, с
условием Im f(0) = 0. Обозначим множество таких функций через
H0p, заметим, что в силу оценки (7) для ||f||p и ||u||p*, это соответствие непрерывно. Так
как, по максимальной теореме Харди-Литтлвуда, справедлива и обратная оценка
||u||p* Ј Dp||f||p, то пространство
 в
действительности изоморфно (в линейном и топологическом смыслах) подпространству
H0p пространства Hp, что доказывает первое
утверждение теоремы 3. Учитывая, что пространство Hp, p > 0 (а,
следовательно, и любое его замкнутое линейное подпространство) является
F-пространством (B-пространством при p і 1)
относительно метрики rp (нормы ||·||p при p і 1), приходим
ко второму утверждению теоремы 3. Утверждение о равномерной сходимости следует из
определения метрики rp* и оценки
(9) в следствии 1.
в
действительности изоморфно (в линейном и топологическом смыслах) подпространству
H0p пространства Hp, что доказывает первое
утверждение теоремы 3. Учитывая, что пространство Hp, p > 0 (а,
следовательно, и любое его замкнутое линейное подпространство) является
F-пространством (B-пространством при p і 1)
относительно метрики rp (нормы ||·||p при p і 1), приходим
ко второму утверждению теоремы 3. Утверждение о равномерной сходимости следует из
определения метрики rp* и оценки
(9) в следствии 1.
Приводимую ниже теорему
можно считать аналогом для пространств
 , p > 0,
исвестной теоремы Ф. Рисса о граничной сходимости в среднем функции пространств
Hp (см., например, [4], гл.II, §4, п.1).
, p > 0,
исвестной теоремы Ф. Рисса о граничной сходимости в среднем функции пространств
Hp (см., например, [4], гл.II, §4, п.1).
Тоерема 4.
Для любой функции u О
 , p > 0,
функции
ur, o Ј r < 1, определяемые формулой
ur(z) = u(rz), z О U, 0 Ј r < 1, сходятся при r®1- к исходной функции u в метрике rp*.
, p > 0,
функции
ur, o Ј r < 1, определяемые формулой
ur(z) = u(rz), z О U, 0 Ј r < 1, сходятся при r®1- к исходной функции u в метрике rp*.
Доказательство. Пусть u О
 , p > 0. Согласно теореме 1, существует такая
аналитическая функция f класса Hp, p > 0, что u
= Re f. Так как для
любой функции f О Hp, p > 0, справедлива
теорема Ф. Рисса (см. [4], гл.II, §4, п.1), то ||fr
- f||p®0 при r®1-, где fr, 0 Ј r < 1,
определены как fr(z) = f(rz), z О U. Тогда для
ur = Re fr, 0 Ј r < 1, на
основании максимальной теоремы Харди-Литтлвуда, имеем ||ur - u||p* Ј ||fr - f||p* Ј
Dp||fr -
f||p®0 при r®1-, т.е. функции ur, o Ј r
< 1, сходятся к функции u при r®1- в метрике rp*.
, p > 0. Согласно теореме 1, существует такая
аналитическая функция f класса Hp, p > 0, что u
= Re f. Так как для
любой функции f О Hp, p > 0, справедлива
теорема Ф. Рисса (см. [4], гл.II, §4, п.1), то ||fr
- f||p®0 при r®1-, где fr, 0 Ј r < 1,
определены как fr(z) = f(rz), z О U. Тогда для
ur = Re fr, 0 Ј r < 1, на
основании максимальной теоремы Харди-Литтлвуда, имеем ||ur - u||p* Ј ||fr - f||p* Ј
Dp||fr -
f||p®0 при r®1-, т.е. функции ur, o Ј r
< 1, сходятся к функции u при r®1- в метрике rp*.
Следствие 4.
Гармонические полиномы двух переменных
плотны в пространствах
 , p > 0
и F-пространства
, p > 0
и F-пространства
 , p > 0, -
сепарабельны.
, p > 0, -
сепарабельны.
Доказательство. Рассмотрим произвольную функцию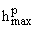 , p > 0, и произвольное число e > 0, и докажем сначала существование гармонического
полинома P(z) = P(x,y), который приближает функцию u в метрике rp* с точностью, не превосходящей e. Опираясь на теорему 1, находим функцию f О Hp, p > 0, у которой Re f
= u. Так как
алгебраические многочлены комплексного переменного плотны в Hp, p
> 0, то для числа e > 0 существует такой
алгебраический многочлен Q(z), что ||f
- Q||p Ј e/Dp, где Dp- положительная постоянная
в оценке ||u||p* Ј Dp||f||p, f О Hp,
u = Re f, p > 0, по максимальной теореме Харде-Литтлвуда. Поэтому ||u - ReQ||p* Ј
Dp||f - Q||p Ј e и P = ReQ - искомый полином, что доказывает первое
утверждение следствия 3. Второе его утверждение, с учетом теоремы 3, является
прямым следствием известных утверждений о том, что произвольный гармонический
полином равномерно на замыкании
, p > 0, и произвольное число e > 0, и докажем сначала существование гармонического
полинома P(z) = P(x,y), который приближает функцию u в метрике rp* с точностью, не превосходящей e. Опираясь на теорему 1, находим функцию f О Hp, p > 0, у которой Re f
= u. Так как
алгебраические многочлены комплексного переменного плотны в Hp, p
> 0, то для числа e > 0 существует такой
алгебраический многочлен Q(z), что ||f
- Q||p Ј e/Dp, где Dp- положительная постоянная
в оценке ||u||p* Ј Dp||f||p, f О Hp,
u = Re f, p > 0, по максимальной теореме Харде-Литтлвуда. Поэтому ||u - ReQ||p* Ј
Dp||f - Q||p Ј e и P = ReQ - искомый полином, что доказывает первое
утверждение следствия 3. Второе его утверждение, с учетом теоремы 3, является
прямым следствием известных утверждений о том, что произвольный гармонический
полином равномерно на замыкании (а значит, и в
метрике пространства
(а значит, и в
метрике пространства
 , p > 0) приближается
гармоническими многочленами с рациональными коэффициентами, множество которых
счетно.
, p > 0) приближается
гармоническими многочленами с рациональными коэффициентами, множество которых
счетно.
Замечание 5. Аналог теоремы 4 для пространств hp, p > 0, не имеет места
уже при p = 1, как показывает пример функции (1); при p
= 1 несправедлив также
аналог следствия 3. Однако положение воссранавливается при p > 1, в силу
отмеченной выше эквиваленстности характеристик ||·||p и ||·||p*.
Московский Государственный Университет им. М.
Ломоносова
Ереванский Государственный
Инженерный Университет