Целью настоящей работы являлся поиск
упрощенного метода расчета токов в листе и контуров их замыкания для
математической обработки электромагнитных преобразователей, доступный для
инженеров-проектировщиков. При этом полученное решение лишь немного отличалось
от точного.
Рис. 1
Одним из методов расчета токов в проводящем
листе, движущемся со скоростью V, является сеточный метод. Суть его состоит в
том, что область проводящего изотропного листа, расположенного в воздушном
зазоре преобразователя, представляется в виде прямоугольника
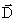 = {0 Ј x Ј M, 0 Ј y Ј N}. Разобьем отрезки [O, M] и [O, N] соответственно на
N1 и N2 части (рис.1). Пусть
hx = [M/(N1)] hy = [N/(N2)].
= {0 Ј x Ј M, 0 Ј y Ј N}. Разобьем отрезки [O, M] и [O, N] соответственно на
N1 и N2 части (рис.1). Пусть
hx = [M/(N1)] hy = [N/(N2)].
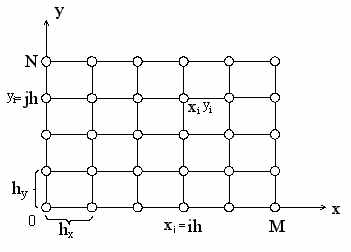
Через точки деления проведем прямые,
параллельные соответствующим осям. В результате пересечения этих прямых получим
узлы (xi,yi), которые и образуют сетку. Расстояние между
соседними узлами xi - xi-1 = hx = [1/(N1)] и
yi - yi-1 = hy = [1/(N2)] назовем шагами
сетки по направлениям x и y соответственно. Так как зона контроля
преобразователя имеет квадратную площадь, то целесообразно применять постоянный
шаг по каждому из направлений, т. е. равномерную сетку.
Каждая сетка является схемой замещения
проводящего листа с идентичной площадью. Поэтому ветви схемы замещения одинаковы
и содержат последовательно соединенные активные сопротивление и индуктивность. В
схеме замещения емкостный элемент отсутствует, так как токи смещения в
проводящем листе в расчет не берутся.
|

|
Рис. 2
Выбранная схема замещения обоснована
экспериментально путем измерения вносимых сопротивлений эталонных образцов
листов различной толщины. Осуществим расчет токов в ветвях сетки при OM = ON = 3a,
N1 = N2 = 12, hx = hy = [3a/12], при этом
ветви сетки представлены как равные комплексные сопротивления.
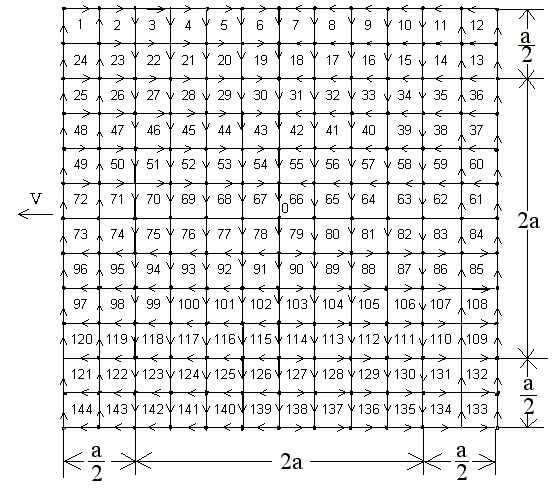
В результате получим сетку, показанную на
рис.2, которая состоит из 144 контуров. С целью упрощения схемы комплексные
сопротивления ветвей не показаны. Приведенная сетка, кроме рабочей площади
2a×2a, находящейся под полюсным наконечником преобразoвателя, содержит участок,
со всех сторон расширенный на величину [a/2]. Это делается для уточнения
контуров замыкания токов в проводящем листе при его движении со скоростью V.
Предполагается, что индукция под полюсным
наконечником площадью 2a×2a однородна и изменяется по синусоидальному закону, а
в расширенном участке отсутствует. Эти допущения делаются исходя из
конструктивных особенностей электромагнитного преобразователя броневой
конструкции [2].
При перемещении сетки, показанной на рис.2,
со скоростью V происходит изменение потокосцепления и в сетке возникает два вида
ЭДС: трансформаторная
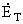 и движения
и движения
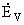 . Для
определения ЭДС трансформации воспользуемся уравнением электромагнитной индукции
. Для
определения ЭДС трансформации воспользуемся уравнением электромагнитной индукции
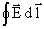 = -[(dF)/dt] Максвелла для шести замкнутных контуров с центром O
(рис.2). Результаты расчетов приведены в таблице.
= -[(dF)/dt] Максвелла для шести замкнутных контуров с центром O
(рис.2). Результаты расчетов приведены в таблице.
Номера контуров от
центра O
|
1 |
2 |
3 |
4 |
5 |
6 |
| ЭДС контуров |
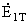 |
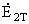 |
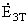 |
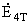 |
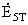 |
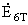 |
Величина ЭДС контура в
относительных
единицах |
1 - j1 |
4 - j4 |
9 - j9 |
16 - j16 |
16 - j16 |
16 - j16 |
Величина ЭДС ветвей
контура в относительных
единицах |
0,125 -j0,125 |
0,25 -j0,25 |
0,375 -j0,375 |
0,5 -
j0,5 |
0,4 -
j0,4 |
0,333333 -
j0,333333
|
Направление ЭДС выбирается исходя из правила
проходного винта. В ветвях сеток, находящихся под полюсными наконечниками
(площадь 2a×2a), поперечеными направлению движения V, возникают ЭДС движения
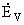 ,
в то время как в ветвях, продольных направлению движения, они не возникают.
Так как длины ветвей сеток одинаковы, а магнитная индукция в рассматриваемом
участке однородна, то
,
в то время как в ветвях, продольных направлению движения, они не возникают.
Так как длины ветвей сеток одинаковы, а магнитная индукция в рассматриваемом
участке однородна, то
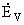 этих ветвей равны
между собой. Их направление выбирается на основании правила правой руки. Здесь принято
этих ветвей равны
между собой. Их направление выбирается на основании правила правой руки. Здесь принято
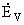 = 1 в относительных единицах. При составлении схемы
замещения сетки, показанной на рис.2, учтены направления
= 1 в относительных единицах. При составлении схемы
замещения сетки, показанной на рис.2, учтены направления
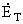 и
и
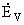 .
.
Определим токи в ветвях сетки на основании
метода наложения.
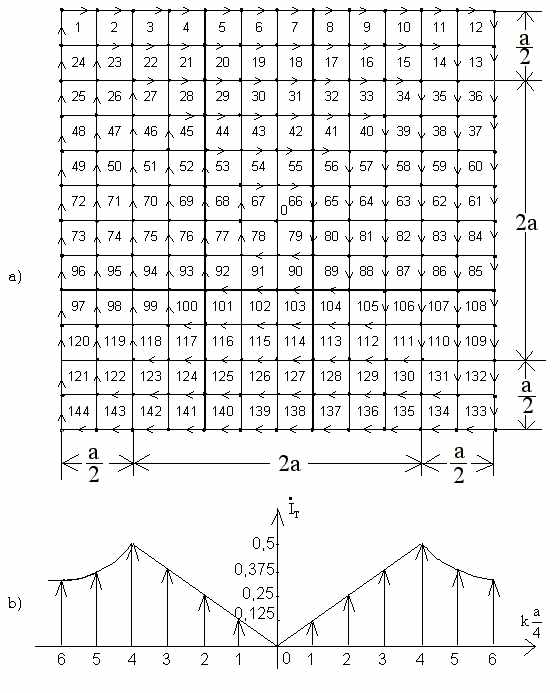
Рис. 3
Вначале найдем токи в ветвях сетки от ЭДС
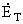 .
Расчетную схему получим из рис. 2, учитывая, что
.
Расчетную схему получим из рис. 2, учитывая, что
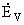 = 0.
Комплексные сопротивления отдельных ветвей сетки одинаковы и принимаются равными
Z0 = r0 + jwL0 = l + jl
относительных единиц.
= 0.
Комплексные сопротивления отдельных ветвей сетки одинаковы и принимаются равными
Z0 = r0 + jwL0 = l + jl
относительных единиц.
Для полученной схемы из 144 контуров
составлены уравнения по контурным токам. Совместное их решение позволило
получить токи в ветвях и закономерности распределения токов трансформаторного
составляющего
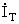 контуров от центра к краям рассматриваемого
участка k[a/4] (где k = 1, 2, 3, 4, 5, 6 номера контуров рис. 3а, в).
контуров от центра к краям рассматриваемого
участка k[a/4] (где k = 1, 2, 3, 4, 5, 6 номера контуров рис. 3а, в).
Теперь определим составляющие токов в ветвях
сетки, обусловленныe
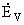 . Расчетную схему также получим из рис.
2, учитывая, что
. Расчетную схему также получим из рис.
2, учитывая, что
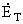 = 0. Комплексные сопротивления ветвей
исходной схемы заменяются активными сопротивлениями и приняты равными
Z0 = r0 = 1 относительных единиц.
Рис. 4
= 0. Комплексные сопротивления ветвей
исходной схемы заменяются активными сопротивлениями и приняты равными
Z0 = r0 = 1 относительных единиц.
Рис. 4
Для полученной схемы из 144 контуров
составлены уравнения по контурным токам. Совместное их решение позволило
получить токи в ветвях, направления которых показаны на рис.4.
Определена магнитная индукция как для
отдельных составляющих токов, так и для их алгебраической суммы. Установлена
результирующая индукция в воздушном зазоре преобразователя.
Государственный инженерный университет
Армении
Литература
1. Шимони К. Теоретическая электротехника. М. Мир. 1964. 773
с.
2. Патент РФ N 1249313 Нерсисиян В. Б. - Открытия. Изобретения. 1986. N
20.
![]() = {0 Ј x Ј M, 0 Ј y Ј N}. Разобьем отрезки [O, M] и [O, N] соответственно на
N1 и N2 части (рис.1). Пусть
hx = [M/(N1)] hy = [N/(N2)].
= {0 Ј x Ј M, 0 Ј y Ј N}. Разобьем отрезки [O, M] и [O, N] соответственно на
N1 и N2 части (рис.1). Пусть
hx = [M/(N1)] hy = [N/(N2)]. ![]() и движения
и движения
![]() . Для
определения ЭДС трансформации воспользуемся уравнением электромагнитной индукции
. Для
определения ЭДС трансформации воспользуемся уравнением электромагнитной индукции
![]() = -[(dF)/dt] Максвелла для шести замкнутных контуров с центром O
(рис.2). Результаты расчетов приведены в таблице.
= -[(dF)/dt] Максвелла для шести замкнутных контуров с центром O
(рис.2). Результаты расчетов приведены в таблице.![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
в то время как в ветвях, продольных направлению движения, они не возникают.
Так как длины ветвей сеток одинаковы, а магнитная индукция в рассматриваемом
участке однородна, то
,
в то время как в ветвях, продольных направлению движения, они не возникают.
Так как длины ветвей сеток одинаковы, а магнитная индукция в рассматриваемом
участке однородна, то
![]() этих ветвей равны
между собой. Их направление выбирается на основании правила правой руки. Здесь принято
этих ветвей равны
между собой. Их направление выбирается на основании правила правой руки. Здесь принято
![]() = 1 в относительных единицах. При составлении схемы
замещения сетки, показанной на рис.2, учтены направления
= 1 в относительных единицах. При составлении схемы
замещения сетки, показанной на рис.2, учтены направления
![]() и
и
![]() .
. 
![]() .
Расчетную схему получим из рис. 2, учитывая, что
.
Расчетную схему получим из рис. 2, учитывая, что
![]() = 0.
Комплексные сопротивления отдельных ветвей сетки одинаковы и принимаются равными
Z0 = r0 + jwL0 = l + jl
относительных единиц.
= 0.
Комплексные сопротивления отдельных ветвей сетки одинаковы и принимаются равными
Z0 = r0 + jwL0 = l + jl
относительных единиц. ![]() контуров от центра к краям рассматриваемого
участка k[a/4] (где k = 1, 2, 3, 4, 5, 6 номера контуров рис. 3а, в).
контуров от центра к краям рассматриваемого
участка k[a/4] (где k = 1, 2, 3, 4, 5, 6 номера контуров рис. 3а, в). ![]() . Расчетную схему также получим из рис.
2, учитывая, что
. Расчетную схему также получим из рис.
2, учитывая, что
![]() = 0. Комплексные сопротивления ветвей
исходной схемы заменяются активными сопротивлениями и приняты равными
Z0 = r0 = 1 относительных единиц.
= 0. Комплексные сопротивления ветвей
исходной схемы заменяются активными сопротивлениями и приняты равными
Z0 = r0 = 1 относительных единиц.