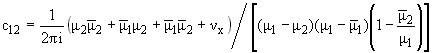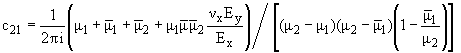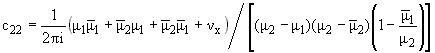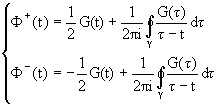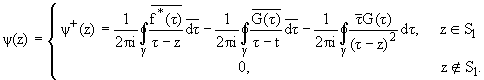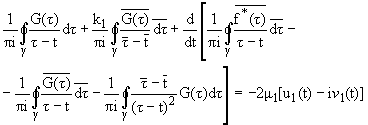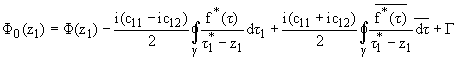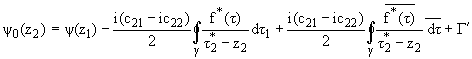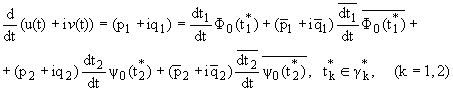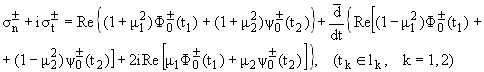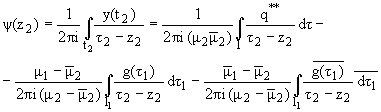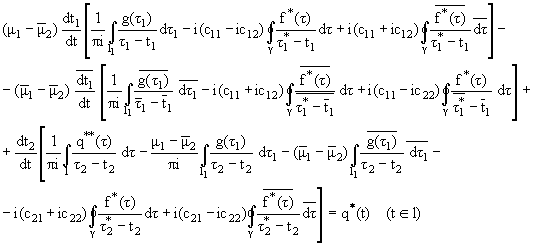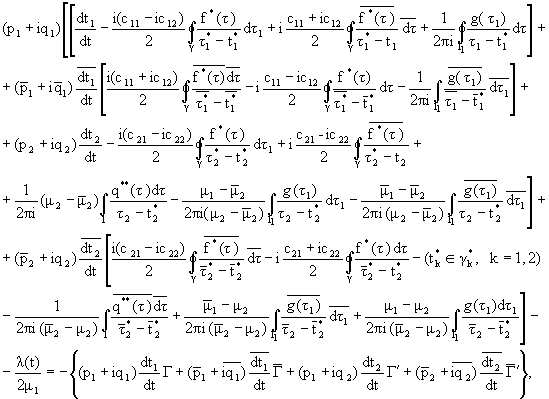УДК 539.3

   The fracture problem of the materials and constructions constitutes of the contemporary topics of the mechanics of deformable bodies. Although the fracture mechanism cannot be only referred to a phenomenon of crack propagation, however the examination of the conditions under which the body starts creating a crack or a system of cracks which later propagate in it, constitutes one of the main and interesting sides of the fracture problem. This side of the problem is referred to the study of the stress-strain state of the body in the region of the imperfections (defects) and the singular points.
   The study of the problem of reinforced plates and shells becomes more complex when in the body imperfections of the form holes, crack, notch, inclusion etc exist. In this case the determination of the interaction of the two opposite factors, such as the reinforcement of the body and its weakening have a great importance.
   1. Let us have an infinite anisotropic (orthotropic) body S with a crack l which is loaded in infinite with the stresses 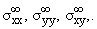On a certain region g of the plate, S where the crack l exists, an elastic isotropic inclusion S₁ it is put which has as aim the reinforcement of the plate because the crack starts propagating.
   The boundary conditions of the above problem are as follows.
   a) On the contact boundary g between the body S and the inclusion S₁ we have equal displacements, as well as equal and opposite stresses i.e.

м п н п о d dt [ u1(t) + iv1(t)] = d dt [ u(t) + iv(t)] sn1 + ist1 = -(sn + ist) = f*(t).

(1)

   b) On the two lips of the crack l the loadings are generally given:

sn± - is1± к кt ˙

(2)

   The complex potentials F₀(z₁) and y₀(z₂), on the basis of which the stress-strain state of the cracked plate, which is loaded in the infinite and on which concentrated force X + iY on the point z₀ acts can be studied, are given in the form [1-4]:

F(z1) = 1 2pi у х l1  j(t1) t1 - z1 dt1 + G + c11X + c12Y z1 - x1 y(z2) = 1 2pi у х l2  j(t2) t2 - z2 dt2 + Gў + c21X - c22Y z2 - x2

(3)

where j(t_k), y(t_k)-densities on the l_k (k = 1,2) and

zk = x + mky,   xk = x0 + mky0;   z = x + iy,   z0 = x0 + iy0

and m_k (k = 1,2) are the roots of the equation:

m4 + ж з и Ex Gxy - 2nx ц ч ш m2 + Ex Ey = 0   (Im mk > 0)

with E_x, E_y, n_x, n_y being elastic constants of the plate in directions x and y respectively, G_xy is the shear modulus. Apart this, for the constants G, G^ў we know that:
   Now, we shall proceed to the determination of the complex potentials of the composite cracked plate (S and S₁).
   For the finite elastic isotropic inclusion S₁ the complex potential is given in the form:

F(z) = м п н п о F+(z) = 1 2pi у х g1  G(t) t - z dt, z О S1 0, z П S1

(4)

   The stresses and the displacements on the boundary g of the inclusion are given by the relationships [1]:

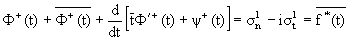(5)

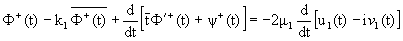(6)

where k₁ = [(3 - v₁)/(1 + v₁)], m₁ = [(E₁)/(2(1 + v₁))] and E₁, v₁ being the elastic constants of the indusion S₁.
   Taking into consideration the Plemelj formulae for the function F(z) when z ® t, t О g [1,5]

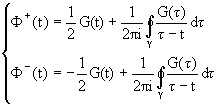(7)

and solving Eq. (5) to obtain y⁺(t), the expression of the other complex potential y(z) takes the following form:

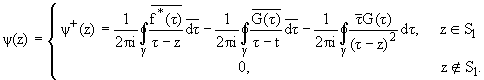
(8)

   Substituting, next, the limit values of F(z), y(z) z ® t О g₁, on the basis of Plemelj formulae, in Eq. (6) we obtain the following singular integral equation

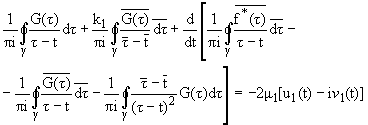(9)

where l(t) = 2m₁[d/dt](u₁(t) + in₁(t)), G(t) = [(f^*(t))/(1 + k₁)] + [(l(t))/(1 + k₁)] - density of Cauchy integral.
   On the anisotropic (orthotropic) cracked plate where along g the effect of the inclusion is transmitted, it is created such a stress-strain field that can be described by the complex potentials F₀(z₁) and y₀(z₁)

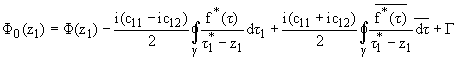
(10)

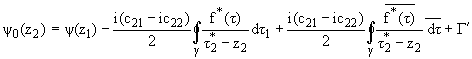
(11)

where F(z₁) = [1/(2pi)]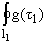/ (t₁ - z₁)]dt₁, y(z₂) = [1/(2pi)]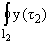/ (t₂ - z₂)]dt₂, g(t₁), y(t₂)-unknown densities along L₁, L₂ and t_k^* = x + m_ky, with x + iy = z (k = 1,2).
   Now, we shall describe the boundary conditions (1) and (2) by the aid of the boundary values of complex potentials (10) and (11) on the basis of Plemelj formulae.
   The stress components s_xx, s_yy, t_xy and the displacements for any point of the anisotropic plate are given by and of complex potentials by the following expressions [3]:

м п н п о sxx = 2Re[ m12F0(z1) + m22y0(z2)] syy = 2Re[ F0(z1) + y0(z2)] txy = -2Re{ m1F0(z1) + m2y0(z2)}

(12)

and

м н о u(z) = 2Re[ p1j0(z1) + p2y0(z2)] n(z) = 2Re[ q1j0(z1) + q2y0(z2)]

(13)

where p_j = [(m_j²)/(E_x)] - [(v_y)/(E_x)], q_j = [1/(E_ym_j)] - [(v_x)/(E_y)]m_j  (j = 1,2).
   By derivating Eq. (13) and taking into account the relationship

sn + isi = 1 2 (sxx + syy) - e-2iq 2 (sxx - syy + 2isxy)

(14)

we obtain the following relationships on the boundaries considered:

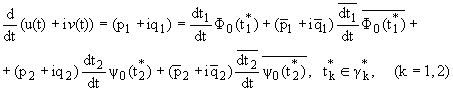(15)

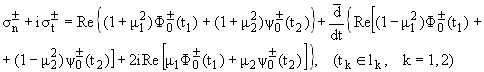(16)

   Solving for y⁺(t₂) - y_-(t₂) after some algebra and taking into account the Plemelj formulae we obtain:

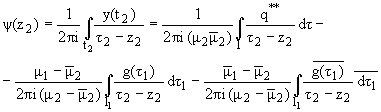(17)

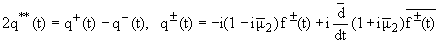where
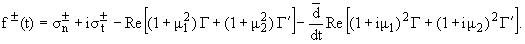   2. By substraction of the Eq. (16) and taking into account the Plemelj formulae for the complex potentials F₀(z₁) and y₀(z₂), when z_k ® t_k О l_k k = 1, 2 after some algebra the following singular integral equation results:

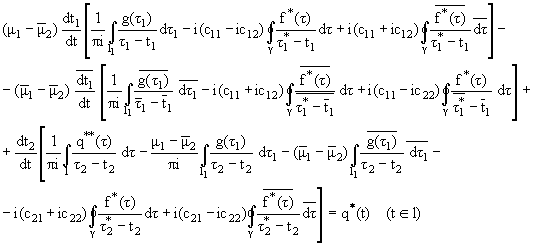(18)

which describes the conditions (2) and where q^*(t) = q⁺(t) + q^-(t).
   Finally, substituting in Eq. (15) the limit values of the complex potentials by the Plemelj formulae we have the following singular integral equation on the g of the anisotropic plate.

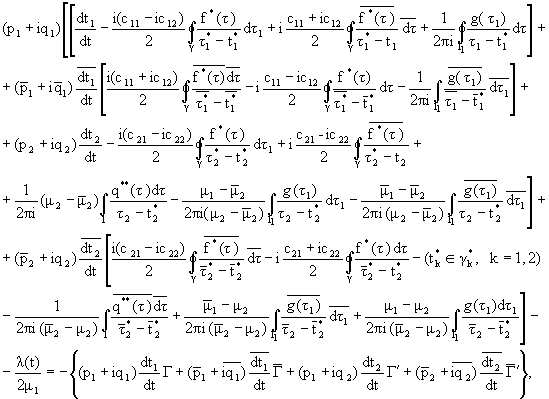(19)

   Eqs. (9), (18) and (19) are completed with the single valuedness condition for the displacements on the crack l

у х l  d dt [(u+ - u-) + i(n+ - n-)]dt = 0

(20)

and the equilibrium condition of the stresses on g

у х g  f*(t)ds = 0

(21)

where Eq. (20), after substitution of the relationships for the displacements through the complex functions on the basis of Eq. (15) and using Plemelj formulae, will take the following form

(22)

   Eqs. (9), (18), (19), (21) and (22) give the possibility to describe the stress-strain state field of the plane cracked orthotropic plate which is reinforced with an elastic isotropic inclusion.
   The work is fulfilled in the framework of agreement on scientific collaboration between Athen National Technical University and the Institute of Mechanics of NAS RA

     National Technical University of Athens