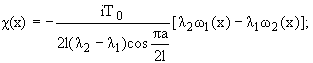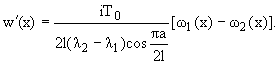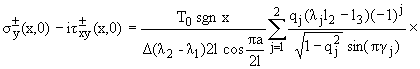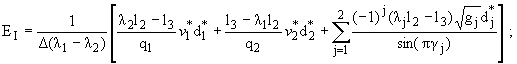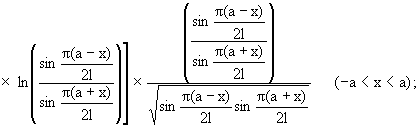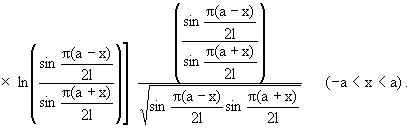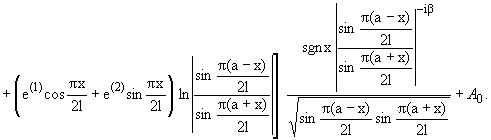УДК 539.375

   Рассматривается напряженное состояние составной упругой плоскости, ослабленной периодической системой трещин, на одном из берегов которых заданы компоненты напряжения, а на другом - компоненты смещения. Выведены определяющие уравнения, описывающие поставленную задачу, в виде системы двух сингулярных интегральных уравнений второго рода с ядром Гильберта и построено ее замкнутое решение.
   Пусть упругая составная плоскость, состоящая из двух полуплоскостей с различными модулями сдвига m₁, m₂ и коэффициентами Пуассона n₁, n₂, на линии стыка полуплоскостей ослаблена периодической, с периодом 2l, системой трещин длиной 2a, на верхнем берегу которых заданы напряжения s₁(x) - it₁(x), а на нижнем - компоненты смещения u₂(x) + in₂(x) и главный вектор действующих там напряжений s₂ - it₂.
   Для определенности, как и выше, все величины, описывающие напряженно-деформированное состояние верхней и нижней полуплоскостей, снабдим верхними индексами 1 и 2 соответственно. Из-за периодичности поставленной задачи будем рассматривать напряженное состояние составной бесконечной полосы шириной 2l, которая на линии стыка двух полубесконечных полос, занимающих области D_± = {-l Ј x Ј l; 0 Ј ±y < Ґ}, ослаблена центральной трещиной длиной 2a, на верхнем берегу которой заданы компоненты напряжения, а на нижнем - компоненты смещения. При этом на граничных линиях полос x = ±l будут иметь место условия симметрии. Тогда поставленную задачу для компонентов смещения u^(j)(x,y), v^(j)(x,y) (j = 1,2), удовлетворяющих уравнениям Ляме в соответствующих областях D_±, и компонентов напряжений (x,y), 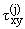(x,y) (j = 1,2), связанных со смещениями законом Гука, математически можно сформулировать в виде следующей граничной задачи:

а) б) u(1)(x,0) + iv(1)(x,0) = u(2)(x,0) + iv(2)(x,0) (l > |x| > a); в) г) u(2)(x,0) + iv(2)(x,0) = u2(x) + iv2(x) (|x| < a); д) (0 < y < Ґ); е) (-Ґ < y < 0).

(1)

   Чтобы построить решение этой смешанной граничной задачи, введем в рассмотрение функции c(x) и w(x), описывающие скачок напряжений, действующих на берегах трещины, и приведенное раскрытие трещины, определяемые формулами

[ u(1)(x,0) + iv(1)(x,0)] - [ u(2)(x,0) + iv(2)(x,0)] = w(x)/q22.

(2)

   Сначала решим вспомогательную задачу, аналогичную (1), с той лишь разницей, что условия (1в) и (1г) заменены условиями (2), и определим компоненты напряжения верхнего берега трещины и компоненты смещения нижнего берега трещины при помощи функций c(x) и w(x). С этой целью используем бигармонические функции напряжения для областей D_± и представим их в виде рядов:

Fj(x,y) = Ґ е k=1  [ Ak(j) - (-1)jakyBk(j)] exp [ (-1)j+1aky] cosakx,

(3)

где a_k = pk/l, а A_k^(j),  B_k^(j) (j = 1,2;  k = 1, 2, ј) - неизвестные коэффициенты, подлежащие определению.
   Легко проверить, что при таком выборе функций F_j(x,y) (j = 1,2) последние четыре условия (1) удовлетворяются тождественно. Удовлетворяя остальным условиям вспомогательной задачи и определив коэффициенты A_k^(j),  B_k^(j) (j = 1,2) через функции c(x) и w(x), удовлетворим условиям (1в) и (1г). Тогда после некоторых преобразований для определения функций c(x) и w(x) получим следующую систему сингулярных интегральных уравнений второго рода с ядром Гильберта:

wў(x) + a1i 2l a у х -a  ctg p(s - x) 2l wў(s)ds + a2i 2l a у х -a  ctg p(s - x) 2l c(s)ds = F1(x); c(x) - b1i 2l a у х -a  ctg p(s - x) 2l wў(s)ds + b2i 2l a у х -a  ctg p(s - x) 2l c(s)ds = F2(x),

(4)

которую нужно рассматривать при условиях

a у х -a  c(x)dx = T0;    w(±a) = 0.

(5)

   Отметим, что здесь и в дальнейшем будут сохранены обозначения работы [1].
   Приступим к решению ситемы (4). Система (4) почти точностью совпадает с системой (4) из [1], с той лишь разницей, что вместо ядра Коши здесь фигурирует ядро Гильберта. Следовательно, как и в [1], решение этой системы можно свести к решению отдельных интегральных уравнений с ядром Гильберта в случае, когда уравнение (2.2) из [1] имеет два различных корня, и последовательному решению двух интегральных уравнений в случае двух одинаковых корней.
   В случае, когда уравнение (2.2) из [1] имеет два различных корня l₁ и l₂, отличных от нуля, умножая первое из уравнений (4) поочередно на l₁ и l₂ и складывая со вторым, получим следующие два независимых интегральных уравнения:

jj(x) + iqj 2l a у х -a  ctg p(s - x) 2l jj(s)ds = Qj(x)    (j = 1,2;  |x| < a).

(6)

   При этом функции j_j(x) = c(x) + l_jw^ў(x) должны удовлетворять также условиям

a у х -a  jj(x)dx = T0    (j = 1,2).

(7)

   Чтобы построить решение уравнений (6), перейдем к новым переменным по формулам

t = tg ps 2l ; t = tg px 2l

и введем обозначения

a = tg pa 2l ; Aj = iqj p a у х -a  tjj*(t) 1 + t2 dt; jj*(t) = jj ж з и 2l p arctgt ц ч ш ; Qj*(t) = Qj ж з и 2l p arctgt ц ч ш .

   Тогда уравнения (6) и условия (7) примут вид:

jj*(t) + iqj p a у х -a  jj*(t)dt t - t = Qj*(t) + Aj;    a у х -a  jj*(t) 1 + t2 dt = pT0 2l     (j = 1,2; |t| < a).

   Решая полученные уравнения [2,3] и возвращаясь к исходным неизвестным, для функций c(x) и w^ў(x) в случае, когда верхние берега трещин свободны от напряжений, а на нижних берегах действуют абсолютно жесткие штампы с плоскими основаниями (u₂(x) = 0, v₂(x) = const), получим формулы

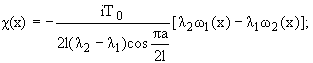
(8)

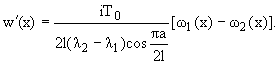
(9)

При этом разрушающие напряжения 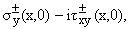действующие вне трещины, даются формулами

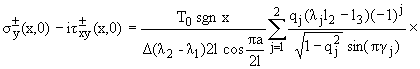× G0(j) cos px 2l + iG1(j) sin px 2l к к к sin p(x + a) 2l к к к gj   к к к sin p(x - a) 2l к к к 1-gj   + E1 (a < |x| < 1).

(10)

Здесь

Gm(j) = 1 2 [ (i + a)-gj (i - a)gj-1 + (-1)m (i + a)gj-1 (i - a)-gj ], (m = 0,1;  j = 1,2);

nj* = (1 + qj)iG1(j) G0(j) + ia(1 - 2gj)G1(j) ;       dj* = qjT0 2l(1 + qj) [G1(j)a1(j) - iG0(j)a0(j)]     (j = 1,2).

   Отметим, что при получении этих формул было иcпользовано значение интеграла

a у х -a  tm(a + t)gj (a - tgj-1) 1 + t2 dt = -(i)m+1 p(1 + qj) qjeip (gj-1) Gm(j)    (m = 0,1;  j = 1,2).

   Из полученных выражений легко определить коэффициенты интенсивности  в  точках  x = ±a.  Если  материалы  полуплоскостей  таковы,  что Re g₁ > Re g₂, то будем иметь

× й к л G0(j)cos pa 2l + i(-1)j sin pa 2l щ ъ ы     (j = 1,2).

(11)

   Теперь рассмотрим случай, когда материалы полуплоскостей таковы, что уравнение    (2.2)    из    [3]    имеет    два    одинаковых    корня    l₁ = l₂ = l = (a₁ - b₂)/2a₂. Тогда по процедуре, приведенной в работе [1], решая поочередно два интегральных уравнения, получим замкнутое решение поставленной задачи. Не останавливаясь на этом, опять-таки приведем решение задачи в случае, когда верхние берега трещин свободны от напряжений, а на нижних берегах действуют абсолютно жесткие штампы с плоскими основаниями. Оно имеет вид:

(12)

c(x) = -   __ Цg1   cos pa 2l й к л b(1)cos px 2l + b(2)sin px 2l - l1 ж з и a(1)cos px 2l + a(2)sin px 2l ц ч ш ×

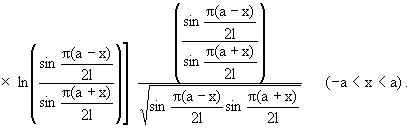(13)

   Разрушающие контактные напряжения 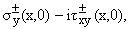действующие вне трещины, в этом случае имеют вид

(14)

где a^(j), b^(j), c^(j), e_j, e^(j), A₀, g₁ (j = 1,2) - известные постоянные, значения которых здесь не приводятся.
   Из (14) можно заключить, что в рассматриваемом случае контактные напряжения в концевых точках трещины помимо степенной особенности имеют также логарифмическую особенность.

     Институт механики НАН РА

Литература

     1. Акопян В.Н.  - Изв. НАН Aрмении. Механика. 1995. Т.48. С.57-65.
     2. Мусхелишвили Н.И.  Некоторые основные задачи математической теории упругости. М. Наука. 1966. 708 с.
     3. Гахов Ф.Д.  Краевые задачи. М. Наука. 1977. 640 с.

---