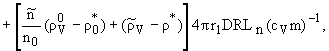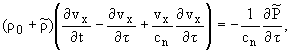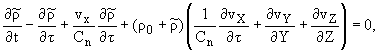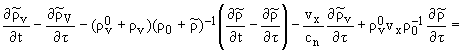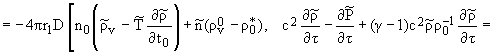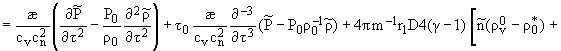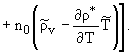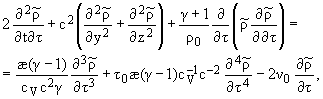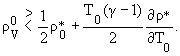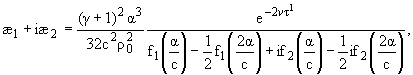УДК 539.1

   Рассматривается задача определения параметров движения трехфазной среды, состоящей из газа, пара и очагов его конденсации - сферических капель, при прохождении через нее мощного акустического пучка. Предположено, что возмущения фонового постоянного состояния малы и скорости всех фаз v одинаковы. Капли распределены равномерно с начальной концентрацией n_o и радиусом r₁. Считается, что эффективная плотность среды приближенно равна плотности газа r. Уравнение движения имеет вид

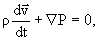
(1)

где P суммарное давление газа и пара [1].
Для плотности газа r имеет место уравнение неразрывности

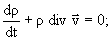
(2)

   для концентрации капель -

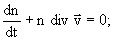
(3)

   для пара, конденсирующегося на каплях-

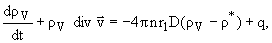
(4)

где D - коэффициент диффузии пара в газе [1], q - источник массы, r^*(T) - плотность насыщения паров.
   Уравнение энергии получается из второго начала термодинамики

T dS dt = cV dT dt + P d dt ж з и 1 r ц ч ш .

(5)

Уравнение (5), уравнение
и уравнение притока тепла [1] дают

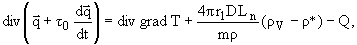
(6)

где T - температура, L - энергия, выделяющаяся при конденсации одной молекулы воды, m - масса одной капли, Q - источник тепла [1], t_o - коэффициент тепловой релаксации.
   В стационарных условиях (без волны) все искомые величины снабжаются индексом 0, причем условия равновесия

q = 4pr1 Dn0 (rV0 - r0*),    Q = 4pr1 L(mr0)-1(rV0 - r0*).

(7)

   Обозначим возмущения параметров тильдой. При этом из уравнения энергии (5), (6) получим

dP dt - a2 dr dt = æ cV (DP - P0 r-1D r) - t0 æ cV ¶ ¶t (DP - P0 r0-1D r) +

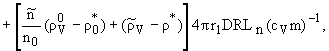(8)

где взято уравнение идеального газа

P = R rT,   a2 = gPr-1,

(9)

g - показатель адиабаты, D - лапласиан.
Выберем ось x по нормали к невозмущенной плоской волне, оси y,z - в касательной к ней плоскости. Обозначим эйконал

t = x cn - t, ¶ ¶t к к кx = ¶ ¶t , к к кt - ¶ ¶t , ¶ ¶x к к кt = 1 cn ¶ ¶t ,

(10)

где c_n - скорость невозмущенной волны.
   Тогда, учитывая порядки малости возмущений

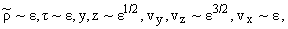(11)

а также то, что для скорости звука

a2 » c2 + 2(g - 1) c2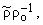

где c - невозмущенная скорость звука, из (1)-(4) и (8) получим следующую систему уравнений:

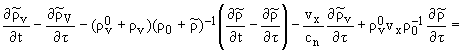(12)

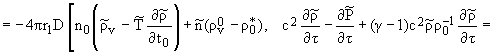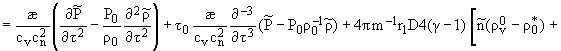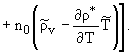   Из уравнений (12) в порядке 0 (1), т.е. оставляя лишь линейные члены с [(¶)/(¶t)], получим условия совместности

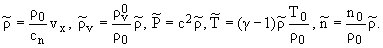(13)

Учитывая (13) в основных порядках w, w^1/2, после исключения всех производных по t, линейно входящих в (12), получим эволюционное уравнение для 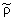следующего вида:

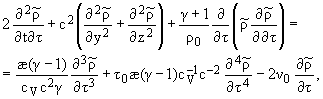(14)

где

n0 = 2pr1Dg1Ln0(1 - g)c-2m-1,  n1 = r0-1(2rv0 - r0) - T0r0-1(g - 1) ¶r* ¶T0 .

   Второе слагаемое в (14) дает дифракцию, третье - нелинейность, четвертое - тепловую диссипацию, пятое - дисперсию и шестое - линейное усиление или затухание волны, связанные с наличием пара и капель.    Оставляя только первое и последнее слагаемое, т.е. пренебрегая дифракцией, нелинейностью и теплопроводностью, можно получить значение 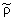, откуда вытекает, что поскольку L > 0, условия усиления или затухания волны имеют вид

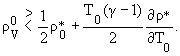(15)

Условие (15) другим методом получено в [1]. Исходя из верхнего знака в неравенстве (15) в [1,2] обсуждается механизм конденсации пара за счет звуковой волны. Исследование решений эволюционного уравнения (14) позволяет более детально изучить свойства решений за счет нелинейности, дифракции, дисперсии и диссипации. Отметим, что можно получить солитонные решения уравнения (14) [3] и изучить их устойчивость [4], причем в случае нижнего знака в (15) солитоны устойчивы, а верхнего - неустойчивы.
   При наличии подаваемых на облако квазимонохроматических волн решение (14) ищем в виде

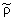=  1 2 м н о A(t, tў, y, z) exp(iat - ntў - iwtў) +    + B(t, tў, y, z) exp[2(iat - ntў - iwtў)] + k.c. ь э ю ,

(16)

где a - основная частота невозмущенной волны, tў = xc_n^-1. Тогда, повторяя выкладки [3], [5], из (14) найдем нелинейное уравнение Шредингера

ia ж з и ¶A ¶t + ¶A ¶tў ц ч ш + c2 2 D1A = (ae1 + æ2)|A|2A,

(17)

где

æ1 = -3wx, æ2 = - ж и n - 3 2 n0 ц ш x, w = a3t0(g - 1)(cVc2g)-1, x = a3(g + 1)2 м н о 32r02[9w2 + ж и n + 3 2 n0 ц ш 2   ] ь э ю -1   exp(-2ntў), n = 1 2 a2æ(g - 1)(cVc2g)-1 + n0,

(18)

w - модулированная частота, n - линейная диссипация.
   Отыскивая решение (17) в виде узких пучков [3], [5]

A = bf -1(tў) exp ж з и -r2 2r02f 2 + ij ц ч ш ,   j = s(tў) + r2 2R(tў) ,

(19)

где r² = y² + z², r₀ - начальный радиус осесимметричного пучка, b - постоянная амплитуда на входе в среду (x = 0),  f(tў) - безразмерная ширина пучка, s - набег фазы, ac_n^-1R(tў) - радиус кривизны фронта пучка, из (17), с учетом (19), получим уравнение

d2f dtў 2 = M f3 + 2æ2nb2 af ,

(20)

где

M = a-2 ж з и c4 r04 + 2æ1 b2c2 r02 - æ22b4 ц ч ш ,

(21)

причем начальные условия для f имеют вид

f(0) = 1, df(0) dtў = F, F = 2c2 aR0 - æ2b2 a ,

(22)

где R₀ есть R(0) в начальном сечении пучка.
   Можно численно решить (20), (22) и получить законы фокусирования пучка, а из (19) - амплитуду волны в облаке.
   В случае, если |ntў| << 1, т.е. на небольших относительных участках с учетом малости диссипации, можно в (20) отбросить второе слагаемое правой части и проинтегрировать указанное уравнение. Оно будет иметь вид [3], [5]

f2(tў) = M F2 + M + ж и F2 + M ц ш й л tў + F(F2 + M)-1 щ ы 2   .

(23)

   Интересно отметить, что M > 0 (M < 0) соответствует дефокусировке (фокусировке) пучка, причем слагаемое æ₂b⁴ в (21) за счет нелинейной диссипации приводит к самофокусировке.
   Можно также учесть, следуя [2], влияние переменного радиуса капель на пороговые значения частот или зависимость от него плотности водяного пара, что не отражается на развиваемой здесь методике.
   Уравнения (17), (18) недостаточно точно учитывают роль дисперсии и коэффициента n, которые для небольших a должны быть учтены путем сравнения с линейным дисперсионным соотношением [6], для рассматриваемой задачи имеющим вид [1]

W2 - c2k2 = ick2n1 W + is1 , c = 4pL r1(g - 1)n0Dm-1, s1 = 4pr1Dn0,

(24)

где решение пропоционально exp(ikx - iWt). Сравнивая последнее с (16), получим

W = a + w,    k = a c + i n c .

С учетом того, что w,n << a, из (24) получим

f1 ж з и a c ц ч ш = w = 1 2 cas1n1c-2 (a2 + s12)-1, n = n2 + a2æcV-1c-2g-1(g - 1) = - f2 ж з и a c ц ч ш . n2 = - 1 2 ca2n1c-2(a2 + s12)-1,

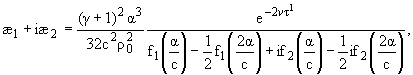(25)

причем в n учтена диссипация, обусловленная теплопроводностью (18), а в æ_1,2 следует заменить n₀ на n₂.
   Таким образом, равенства (16)-(23) имеют место и для уточненной согласно [1] среды с учетом того, что a является небольшой величиной, и результаты, получаемые из эволюционного уравнения (14), выведенного для больших a, должны быть уточнены.
   Значения w, n берутся не из (18), а из (25). При этом дисперсия дается не заведомо малой величиной (18) (в силу малости t₀), а значительно большей величиной (25), диссипация зависит от частоты, как и в [1]. Указанный метод сшивания результатов, полученных из эволюционного уравнения (14), с линейным дисперсионным соотношением (24) является общим и удобным.

     Институт механики НАН РА

Литература

     1. Немцов Б.Е. - ДАН СССР. 1990. Т. 314 N 2. С. 355-358.
     2. Нетреба С.Н. - Изв. РАН. Физика атмосферы и океана. 1997. Т.33. N 3. 412-413.
     3. Багдоев А.Г., Шекоян А.В. - Акустический журнал. 1999. Т. 45. N 2. С. 149-156.
     4. Багдоев А.Г., Шекоян А.В.  - Из в. НАН Армении. Физика. 2000. Т. 35. N 2. С. 85-89.
     5. Bagdoev A.G., Shekoyan A.V. - Conversion Potential of Armenia and ISTC International Seminar. Proceedings. Part I. Yerevan. 2000. P. 102-105.
     6. Багдоев А.Г., Шекоян А.В., Даноян З.Н. - Из в. НАН Армении. Физика. 1997. Т. 32. N 6. С. 13-22.

---