МАТЕМАТИКА
УДК 517.5
А.Г. Багдасарян
Об обобщенных пространствах типа Никольского - Бесова
с неограниченной точностью
(Представлено чл.-кор. НАН РА Г.Г. Геворкяном 6/XII 2001)
Хорошо известно, что, изучая пространства
следов функций из H-пространств Соболева - Лиувилля, мы приходим к
B-пространствам Никольского - Бесова (см. [1,2]). Эта же особенность возникает
при исследовании интерполяционных свойств пар H-пространств методом
"вещественной" интерполяции (см. [3,4]).
Исследуя отмеченные свойства H-пространств,
порожденных полными многогранниками, мы ввели (см. [5]) соответствующие
пространства
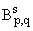 (m) типа
Никольского - Бесова, с функцией m(x), отвечающей заданному многограннику.
(m) типа
Никольского - Бесова, с функцией m(x), отвечающей заданному многограннику.
Во всех указанных случаях функция m(x) стремится к бесконечности при
|x| ® Ґ, что
позволяет при определении B-пространств применять метод покрытия Rn
(см. [3-5]).
В настоящей заметке мы определяем
B-пространства посредством "вещественной" интерполяции соответствующих пар
H-пространств. Этот подход дает возможность определения пространств
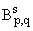 (m) типа Нокольского -
Бесова и для функций m(x), не
стремящихся к бесконечности при |x| ® Ґ.
(m) типа Нокольского -
Бесова и для функций m(x), не
стремящихся к бесконечности при |x| ® Ґ.
Будем пользоваться следующими обозначениями:
Rn - n-мерное евклидово пространство, S - класс Шварца, F - оператор
преобразования Фурье, C - пространство непрерывных функций,
(A0, A1)q,q,
[A0, A1]q -
интерполяционные пространства, полученные методами "вещественной" и
"комплексной" интерполяции для заданной пары { A0, A1}
(см. [3,4]).
Обозначим через G+ множество
положительных функций m О
CҐ(Rn) таких, что для любого
мультииндекса a с компонентами из множества { 0;1}
| |xa
Da m(x)| Ј cm(x), c >
0, x О
Rn, |
n
Х
i=1
|
xi № 0. | |
(1) |
Определение 1. Пусть 1 < p
< Ґ, -Ґ < s < Ґ, m О G+. Положим
| Hps(m; Rn) є
Hps(m) = { f О Sў; || f ||H = || F-1{msF f} || Lp(Rn) <
Ґ}. | |
Для
функций m(x), непрерывных в
Rn, бесконечно дифференцируемых вне координатных осей и
удовлетворяющих оценке (1), H-пространства понимаются как пополнение
S
в
определенной выше норме.
Рассмотрим оператор типа "лифтинга":
Определение 2. Пусть 1 < p
< Ґ, 1 Ј q Ј Ґ, -Ґ < s < Ґ, m О G+. Положим
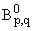 (m) = ( Hp1(m), Hp-1(m))[1/2],q, (m) = ( Hp1(m), Hp-1(m))[1/2],q, | |
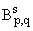 (m) = Ims (m) = Ims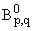 (m) = { f О Sў; Ims f О (m) = { f О Sў; Ims f О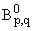 (m)}. (m)}. | |
Следующая теорема дает описание
интерполяционного пространства, фигурирующего в определении 1.
Теорема 1. Пусть 1 < p <
Ґ, 1 Ј q Ј Ґ, 0 < q < 1, m О G+. Тогда
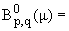 |
м
н
о |
f О Sў; || f ||B = |
ж
з
и |
|
Ґ
у
х
0
|
|| F-1 |
м
н
о |
|
t1-qmq
m + t
|
F f |
ь
э
ю |
|| |
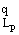 |
dt
t
|
ц
ч
ш |
[1/q]
|
< Ґ |
ь
э
ю |
| |
(с
обычными видоизменениями при q = Ґ).
Для введенных H и B-пространств доказываются
интерполяционные формулы "вещественной" и "комплексной" интерполяции.
Теорема 2.
а) Пусть m О G+, -Ґ < s0 № s1
< Ґ, 1 < p < Ґ, 1
Ј q Ј Ґ, 0 < q < 1,
s = s0(1-q) + s1q.
Тогда
|
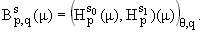
|
б) Пусть m О
G+, -Ґ <
s0 № s1 < Ґ, 1 < p < Ґ, 1 Ј q, q0, q1 Ј
Ґ, s = (1-q)s0 + qs1, 0
< q < 1. Тогда
|
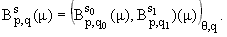
|
в) Пусть m О
G+, -Ґ < s <
Ґ, 1 < p < Ґ, 1 Ј q0, q1 Ј
Ґ, 0 < q < 1,
[1/(q*)] = [((1-q))/(q0)] + [(q)/(q1)]. Тогда
|
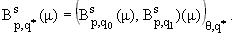
|
г) Пусть m О
G+, -Ґ <
s0, s1 < Ґ, 1 Ј q0, q1 Ј
Ґ, 1 < p0, p1 < 0, 0 <
q < 1, s = (1-q)s0 + qs1,
[1/(p*)] = [((1-q))/(p0)] + [(q)/(p1)], [1/(q*)] = [((1-q))/(q0)] + [(q)/(q1)]. Тогда
|
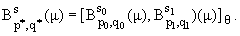
|
д) Пусть m О
G+, -Ґ <
s0 № s1 < Ґ, 1 < p < Ґ, 1 Ј q0, q Ј Ґ, 0 < q < 1, s = (1-q)s0 + qs1. Тогда
|
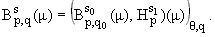
|
Следующие теоремы дают описание B-пространств
с точки зрения теорем вложения разных метрик.
Теорема 3. Пусть m, n О
G+, 1 < p < Ґ. Тогда
Теорема 4. Пусть m, n О
G+, 1 < p < Ґ, 1 Ј q Ј Ґ.
Для того чтобы имело место вложение
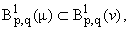 необходимо и достаточно, чтобы
необходимо и достаточно, чтобы
| n(x) Ј cm(x), c >
0, x О
Rn. | |
Теорема 5. Пусть 1 < p <
Ґ, 1 Ј q Ј Ґ, m
О G+, [1/p] + [1/(pў)] = [1/q] + [1/(qў)] = 1. Для того чтобы
имело место вложение
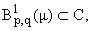 необходимо и достаточно, чтобы
необходимо и достаточно, чтобы
В заключение приведем теорему о следах для
H-пространств, порожденных вполне правильным многогранником.
Определение 3. Непустой
многогранник N, с вершинами из первого координатного угла
называется полным, если начало координат является вершиной N и
N имеет вершины на каждой оси координат,
отличные от начала координат.
Полный многогранник N называется
вполне правильным, если внешние нормали (n - 1)-мерных
некоординатных граней N имеют только положительные координаты.
Пусть задан вполне
правильный многогранник N с
вершинами a0, a1, ј , aM. Сопоставим многограннику N функцию
| m(x) = |
ж
и |
M
е
j=0
|
x2aj |
ц
ш |
[1/2]
|
. | |
Пусть далее вершины многогранника N имеют следующие n-тые координаты: 0, m1, ј , mN, причем 0 < m1 < ј < mN. Тогда функцию m(x) можно представить в
эквивалентной форме
| m(x) ~ |
ж
и |
m02(xў) + |
N
е
j=1
|
xn2mj mj2(xў) |
ц
ш |
[1/2]
|
, xў = (x1, ј , xn-1), | |
где
функция m0(xў) отвечает проекции многогранника N на
Rn-1, а функции mj(xў) - проекциям на Rn-1
сечений многогранника N гиперплоскостями {x О Rn; xn = mj}, j = 1, ј , N.
Рассмотрим следующий оператор следа:
| (Tr f)(xў) = f(xў,0), f О
S(Rn). | |
Теорема 6. Пусть N -
вполне правильный многогранник с функцией m(x). Пусть далее 1 < p <
Ґ, m1 > [1/p], l
= m01-[1/(pm1)] · m1[1/(pm1)]. Тогда оператор
следа есть ретракция Hp1(m; Rn) на Il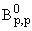 ([(m0)/(m1)]; Rn-1).
([(m0)/(m1)]; Rn-1).
Это означает (см. [3,4]), что оператор следа
- линейный ограниченный оператор, для которого существует линейный ограниченный
оператор продолжения s такой, что Trs = E.
Ереванский государственный
университет
Литература
1. Никольский С.М. Приближение функций многих переменных и теоремы вложения. М. Наука.
1977. 455 с.
2. Бесов О.В., Ильин
В.П., Никольский С.М. Интегральные представления функций и
теоремы вложения. М. Наука. 1975.
3. Трибель Х. Теория интерполяции. Функциональные
пространства. Дифференциальные операторы. М. Мир. 1980. 664
с.
4. Берг Й., Лефстрем Й.
Интерполяционные пространства. Введение. М. Мир. 1980. 264
с.
5. Багдасарян А.Г. - Изв. АН АрмССР. Математика. 1988. Т.23. N 4. С. 353-365.