МАТЕМАТИКА
УДК 517. 57
К. Л. Аветисян
О дробном интегродифференцировании в классах
гармонических
функций на полупространстве со смешанной
нормой
(Представлено академиком Н.У. Аракеляном 30/VIII 2001)
1. Пусть Rn - n-мерное евклидово пространство, и пусть
x = (x1,..., xn) О Rn, |x|2 = x12 + ј + xn2, dx = dx1 ј dxn. Обозначим через
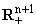 верхнее полупространство пространства Rn+1, т.е.
верхнее полупространство пространства Rn+1, т.е.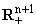 =
Rn × (0, Ґ). Точки этого
полупространства будем представлять как (x,y) = (x1,..., xn,
y), x О Rn, y > 0.
Иногда удобно будет обозначать x0 = y.
=
Rn × (0, Ґ). Точки этого
полупространства будем представлять как (x,y) = (x1,..., xn,
y), x О Rn, y > 0.
Иногда удобно будет обозначать x0 = y.
Для измеримой в
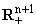 функции f(x,y) положим
функции f(x,y) положим
| Mp(f; y) = ||f||Lp(Rn, dx),
y > 0, 0
< p Ј Ґ. | |
Пространство
Харди hp(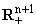 ) в верхнем
полупространстве
) в верхнем
полупространстве
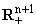 состоит из
всех (комплекснозначных) гармонических функций u(x,y) в
состоит из
всех (комплекснозначных) гармонических функций u(x,y) в
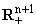 , для которых
, для которых
| ||u||hp = |
sup
y > 0
|
Mp(u;y) < +Ґ. | |
Введем
в рассмотрение следующее квазинормированное
пространство L(p,q,a) (0 < p, q Ј Ґ, a >
0) со смешанной нормой, состоящее из тех измеримых в
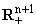 функций f(x,y), для которых конечна
квазинорма (норма при 1 Ј p,q Ј Ґ)
функций f(x,y), для которых конечна
квазинорма (норма при 1 Ј p,q Ј Ґ)
| ||f||p,q,a = |
м
п
п
н
п
п
о |
|
ж
и
|
у
х
|
+Ґ
0
|
yaq-1Mpq(f;
y)
dy |
ц
ш
|
1/q
|
, | |
|
|
|
| |
| |
Через h(p,q,a) обозначим гармоническое подпространство в L(p,q,a). Вопрос о дробном интегродифференцировании в пространствах
со смешанной нормой был поднят Харди и Литтлвудом [1], [2] и может быть
сформулирован следующим образом: как ограниченно действует оператор дробного
интегродифференцирования в пространствах h(p,q,a)? Этот
вопрос детально изучался Флеттом [3], [4], особенно для голоморфных функций в
единичном круге (см. также работу автора [5], в которой были дополнены
результаты Флетта). В полупространстве
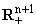 тема дробного
интегродифференцирования изучалась в гораздо меньшей степени. Отметим работы М.
Тейблсона [6], Т. Флетта [7], Буй Хюи Ки [8], А. Э. Джрбашяна [9].
тема дробного
интегродифференцирования изучалась в гораздо меньшей степени. Отметим работы М.
Тейблсона [6], Т. Флетта [7], Буй Хюи Ки [8], А. Э. Джрбашяна [9].
2. Для функции f(x,y),
измеримой и комплекснозначной в
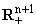 , введем в рассмотрение оператор
дробного интегродифференцирования Римана-Лиувилля (называемый также потенциалом
Рисса):
, введем в рассмотрение оператор
дробного интегродифференцирования Римана-Лиувилля (называемый также потенциалом
Рисса):
| D-af(x,y) = |
1
G(a)
|
|
у
х |
+Ґ
0
|
sa-1f(x,y + s)ds, | |
| D0
f = f, Daf(x,y) = (-1)mD-(m-a) |
¶m
¶ym
|
f(x,y), | |
где a > 0, а m- целое, m - 1 < a Ј m. Если T - ограниченный
оператор, отображающий пространство X в Y, т.e. ||Tf||Y Ј C||f||X, "f О X, то будем писать T : X ® Y.
Нижеследующая теорема описывает действие оператора дробного дифференцирования в
классах Харди hp. Ее доказательство следует из одного неравенства
типа Литтлвуда-Пэли (см. [10]).
Теорема 1. Пусть a > 0, 2 Ј q Ј Ґ и 1 < p Ј q Ј Ґ.
Тогда
|
|
|
| Da : hp ® h(p0,q,a + n/p - n/p0),
| |
| |
| |
Действие дробного оператора D-a в пространствах h(p,q,a)
описано в следующей таблице.
Теорема 2. Пусть 0 <
p,q Ј Ґ, a > 0 - произвольные числа. Тогда
|
| D-b : h(p,q,a) ® h(p,q,a - b), | |
|
|
|
| b = a, 0 < p < Ґ, 0 < q Ј |
min
|
{2,p}, | |
|
|
| a <
b < a + n/p, 0 < p < Ґ, q Ј
p0, | |
| D-b : h(p,q,a) ® h(p0,q0),
| |
| a <
b < a + n/p, 1 Ј p < Ґ, | |
|
|
| 0 < q Ј q0 Ј Ґ, 1
< q0 Ј Ґ, | |
|
|
| b = a + n/p, p = Ґ, 0 < q Ј Ґ, | |
|
|
| b = a + n/p, 0 < p < Ґ, 0 < q Ј Ґ, | |
|
|
| b = a + n/p, 0 < p Ј Ґ, 0
< q Ј
1, | | |
| |
где
p0 = [n/(a + n/p - b)]; h(p,q)
обозначает гармоническое пространство Лоренца
(см. [11], [8]); B - гармоническое
пространство Блоха; BMOh - пространство гармонических в
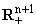 функций с граничными значениями из
BMO(Rn).
функций с граничными значениями из
BMO(Rn).
Для функции u(x,y), гармонической в
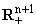 и удовлетворяющей условию
и удовлетворяющей условию
| u(x,y) = O |
ж
з
и |
1
yd
|
ц
ч
ш |
, y ® +Ґ, d
> 0, | |
преобразования Рисса
определяются как
| uj(x,y) = (Rju)(x,y) = - |
у
х |
+Ґ
y
|
|
¶u(x,h)
¶xj
|
dh, 1 Ј j Ј
n. | |
Вектор-функция
F = (u0, u1, ..., un), u = u0,
является системой Рисса сопряженных гармонических функций (см., например, [11]),
т.е. функции uj удовлетворяют обобщенным уравнениям Коши-Римана [11]
|
n
е
j=0
|
|
¶uj
¶xj
|
= 0, |
¶uj
¶xk
|
= |
¶uk
¶xj
|
, 0 Ј j,k Ј
n. | |
(1) |
Эти уравнения равносильны
существованию гармонической в
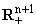 функции f такой, что F = Сf. Заметим, что в случае n = 1
уравнения (1) переходят в обычные уравнения Коши-Римана. При этом функция
F = u0 + iu1 голоморфна относительно переменной
z = x1 + ix0.
функции f такой, что F = Сf. Заметим, что в случае n = 1
уравнения (1) переходят в обычные уравнения Коши-Римана. При этом функция
F = u0 + iu1 голоморфна относительно переменной
z = x1 + ix0.
В следующей теореме устанавливается
ограниченность оператора гармонического сопряжения (т.е. преобразований Рисса
Rj) в пространствах h(p,q,a) при всех
допустимых 0 < p,q Ј Ґ, и,
тем самым, обобщаются аналогичные утверждения из [9], [12].
Теорема 3. Пусть 0 <
p, q Ј Ґ, a > 0, u є u0 О h(p,q,a). Если F = (u0,
u1,..., un) является системой сопряженных гармонических
функций, то
(i) ||F||p,q,a Ј C||u||p,q,a.
(ii) Условие yaMp(u;y) = o(1) при y ® +0 (y ® +Ґ) равносильно условию
| yaMp(F;y) = o(1) при y ® +0 (соотв. y ® +Ґ). | |
В качестве следствия получаем, что
преобразования Рисса ограниченны также в пространствах Блоха B.
3. Основная сложность
при доказательстве теорем 2 и 3 возникает при малых p. Это объясняется тем, что
при p < (n - 1)/n функция |Сf|p (где f гармонична) не обязана быть
субгармонической, а функция Mp(f;y) - монотонной по y > 0.
Применяя известное разложение Уитни в
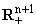 , мы доказываем для h(p,p,a), 0 < p < Ґ максимальную
теорему типа Харди-Литтлвуда, которая позволяет преодолеть указанные трудности.
, мы доказываем для h(p,p,a), 0 < p < Ґ максимальную
теорему типа Харди-Литтлвуда, которая позволяет преодолеть указанные трудности.
Теорема 4. Пусть 0 <
p < Ґ, a >
0, u(x,y) О h(p,p,a). Тогда максимальная функция
| u*(x,y) = |
sup
|
|
м
н
о |
|u(x,h)|; |x - x|2 + (h - y)2 Ј
y2/4 |
ь
э
ю |
, x О Rn, y >
0 | |
удовлетворяет неравенству
| ||u*||p,p,a Ј C(a,p,n)||u||p,p,a . | |
4. В качестве приложений
к теоремам 1-3 дадим характеризацию классов h(p,q,a)
через интегральные представления с использованием пространств Бесова
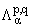 на
Rn. Пусть 1 Ј p,q Ј Ґ, a
> 0 и f(x) - измеримая функция на Rn.
Полунорма Бесова определяется как
на
Rn. Пусть 1 Ј p,q Ј Ґ, a
> 0 и f(x) - измеримая функция на Rn.
Полунорма Бесова определяется как
| ||f||Lap,q = |
м
п
п
н
п
п
о |
|
ж
з
и
|
|
у
хRn
|
|t|-n-aq||Dtk f(x)||qLp(dx)
dt |
ц
ч
ш
|
1/q
|
, | |
|
|
sup
|t| >
0
|
|t|-a||Dtk f(x)||Lp(dx),
| |
| |
| |
где
Dt1 f(x) = f(x + t) - f(x) и Dtk
f(x) = Dt1Dtk-1f(x); k -
целое число, k > a. Существует пригодное для всех
q, 0 < q Ј Ґ
эквивалентное определение (см. [6])
| ||f||Lap,q = ||Dk v||p,q,k-a, | |
где
v = v(x,y) - интеграл Пуассона функции f на
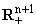 .
.
Теорема 5. Пусть заданы
любые числа 1 Ј p < Ґ, 0 < q Ј Ґ, a > 0. Тогда:
(i) Пространство h(p,q,a) совпадает с множеством
функций u(x,y), представимых в виде
| u(x,y) = |
у
хRn |
DbP(x - t,y) j(t)dt, x
О Rn, y >
0, | |
(2) |
где b (a < b < a + n/p) - произвольное, и
|
j(t) О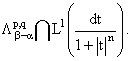
|
(3) |
Вместе с тем, нормы ||u||p,q,a и ||j||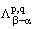 эквивалентны.
эквивалентны.
(ii) Функция j из (2)-(3) выражается через
следующую формулу обращения
| j(x) = |
lim
y®+0
|
D-b
u(x,y), п. в. x
О Rn. | |
(4) |
(iii) Пространство h(p,q,a) совпадает с
множеством функций u(x,y), представимых в виде (2), где b (a < b Ј a + n/p)
- произвольное, и
|
j(t) О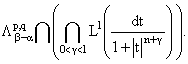
|
Вместе с тем, нормы
||u||p,q,a и ||j||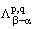 эквивалентны,
и имеет место формула обращения (4).
эквивалентны,
и имеет место формула обращения (4).
Аналогичные представления в случае единичного
круга установлены в [5].
Замечание. Связь между
пространствами Бесова и весовыми классами Aa* Неванлинны-Джрбашяна [13], [14] функций,
голоморфных в единичном круге, установлена Ф. Шамояном [15], [16].
В заключение приведем более простое
интегральное представление для пространства h(2,2,a).
Теорема 6. Пространство h(2,2,a) (a > 0) совпадает с множеством функций u(x,y), представимых
в виде
| u(x,y) = |
у
хRn |
DaP(x - t,y) j(t)
dt, x О
Rn, y >
0, | |
где j(t) О L2(Rn).
Кроме того, функция j может быть выведена из следующей формулы обращения
| j(x) = |
lim
y®+0
|
D-au(x,y), п.
в. x О Rn. | |
Доказательство следует из равенства
h(2,2,a) = Da(h2) (см. теоремы 1 и 2).
Соответствующее представление для функций,
голоморфных в единичном круге, было установлено М.М. Джрбашяном [14].
Ереванский государственный
университет
Институт математики НАН РА
Литература
1. Hardy G. H., Littlewood J. E.
- Math. Zeit. 1932. V. 34, p.
403-439.
2. Hardy G. H.,
Littlewood J. E. - Quart. J. Math. (Oxford). 1941. V. 12. p.
221-256.
3. Flett T. M.
- Proc. London Math. Soc. 1970. V. 20. p.
249-275.
4. Flett T. M.
- J. Math. Anal. Appl. 1972. V. 39. p.
125-158.
5. Аветисян К. Л.
- ДНАН Армении. 1999. Т. 99. N. 4. с.
301-305.
6. Taibleson M.
- J. Math. Mech. 1964. V. 13. p.
407-479.
7. Flett T. M.
- Proc. London Math. Soc. 1970. V. 20. p.
749-768.
8. Bui Huy Qui
- Hiroshima Math. J. 1979. V. 9. p.
245-295.
9. Джрбашян А. Э.
- Изв. АН Арм. ССР. Математика. 1987. Т. 22. N. 4. С.
386-398.
10. Аветисян К. Л.
- ДНАН Армении. 2001. Т. 101. N. 1. С.
20-23.
11. Стейн И., Вейс Г.
Введение в гармонический анализ на евклидовых пространствах,
Мир, М. 1973.
12. Аветисян К. Л.
- ДНАН Армении. 2001. Т. 101. N. 3. С.
211-215.
13. Джрбашян M. M.
- ДАН АрмССР. 1945. Т. 3. N. 1. С.
3-9.
14. Джрбашян M. M.
- Сообщ. Ин-та математики и механики АН Арм ССР. 1948. Вып.
2. С. 3-40.
15. Шамоян Ф. А.
- ДАН АрмССР. 1990. Т. 90. N. 3. С.
99-103.
16. Шамоян Ф. А.
- Мат. заметки. 1992. Т. 52. N. 1. С. 128-140.
![]() верхнее полупространство пространства Rn+1, т.е.
верхнее полупространство пространства Rn+1, т.е.![]() =
Rn × (0, Ґ). Точки этого
полупространства будем представлять как (x,y) = (x1,..., xn,
y), x О Rn, y > 0.
Иногда удобно будет обозначать x0 = y.
=
Rn × (0, Ґ). Точки этого
полупространства будем представлять как (x,y) = (x1,..., xn,
y), x О Rn, y > 0.
Иногда удобно будет обозначать x0 = y. ![]() функции f(x,y) положим
функции f(x,y) положим
![]() ) в верхнем
полупространстве
) в верхнем
полупространстве
![]() состоит из
всех (комплекснозначных) гармонических функций u(x,y) в
состоит из
всех (комплекснозначных) гармонических функций u(x,y) в
![]() , для которых
, для которых ![]() функций f(x,y), для которых конечна
квазинорма (норма при 1 Ј p,q Ј Ґ)
функций f(x,y), для которых конечна
квазинорма (норма при 1 Ј p,q Ј Ґ) ![]() тема дробного
интегродифференцирования изучалась в гораздо меньшей степени. Отметим работы М.
Тейблсона [6], Т. Флетта [7], Буй Хюи Ки [8], А. Э. Джрбашяна [9].
тема дробного
интегродифференцирования изучалась в гораздо меньшей степени. Отметим работы М.
Тейблсона [6], Т. Флетта [7], Буй Хюи Ки [8], А. Э. Джрбашяна [9]. ![]() , введем в рассмотрение оператор
дробного интегродифференцирования Римана-Лиувилля (называемый также потенциалом
Рисса):
, введем в рассмотрение оператор
дробного интегродифференцирования Римана-Лиувилля (называемый также потенциалом
Рисса): ![]() функций с граничными значениями из
BMO(Rn).
функций с граничными значениями из
BMO(Rn). ![]() и удовлетворяющей условию
и удовлетворяющей условию ![]() функции f такой, что F = Сf. Заметим, что в случае n = 1
уравнения (1) переходят в обычные уравнения Коши-Римана. При этом функция
F = u0 + iu1 голоморфна относительно переменной
z = x1 + ix0.
функции f такой, что F = Сf. Заметим, что в случае n = 1
уравнения (1) переходят в обычные уравнения Коши-Римана. При этом функция
F = u0 + iu1 голоморфна относительно переменной
z = x1 + ix0. ![]() , мы доказываем для h(p,p,a), 0 < p < Ґ максимальную
теорему типа Харди-Литтлвуда, которая позволяет преодолеть указанные трудности.
, мы доказываем для h(p,p,a), 0 < p < Ґ максимальную
теорему типа Харди-Литтлвуда, которая позволяет преодолеть указанные трудности. ![]() на
Rn. Пусть 1 Ј p,q Ј Ґ, a
> 0 и f(x) - измеримая функция на Rn.
Полунорма Бесова определяется как
на
Rn. Пусть 1 Ј p,q Ј Ґ, a
> 0 и f(x) - измеримая функция на Rn.
Полунорма Бесова определяется как ![]() .
. 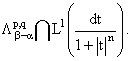
![]() эквивалентны.
эквивалентны. 
![]() эквивалентны,
и имеет место формула обращения (4).
эквивалентны,
и имеет место формула обращения (4).