ФИЗИКА
УДК 539.182
А. М. Ишханян
Решение поляритонной задачи для плавной границы
(Представлено академиком Р. А. Казаряном 12/II 2001)
Поверхностные поляритоны определяются как
локализованные электромагнитные волны, распространяющиеся вдоль границ раздела
различных сред [1,2]. Классическим примером является плазмонный поляритон,
возникающий на границе раздела металл-диэлектрик [1]. Другими важными
примерами являются экситонный [2], магнонный [3] и фононный [4]
поляритоны. С точки зрения физики конденсированных сред поверхностные волны
обусловлены динамикой соответствующих квазичастиц - плазмонов, экситонов,
магнонов, фононов и т. д. Однако с точки зрения электродинамики
сплошных сред, когда длина волны и расстояние распада волны много больше, чем
межатомные расстояния, подобные локализованные волны могут быть рассмотрены
феноменологически, макроскопическими уравнениями Максвелла, через
соответствующие диэлектрические постоянные среды.
В согласии со сказанным под поляритонной
задачей в широком смысле понимается вопрос о существовании локализованных
решений уравнений Максвелла для различных видов пространственных вариаций
(комплексных) тензоров (диэлектрической и/или магнитной) проницаемостей [2].
Под термином "граница" при этом следует
понимать двумерные области пространства - поверхности, в окрестности которых
происходит существенное изменение упомянутых тензоров.
В случае линейных сред (когда D=eE , B=mH и j=sE), свободных от сторонних зарядов, макроскопические
уравнения Максвелла для периодических во времени процессов сводятся к следующей
симметричной относительно перестановки пар (e, E) и
(m, H) системе двух связанных уравнений [5]:
|
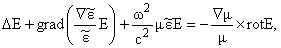 |
(1) |
|
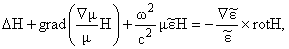 |
(2) |
где комплексная
диэлектрическая проницаемость 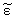 определяется как
определяется как
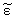 = e - i[(4ps)/(w)].
= e - i[(4ps)/(w)].
Следует
подчеркнуть, что если только одна из проницаемостей испытывает пространственную
вариацию, то, как легко заметить, во-первых, система (1), (2) расщепляется,
т. е. одно из полей E, H может быть определено независимо, а
во-вторых, указанная симметрия относительно перестановки (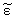 , E ) « (m, H) нарушается.
, E ) « (m, H) нарушается.
Эти очевидные наблюдения влекут за собой
фундаментальную разницу в поведении волн с различной
поляризацией. Математически это выражается в том, что в указанных условиях
уравнения для ТЕ и ТМ мод существенно отличаются.
Например, если среда локально изотропна и
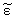 =
=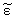 (zў), m=const, то уравнение для ТМ электромагнитной волны будет содержать
дополнительный член, пропорциональный логарифмической производной
диэлектрической проницаемости:
(zў), m=const, то уравнение для ТМ электромагнитной волны будет содержать
дополнительный член, пропорциональный логарифмической производной
диэлектрической проницаемости:
|
| ТЕ мода,
|
®
E
|
= (0, Ey, 0):
DEy + |
w2
c2
|
m |
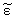 Ey = 0 , Ey = 0 ,
| | |
| |
(3) |
Несмотря на кажущуюся простоту, наличие этого члена, как нетрудно
установить, действительно способно привнести в задачу дополнительную
сингулярность в областях, где
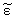 (zў) пересекает ноль. Именно благодаря этой сингулярности
становится возможным существование волн, локализованных в окрестности
одной-единственной границы, т. е. существование поляритонов!
(zў) пересекает ноль. Именно благодаря этой сингулярности
становится возможным существование волн, локализованных в окрестности
одной-единственной границы, т. е. существование поляритонов!
Ввиду сингулярности указанного члена, обычным
подходом в теории поляритонов (и, вообще, ТМ или смешанных волноводных мод)
является приближение резкой границы (бесконечно тонкого переходного слоя), когда
второй член в уравнении (4) отбрасывается, а его учет проводится лишь косвенно,
через граничные условия.
Заметим, что при отбрасывании этого члена
уравнение (4) становится идентичным уравнению (3), которое сводится к виду,
аналогичному одномерному стационарному уравнению Шредингера. Для
последнего, как известно, существует хорошо развитый аппарат специальных
функций, опирающийся на гипергеометрический тип уравнений, имеющих не более трех
особых точек. При сохранении же члена ~ ¶ ( ln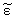 )/¶zў естественно ожидать либо
увеличения числа особых точек, либо увеличения ранга сингулярности этих
точек. Теория подобных уравнений до последнего времени была развита
черезвычайно слабо. Единственными уравнениями, теория которых благодаря
интенсивным усилиям, предпринятым в последнее десятилетие, в настоящий момент
доведена до достаточного для практики уровня, являются пять уравнений класса
Гойна (см. [6] и многочисленные ссылки там). Это наблюдение вселяет
надежду добиться успеха при трактовке поляритонной задачи для плавной границы
через функции Гойна.
)/¶zў естественно ожидать либо
увеличения числа особых точек, либо увеличения ранга сингулярности этих
точек. Теория подобных уравнений до последнего времени была развита
черезвычайно слабо. Единственными уравнениями, теория которых благодаря
интенсивным усилиям, предпринятым в последнее десятилетие, в настоящий момент
доведена до достаточного для практики уровня, являются пять уравнений класса
Гойна (см. [6] и многочисленные ссылки там). Это наблюдение вселяет
надежду добиться успеха при трактовке поляритонной задачи для плавной границы
через функции Гойна.
В настоящей работе мы впервые предпринимаем
подобную попытку. Мы проводим математически строгий учет сингулярного члена
непосредственно в уравнении (4) для модельного профиля вариации диэлектрической
проницаемости по закону гиперболического тангенса.
Как мы убедимся, задача при этом сводится к
каноническому виду общего уравнения Гойна, имеющему четыре простые особые точки.
Мы строим решение исходной задачи в виде степенного ряда, а также приближенное
решение через неполные бета-функции. Далее мы выводим приближенное дисперсионное
соотношение для поляритона, имеющее правильную асимптотику в пределе резкой
границы.
Рассмотрим решения уравнения (4) для ТМ моды,
представляющие собой волны, бегущие вдоль границы, скажем, в направлении
x-координаты: Hy=H(zў)eikxx. Уравнение H(zў) при этом примет вид
|
| Hzўzў - |
Uzў
U
|
Hzў + (l - U)H = 0
. | | |
| |
(5) |
(здесь и далее буквенный индекс
обозначает дифференцирование по соответствующей переменной), где для унификации
записи введены обозначения
|
l =
-kx2 ,
U = -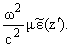 |
(6) |
Следуя методу [7], преобразуем уравнение (5), сохранив его линейность,
заменой зависимой и независимой переменных:
|
| H = j(z)u(z) , zў = |
у
х
|
|
dz
r(z)
|
. | | |
| |
(7) |
В
результате получаем уравнение
|
| uzz = |
ж
з
и
|
2 |
jz
j
|
+ |
rz
r
|
- |
Uz
U
|
|
ц
ч
ш
|
uz + |
й
к
л
|
|
jzz
j
|
+ |
jz
j
|
|
ж
з
и
|
|
rz
r
|
- |
Uz
U
|
|
ц
ч
ш
|
+ |
l-U
r2
|
|
щ
ъ
ы
|
u = 0
. | | |
| |
(8) |
Потребуем, чтобы данное уравнение совпадало с канонической формой общего
уравнения Гойна [6]:
|
| uzz + |
ж
з
и
|
|
g
z
|
+ |
-d
1 - z
|
- |
e
z - a
|
|
ц
ч
ш
|
uz + |
-abz + q
z(1 - z)(z - a)
|
u = 0 ,
| | |
| |
(9) |
где 1 + a + b=g + d + e.
Для этого, очевидно, должно быть:
|
| 2 |
jz
j
|
+ |
rz
r
|
- |
Uz
U
|
= |
g
z
|
+ |
-d
1 - z
|
- |
e
z - a
|
, | | |
| |
(10) |
|
|
ж
з
и
|
|
jz
j
|
|
ц
ч
ш
|
z
|
+ |
jz
j
|
|
ж
з
и
|
|
jz
j
|
+ |
rz
r
|
- |
Uz
U
|
|
ц
ч
ш
|
+ |
l-U
r2
|
= |
-abz + q
z(1 - z)(z - a)
|
u .
| | |
| |
(11) |
Анализ структуры этих уравнений показывает, что следует искать величины
r, j и U в следующем
виде:
|
| j =
za1(1 - z)-a2(z - a)a3 ,
| | |
| |
(12) |
|
| r = |
1
t
|
zn1(1 - z)n2(z - a)n3 ,
| | |
| |
(13) |
|
| U = U0zk1(1 - z)k2(z - a)k3 ,
| | |
| |
(14) |
где t и U0 - произвольные постоянные.
Тогда из уравнения (10) однозначно
определяются параметры g, d, e:
|
| g =
2a1+n1-k1 ,
d = -2a2+ n2-k2 ,
e = 2a3+n3-k3
| | |
| |
(15) |
Наличие же
независимого внешнего параметра l (спектральный
параметр) в уравнении (11) вынуждает наложить на r и U
дополнительные связи:
|
|
lt2
r2
|
~ |
p1
z2
|
+ |
p2
(1-z)2
|
+ |
p3
(z-a)2
|
+ |
q1
z(1-z)
|
+ |
q2
z(z-a)
|
+ |
q3
(1-z)(z-a)
|
,
| | |
| |
(16) |
|
| U = z2n1(1-z)2n2(z-a)2n3×
| |
| × |
ж
з
и
|
|
U1
z2
|
+ |
U2
(1-z)2
|
+ |
U3
(z-a)2
|
+ |
V1
z(1-z)
|
+ |
V2
z(z-a)
|
+ |
V3
(1-z)(z-a)
|
|
ц
ч
ш
|
.
| | |
| |
(17) |
Тогда соответственно определяются параметры a1, 2, 3, q, a, b:
|
| a1(a1+n1-k1-1)+(lp1-U1)t2=0 ,
| |
| a2(a2+n2-k2+1)+(lp2-U2)t2=0 ,
| |
| a3(a3+n3-k3-1)+(lp3-U3)t2=0 ,
| |
| q=-a[a1(a2-n2-k2)+a2(a1+n1-k1)+(lp1-V1)t2]+
| |
| +[a1(a3+n3-k3)+a3(a1+n1-k1)+(lq2-V2)t2] ,
| |
| -ab = [a1(a2-n2-k2)+a2(a1+n1-k1)+(lq1-V1)t2]- | |
| -[a1(a3+n3-k3)+a3(a1+n1-k1)+(lq2-V2)t2]+
| |
| +[a2(a3+n3-k3)+a3(a2+n2-k2)+(lq3-V3)t2]
. | | |
| |
(18) |
Нетрудно увидеть, что дополнительные связи (16), (17) и уравнения (12),
(13), (14) совместны лишь при определенных n1, 2, 3 и k1, 2,
3. Среди допустимых наборов значений этих параметров оказываются лишь
единичные, которые приводят к физически интересным видам профилей
диэлектрической проницаемости. В первую очередь таковыми являются наборы
(n1, n2, n3)=(1, 1, 0) и (k1,
k2, k3)=(0, 0, 1).
Как нетрудно проверить, тогда получается
Преобразование (20) отображает действительную ось zў на отрезок z О [0, 1]. При
этом профиль диэлектрической проницаемости определяет скачок по закону
гиперболического тангенса:
|
|
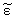 є - є - |
c2
w2m
|
U = - |
c2
w2m
|
|
ж
з
и
|
|
U1+U2
2
|
+ |
U2-U1
2
|
+ |
U1+U2
2
|
+ |
zў-zў0
2t
|
|
ц
ч
ш
|
. | | |
| |
(21) |
Как
видим, ширина переходного слоя определяется параметром t. Параметры задачи теперь явно определяются
спектральным параметром следующим образом:
|
| g =
1+2a1 ,
d = 1-2a2 ,
e = -1
, | | |
| |
(23) |
|
| a =
b = a1-a2 ,
q=a[(a1-a2)2+(a1-a2)]-a1
. | | |
| |
(24) |
Решение уравнения Гойна (9) можно построить в виде степенного ряда:
Для коэффициентов ряда получается
трехчленное рекуррентное соотношение
|
| ann[a(n-1)+ag]-an-1[1+a)(n-1)(n-2)+(g(1+a)+ad+ | |
| +e)(n-1)+q]+an-2[(n-2)(n-3)+(g+d+e)(n-2)+ab) = 0 , n і 0 , | |
| a-2 = a-1 = 0 , a0 = 1 ,
a1 = q/ag,
| | |
| |
(26) |
анализ которого
показывает, что для |a| < 1 ряд (25) сходится, вообще говоря, только на отрезке
z О [0, |a|].
Решение же на отрезке z О [|a|, 1] можно построить аналитическим продолжением, произведя
замену z ® 1-z. Согласно
теории Пуанкаре-Перрона относительно расширенной сходимости [6], существует
значение спектрального параметра l, при котором ряд
(25) сходится всюду на отрезке z О [0, 1]. Это
значение находится из следующего соотношения, заданного в виде бесконечной
дроби:
|
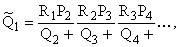 |
(27) |
где Rn,
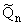 , Pn - суть коэффициенты
рекуррентного соотношения (26) при an, an-1 и an-2
соответственно. Однако можно строго показать, что, к сожалению, данное
значение l не представляет собой собственное значение,
так как решение, соответствующее этому значению, не ограничено при z=1.
, Pn - суть коэффициенты
рекуррентного соотношения (26) при an, an-1 и an-2
соответственно. Однако можно строго показать, что, к сожалению, данное
значение l не представляет собой собственное значение,
так как решение, соответствующее этому значению, не ограничено при z=1.
Однако можно указать простое приближенное
решение исходной задачи, справедливое при малых толщинах переходного
слоя. Это решение нетрудно получить, если заметить, что параметры q и ab в уравнении Гойна (9) квадратично
малы по t. Тогда, переходя к нормальной форме
уравнения (9), можно убедиться, что последний член уравнения Гойна мал и,
следовательно, может быть отброшен. В этом случае решение уравнения (9)
выписывается в замкнутом виде, через неполные бета-функции:
|
| u = C1[Bz(1-2a1, 2a2) - aBz(-2a1, 2a2)] + C2
, | | |
| |
(28) |
где должно быть
выбрано Re[a1] < 0,
Re[a2] > 0.
Для удовлетворения граничного условия
u(z=0)=0 полагаем C2=0. Значение же u(z) при z=1 выражается
через гамма-функции:
|
| u(1) = C1 |
ж
з
и
|
|
a1
a1-a2
|
- a |
ц
ч
ш
|
|
G(-2a1)G(2a2)
G(2(a2-a1))
|
. | | |
| |
(29) |
Следовательно, для
достижения последнего граничного условия u(z=1)=0 должно быть
Как нетрудно
убедиться, последнее условие приводит к формуле для волнового числа поляритона,
справедливой в пределе бесконечно тонкого переходного слоя:
|
| kx2 = |
w2m
c2
|
|
e1e2
e1+e2
|
. | | |
| |
(31) |
Таким образом, мы показали, что задача о поляритоне для плавной границы
с профилем диэлектрической проницаемости, изменяющимся по закону
гиперболического тангенса, сводится к каноническому виду общего уравнения Гойна,
имеющему четыре простые особые точки. Мы вывели дисперсионное соотношение
для волнового числа поляритона и показали, что оно имеет правильную асимптотику
в пределе резкой границы, т. е. когда переходный слой считается
бесконечно тонким.
Примечательно, что ряд других профилей
также может быть изучен с помощью уравнения Гойна. В частности,
один из подобных профилей описывает трехслойную структуру, представляющую
больщой практический интерес [1,2].
Работа была выполнена при поддержке грантов
ISTC No. A-215, RA No. 98-740 и Армянского национального фонда науки и
образования (ANSEF).
Инженерный центр НАН Армении
Литература
1. Raether H. Surface Plasmons. Berlin. Springer-Verlag. 1998; Maradudin A. A. In: Surface Polaritons. Edited by V. M. Agranovich and D. L. Mills,
N. Y. North-Holland. 1982; Yang F., Sambles
J. R., Bradberry G. W. - Phys. Rev. B. 1991.
V. 44. P. 5855.
2. Yang F., Sambles J. R., Bradberry G. W. - Phys. Rev. Lett, V. 64, 559 (1990); A. Brillante, Pockrand I., Philpott M. R., Swalen
J. D. - Chem. Phys. Lett. 1978. V. 57. P. 395.
3. Hickernell R. K., Sarid
D. - Opt. Lett.
1987. V. 12. P. 570.
4. Brion J. J., Wallis
R. F., Harststein A., Burstein E. - Phys. Rev. Lett. 1972. V. 28. P. 1455.
Brion J. J., Wallis R. F., Harststein A., Burstein E.
- Surf. Sci., 1973. V. 34, P. 73 ; Chiu
K. W., Quinn J. J., - Phys.
Rev. B. 1972. V. 5. P. 4707. Lenac
Z., Tomas M. S. -
J. Phys. C. 1983. V. 16. P. 4273.
5. Колесников П. М. Введение в нелинейную
электродинамику: Минск. Наука и
техника. 1971.
6. Ronveaux A., Heun's Differential Equations. London,
Oxford University
Press. 1995.
7. Ishkhanyan A. M. - J. Phys. A. 1997. V. 30. P. 450; Ishkhanyan A. M. - Optics Communications,
2000. V. 176. P. 155. Ishkhanyan
A. M. - J. Phys. A. 2000. V. 33.
P. 5539.
![]() определяется как
определяется как
![]() = e - i[(4ps)/(w)].
= e - i[(4ps)/(w)]. ![]() , E ) « (m, H) нарушается.
, E ) « (m, H) нарушается. ![]() =
=![]() (zў), m=const, то уравнение для ТМ электромагнитной волны будет содержать
дополнительный член, пропорциональный логарифмической производной
диэлектрической проницаемости:
(zў), m=const, то уравнение для ТМ электромагнитной волны будет содержать
дополнительный член, пропорциональный логарифмической производной
диэлектрической проницаемости: ![]() Ey = 0 ,
Ey = 0 ,
![]()
![]() (zў) пересекает ноль. Именно благодаря этой сингулярности
становится возможным существование волн, локализованных в окрестности
одной-единственной границы, т. е. существование поляритонов!
(zў) пересекает ноль. Именно благодаря этой сингулярности
становится возможным существование волн, локализованных в окрестности
одной-единственной границы, т. е. существование поляритонов! ![]() )/¶zў естественно ожидать либо
увеличения числа особых точек, либо увеличения ранга сингулярности этих
точек. Теория подобных уравнений до последнего времени была развита
черезвычайно слабо. Единственными уравнениями, теория которых благодаря
интенсивным усилиям, предпринятым в последнее десятилетие, в настоящий момент
доведена до достаточного для практики уровня, являются пять уравнений класса
Гойна (см. [6] и многочисленные ссылки там). Это наблюдение вселяет
надежду добиться успеха при трактовке поляритонной задачи для плавной границы
через функции Гойна.
)/¶zў естественно ожидать либо
увеличения числа особых точек, либо увеличения ранга сингулярности этих
точек. Теория подобных уравнений до последнего времени была развита
черезвычайно слабо. Единственными уравнениями, теория которых благодаря
интенсивным усилиям, предпринятым в последнее десятилетие, в настоящий момент
доведена до достаточного для практики уровня, являются пять уравнений класса
Гойна (см. [6] и многочисленные ссылки там). Это наблюдение вселяет
надежду добиться успеха при трактовке поляритонной задачи для плавной границы
через функции Гойна.![]()
![]() є -
є -![]()
![]() , Pn - суть коэффициенты
рекуррентного соотношения (26) при an, an-1 и an-2
соответственно. Однако можно строго показать, что, к сожалению, данное
значение l не представляет собой собственное значение,
так как решение, соответствующее этому значению, не ограничено при z=1.
, Pn - суть коэффициенты
рекуррентного соотношения (26) при an, an-1 и an-2
соответственно. Однако можно строго показать, что, к сожалению, данное
значение l не представляет собой собственное значение,
так как решение, соответствующее этому значению, не ограничено при z=1.