МЕХАНИКА
УДК 539.3
И.М. Караханян
Дифракция гармонической волны на упругом полубесконечном
включении в дальнем поле
(Представлено академиком В.С. Саркисяном 4/V 2001)
Работа посвящена изучению задачи
напряженно-деформируемого состояния упругого пространства, содержащего упругое
полубесконечное включение и связанного с дифракцией гармонической волны.
Получены асимптотические формулы для смещения и напряжения упругого
пространства, удобные для анализа в дальнем поле. Отметим, что накопленные в
настоящее время результаты в решениях граничных задач динамической теории
упругости весьма многочисленны.
Достаточно полно изучены законы
распространения упругих волн в сложных средах, позволяющие рассматривать
дифракцию волн на внутренних и поверхностных неоднородностях. В основном
динамические задачи теории упругости для ограниченных тел или тел, содержащих
различного рода неоднородности (включения, трещины и т.п.), сводятся к решению
смешанных задач математической физики, изучение которых связано с достаточно
большими трудностями.
Одной из причин этого является сложность
постановки краевых задач динамической теории упругости для ограниченных тел. С
другой стороны, трудности возникают в связи с спецификой ядер интегральных
уравнений смешанных задач, из-за наличия сильно осциллирующих составляющих ядра
с сохранением свойств сингулярности или других локальных особенностей. Сложность
решения динамических задач диктуется также наличием анизотропии,
неоднородностей, угловых точек в упругой среде и т.д. (см [1-7]).
Интерес к этим задачам особенно возрос в
последнее время, в связи с большой ролью в ряде практических вопросов (колебания
упругих сред, вызванных вибрирующими источниками, сейсмология,
акустикоэлектроника, физическая акустика, вибрационная сейсморазведка, глубинное
зондирование земной коры и т.д.).
Одним из важных методов решения смешанных
задач динамической теории упругости является метод факторизации, в основе
которого лежит факторизация функций и матриц-функций (см. [8-10]). Одновременно
отметим, что задача факторизации является трудной и не всегда разрешимой, о
причинах чего говорилось выше.
Предположим, что упругое включение является
достаточно тонким и находится в упругом полупространстве, упругие свойства
которого не совпадают с соответствующими упругими свойствами пространства. Здесь
рассматривается граничная задача, где граничное условие типа скачка на упругом
включении возникает при дифракции антиплоской гармонической волны в упругом
пространстве, которое находится в антиплоском состоянии (см. [11, 12]).
Граничная задача, рассматриваемая здесь после
отделения временного множителя e-iwt, преобразуется в следующую граничную задачу (1)-(5).
Рассматривается решение стационарного
уравнения Гельмгольца:
| Dv + k2v = d(x - x0)d(y - y0), | |
(1) |
где y0 > 0, |y| > 0, k = В(k) + iБ(k) с В(k) > 0, Б(k) > 0, которое
удовлетворяет следующим граничным условиям:
при x < 0 на включении, условие типа
скачка
|
м
п
н
п
о |
|
|
|
¶v(x, +0)
¶y
|
= m |
¶v(x, -0)
¶y
|
, | | |
| |
(2) |
где n @ 1 - i[(G1b1kd)/(G2)],
m @ 1 - i[(G2b22kd)/(G1b1)].
Здесь bj2 = (
[(c0)/(cj)])2 - 1,
cj2 = [(GJ)/(rj)], а rj и
Gj, (j = 1,2) - плотность и модуль сдвига упругого пространства и
включения, d - толщина включения, c0 -
скорость линейного источника;
при x > 0 условие непрерывности
|
м
п
н
п
о |
|
|
|
¶v(x, +0)
¶y
|
= |
¶v(x, -0)
¶y
|
, | | |
| |
(3) |
кроме того потребуем на
бесконечности выполнение условия типа Зоммерфельда:
|
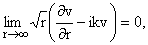
|
(4) |
а также в начале координат около
края включения - условия
|
lim
x®+0
|
v(x, +0) = O(xh), | |
(5) |
где 0 < В(h) Ј
[1/2].
Как было показано в работе [12], разрешимость
граничной задачи (1)-(5) приведена к разрешимости матричного уравнения Винера -
Хопфа:
|
®
v+
|
(a) = L(a) |
®
v-
|
(a) + |
®
m
|
(a), | |
(6) |
что эквивалентно факторизации
матриц-функций L(a) = SN(a), где
S =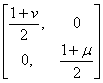 , N(a) =
, N(a) =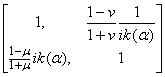 .
.
Здесь k(a) - специально
выбранная ветвь данной двузначной функции.
Ввиду того, что матрица-функция N(a) есть f-циркулянт с f(a) = [((1+n)(1-m))/((1-n)(1+m))](ik(a))2 и алгебра матриц-функций f-циркулянтов есть
комплексная коммутативная банахова алгебра, то, как было показано в [12], в
полосе |Б(a)| < Б(k) она допускает факторизацию
где N-(a) = N+(-a) и N+(a), N-(a) - обратимые аналитические матриц-функции соответственно в
полуплоскостях Б(a) > -Б(k) и Б(a) < Б(k). Это позволяет представить решение граничной задачи в
виде
| v(x,y) = |
м
п
п
п
п
н
п
п
п
п
о
|
|
1
2p
|
|
Ґ+id
у
х
-Ґ+id
|
K+(a)e-iax-g(a)yda + |
1
4i
|
H0(1)(kR) + | |
| + cотр |
1
4i
|
H0(1)(kRў) при y >
0 | |
|
1
2p
|
|
Ґ+id
у
х
-Ґ+id
|
K-(a)e-iax+g(a)yda + cпр |
1
4i
|
H0(1)(kR) при
y <
0, | | |
| |
(8) |
где g(a) = -ik(a), d > 0, r = , R =
, R =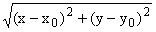 , Rў =
, Rў =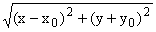 . Здесь K+(a), K-(a) - заданные функции,
H0(1)(*) - соответствующая функция Ханкеля, а
. Здесь K+(a), K-(a) - заданные функции,
H0(1)(*) - соответствующая функция Ханкеля, а
|
м
п
п
п
п
п
н
п
п
п
п
п
о
|
| cотр
@ |
ikd[
c12(c02 - c22)G22 - c22(c02 - c12)G12]
| 2G1G2c1 |
|
_______
Цc02 - c12
|
c22 - ikd[
c12(c02 - c22)G22 - c22(c02 - c12)G12] | |
| |
| cпр
@ |
| 2c1 |
|
_______
Цc02 - c12
|
c22G12G22 |
| 2G1G2c1 |
|
_______
Цc02 - c12
|
c22 - ikd[c12(c02 - c22)G22 - c22(c02 - c12)G12] | |
. | | |
| |
(9) |
Полученное выражение для смещений v(x,y)
позволяет вычислить их во всем пространстве. Однако прямое вычисление этих
интегралов при больших значениях параметров kr, kR, kRў
затрудняется наличием быстро осциллирующих функций в подынтегральных выражениях
(8). Поэтому при таких значениях параметров kr, kR и kRў целесообразно получить асимптотические формулы, удобные для
анализа дальнего поля. Для получения асимптотических формул здесь многократно
используется метод перевала для компонент, входящих в решение v(x,y) граничной
задачи. Для упрощения выкладок методом перевала мы везде ниже будем
рассматривать отсутствие демпфирования, т.е. Б(k) = 0.
Полагая x0 = r0cosj0, y0 = r0sinj0, 0 < j0
< p и x = r cosj, y = r sinj, -p <
j < p, а s = k cos(x), 0 < В(x) < p, мы видим, что функции
M1+(a),
M2+(a), входящие в
K+(a), K-(a) из (8), имеют седловую
точку x = j0 с
простым полюсом kcos(x) = a.
Применяя метод перевала с учетом полюса (см. [8] или [13-15]) к функциям
Mi+(a) (i = 1,2), когда
kr0 ® Ґ, где
r0 =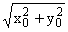 , получаем
, получаем
| Mi+(a) @ |
M < i >
kcosj0 - a
|
+W < i >
(a, j0)eiax0-g(a)y0. | |
(10) |
Здесь величины M < i > и функции W < i > (a, j0) заданы.
Подставляя асимптотические значения функций
Mi+(a) (i = 1,2) в представление для смещения v(x,y) и применяя опять метод перевала в отдельности
по трем параметрам kRў, kR, kr, где:
а) x - x0 = Rўcosyў, y + y0 = Rsinyў, 0 < yў < p, a = kcos(x), 0 < В(x) < p, с седловой точкой x = p-yў, когда kRў ® Ґ;
б) x - x0 = Rcosy, y + y0 = -Rsiny, 0 < y < p, a = kcos(x), 0 < В(x) < p, с седловой точкой x = p-y, когда kR ® Ґ;
в) и два раза по параметру kr, где при 0 <
j < p седловая точка есть
x = p-j, а при -p < j
< 0 седловая точка есть x = p+j, когда kr ® Ґ, получим следующие
асимптотические представления для смещения v(x,y) и напряжения sy(x,y) = G1[(¶v(x,y))/(¶y)] в дальнем поле:
| v(r cosj, r
sinj) @ |
м
п
п
п
п
п
п
п
п
н
п
п
п
п
п
п
п
п
о
|
| cотр |
1
4i
|
H0(1)(kRў)L(j0,yў) + | |
| + |
1
4i
|
H0(1)(kR) + G < 1
> (p-j)H0(1)(kr), | |
|
|
|
|
| cпр |
1
4i
|
H0(1)(kR)L(j0,y) + | |
| + |
1
4i
|
H0(1)(kR){1 - L(j0,y)} + G < 2 > (p+j)H0(1)(kr), | |
|
|
|
| |
| |
(11) |
где L(j0,*) = 1 - H(cosj0 + cos(*)), H(·) - функция Хевисайда, а G < 1 >
(p-j), G < 2 > (p+j) - заданные функции и
| sy(r
cosj, r sinj)
@ |
м
п
п
п
п
п
п
п
п
п
п
п
п
н
п
п
п
п
п
п
п
п
п
п
п
п
о
|
| cотр |
1
4i
|
H0(1)(kRў) |
й
к
л
|
A < 1 > (j0,yў) + |
B < 1 > (j0,yў)
Rў
|
щ
ъ
ы
|
+ | |
| + |
1
4i
|
H0(1)(kR) |
й
к
л
|
C < 1 > (j) + |
D < 1 > (j)
R
|
щ
ъ
ы
|
+, | |
| + |
1
4i
|
H0(1)(kr) |
й
к
л
|
E < 1 > (j0,j) + |
F < 1 > (j0,j)
r
|
щ
ъ
ы
|
| |
|
|
|
|
| cпр |
1
4i
|
H0(1)(kR) |
й
к
л
|
A < 2 > (j0,y) + |
B < 2 > (j0,y)
R
|
щ
ъ
ы
|
+ | |
| + |
1
4i
|
H0(1)(kR) |
й
к
л
|
C < 2 > (j,y) + |
D < 2 > (j,y)
R
|
щ
ъ
ы
|
+, | |
| + |
1
4i
|
H0(1)(kr) |
й
к
л
|
E < 2 > (j0,j) + |
F < 2 > (j0,j)
r
|
щ
ъ
ы
|
| |
|
|
|
| |
| |
(12) |
где функции A < i >
, B < i > , C < i > , D < i >
, E < i > , F < i > , также заданы.
Из представления (11) решения нашей граничной
задачи следует, что значение v(x,y) в точке (x,y) есть:
при y > 0 - сумма следующих трех
слагаемых:
а) член [1/4i]H0(1)(kR)
соответствует падающей упругой волне от линейного источника
(x0,y0);
б) член cотр[1/4i]H0(1)(kRў)L(j0,yў) соответствует отраженной упругой
волне (или от точки (x0,-y0)) с
коэффициентом отражения cотр, заданным соотношением (9);
в) член G < 1 > (p-j)H0(1)(kr) соответствует упругой волне
из начала координат около ребра включения;
при y < 0 - сумма следующих трех
слагаемых:
а) член
[1/4i]H0(1)(kR){1-L(j0,yў)} соответствует падающей упругой волне от линейного
источника (x0,y0);
б) член cпр[1/4i]H0(1)(kR)L(j0,y) соответствует
прошедшей упругой волне от линейного источника (x0,y0) с
коэффициентом прохождения cпр, заданным соотношением (9);
в) член G < 2 > (p+j)H0(1)(kr)
соответствует упругой волне из начала координат около ребра включения.
Аналогичные рассуждение исходя из (12) можно провести и для напряжения.
Автор приносит глубокую благодарность своему
научному руководителю академику В.С. Саркисяну за ценные советы и обсуждения.
Ереванский государственный университет
Литература
1. Ворович И.И., Александров
В.М., Бабешко Б.А. Неклассические смешанные задачи теории
упругости. М. Наука. 1974. 455 с.
2. Гринченко В.Т., Мелешко В.В. Гармонические
колебания и волны в упругих телах. Киев. Наукова думка. 1981. 238 с.
3. Саркисян В.С. Контактные задачи для полуплоскостей и полос с упругими накладками.
Ереван. Изд. ЕГУ. 1983. 256 с.
4. Ворович И.И., Бабешко В.А., Пряхина О.Д. Динамика
массивных тел и резонансные явления в деформируемых средах. М. Научный мир.
1999. 246 с.
5. Ворович
И.И., Бабешко В.А. Динамические смешанные задачи теории
упругости для некласических областей. М. Наука. 1979. 320 с.
6. Морарь Г.А. Метод разрывных решений в механике деформируемых тел. Кишинев. Штиинца.
1984. 130 с.
7. Бреховских
Л.М. Волны в слоистых средах. М. Наука. 1979. 271 с.
8. Нобл Б. Метод Винера-Хопфа. М. ИЛ. 1962. 279 с.
9. Бабешко В.А. Обобщенный метод факторизации в пространственно-динамических смешанных
задачах теории упругости. М. Наука. 1984. 254 с.
10. Litwinchuk G.S., Spitkowski I.M. Factorization of
matrix-funktion. Akademie-Verlag. Berlin. 1987. 372 p.
11.
Саркисян В.С., Караханян И.М. Тезисы конф. 6-го
Всерос. совещания-семинара по инженерно-физическим проблемам новой техники (с
участием стран СНГ). М. МГТУ им Н.Э.Баумана. 2001. С.
54-55.
12. Саркисян В.С., Караханян
И.М. - Уч.зап. ЕГУ. 2001. N 2.
13. Лаврентьев М.А., Шабат Б.В. Методы теории функций
комплексной переменной. М. Наука. 1973. 736 с.
14. Ватсон Г.Н. Теория бесселевых функций. Ч. I. М. ИЛ.
1949. 798 с.
15. Евграфов М.А. Асимптотические оценки и целые функции. М. Наука. 1979. 320 с.
![]()
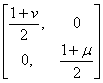 , N(a) =
, N(a) =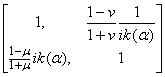 .
. ![]() , R =
, R =![]() , Rў =
, Rў =![]() . Здесь K+(a), K-(a) - заданные функции,
H0(1)(*) - соответствующая функция Ханкеля, а
. Здесь K+(a), K-(a) - заданные функции,
H0(1)(*) - соответствующая функция Ханкеля, а ![]() , получаем
, получаем