УДК 621.2.08

   Система тепловой диагностики гидрогенераторов включает в себя контроль температуры различных конструктивных элементов и прежде всего обмотки и зубцовой зоны статора, тепловое состояние которых обусловлено действием основных электромагнитных нагрузок и в целом определяет надежность и долговечность их эксплуатации [1].
   Даже при номинальном значении указанных нагрузок, не говоря уже о случаях их аномальных превышений в течение любых интервалов времени, в том числе и кратких, возникают и начинают прогрессировать различные необратимые процессы, и в первую очередь термическое старение изоляции обмотки и межлистовой изоляции стали зубцовой зоны статора. Такие процессы развиваются с течением времени непрерывно, вызывая соответствующее ухудшение электрических свойств изоляционных материалов из-за снижения их механических характеристик и химического состава. При этом в разные периоды времени они протекают с различной интенсивностью при сохранении общей тенденции к постепенному ускорению. Процесс ухудшения электрических свойств указанных видов изоляции из-за действия перечисленных причин можно во времени обозначить его началом, отнесенным к исходному нормальному состоянию, в котором совершенно отсутствуют какие-либо разрушения и недопустимые композиционные изменения, и концом, приписываемым состоянию, соответствующему полному разрушению изоляции, абсолютно исключающему функционирование данного конструктивного узла. Таким образом, в интервале времени, ограниченном обозначенными исходным и конечным состояниями изоляции, возникает множество других промежуточных состояний, еще допускающих нормальное функционирование контролируемых узлов с определенным ресурсом безаварийной работы. Теоретически количество промежуточных состояний, каждое из которых может быть определено лингвистически с помощью множества качественных характеристик, стремится к бесконечности, причем переход этих состояний из одного в другое, от исходного к конечному происходит через так называемые "размытые", т.е. нечетко очерченные, границы. Разумеется, говорить о бесконечном множестве состояний не имеет смысла, поскольку для целей диагностики реализация соответствующей информационно-измерительной системы, служащей для контроля указанных состояний, невозможна. Для выхода из затруднительного положения и реализации подобных систем, например, тепловой диагностики статора гидрогенератора, можно воспользоваться экспертными характеристиками градаций указанных состояний, количество которых сводится к разумному минимуму, обусловленному практикой эксплуатации. В качестве примера рассмотрим экспертную классификационную схему возникновения и развития дефектов изоляции статорной обмотки во времени в условиях воздействия нормальных температур, приведенную на рисунке [1].

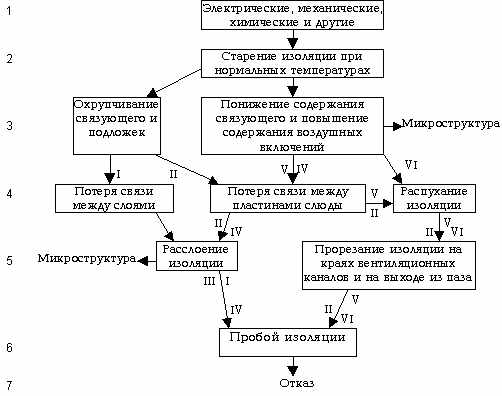
   Здесь изображены временные уровни развития дефектов при нормальных тепловых условиях, начинающихся от ключевого дефекта (уровень 1) и заканчивающихся отказом (уровень 7). При этом события и факты, чередующиеся во времени в виде хронологической последовательности, располагаются на разных уровнях, возрастающее запаздывание которых относительно друг друга отмечено возрастанием номера уровня (числа 1-7). На первом временном уровне в рамке указаны причины возникновения такого ключевого дефекта, как старение изоляции, соответствующего уровню 2. В прямоугольниках других уровней указаны события, являющиеся причинами или следствиями возникновения и развития дефектов, причем все или некоторые из них могут быть использованы в качестве признаков дефектов в случае возможности их выявления с помощью осмотров, наблюдений или испытаний. Стрелки, не замыкающиеся на других прямоугольниках, указывают на события, не входящие в последующие причинно-следственные цепочки развития дефектов и являющиеся только признаками. Однако даже при таком четком разделении на уровни отдельные виды дефектов на одном и том же или разных уровнях определены лингвистическим описанием, эквивалентным его количественной оценке, но лишенным определенной меры с использованием таких нечетких определений градаций, как, например, слабое, весьма заметное, сильное, почти полное охрупчивание и т.д. [2].
   С точки зрения теории нечетных множеств такую меру количественной оценки устанавливают с помощью некоторого числа a, называемого степенью принадлежности и принимающего в закрытом интервале [0,1] любые значения. При этом 0 означает полное отсутствие дефекта, а 1 - присутствие полностью развитого дефекта, что определяется также на основе экспертных оценок. Приняв каждый вид дефекта в качестве признака оценки состояния изоляции и не затрагивая пока вопроса измерения соответствующих им величин, обозначим эти величины через A, B, C, D, E, количественные оценки которых представим в виде степеней принадлежности к вышеуказанному интервалу. Тогда эти величины можно рассмотреть как элементы некоторого конечного множества X={ x₁, x₂, x₃,ј, x_n}, имеющие различные степени принадлежности, фиксированные в отдельных подобластях указанной замкнутой области. Из этого конечного множества можно составить различные нечеткие подмножества A₀ размера n, элементы которых могут иметь различные степени принадлежности a_i, где i = 1,2,ј,n, так что A₀(x_i) = a_i однозначно определит данное нечеткое множество, если для всех значений i будут заданы определенные фиксированные значения a_i. Задача состоит в определении a_i для произвольного A₀ на основе наблюдений, используемых для расчета вероятностных оценок набора некоторых четких множеств уровня a, обозначаемых как A_a. Последние означают такие четкие подмножества множества x, степень принадлежности всех элементов которых не менее чем a, т.е. A_a = {x|A(x) і a, x О X}, причем предполагается, что если a₁ > a₂, то A_a1 Й A_a2. Кроме того, в силу запаздывания различных уровней относительно друг друга во времени значения a для различных сочетаний событий можно считать пропорциональными вероятности наступления совместных событий. При этом исходят из одинаковой вероятности наступления различных отдельных событий, принадлежащих тому или иному уровню при фиксированном количестве последних. Это значит, что при сочетании, состоящем из одного события A, характеризующего уровень 2, при их фиксированном количестве, равном 5, вероятность наступления этого события равна 1/5, а вероятность наступления совместных событий, определяемых сочетанием одного события 2-го уровня и одного из событий 3-го уровня, равна (1/5) · (1/5) = 1/25 и т.д. Поэтому подобласть степени принадлежности отдельного события A определится верхней частью замкнутой области [0,1]. Более конкретно, это утверждение справедливо в зависимости от экспертной оценки общего количества дискретных градаций области [0,1] с одинаковым шагом и от количества частных подобластей в ее верхней части, в которых могут оказаться вероятные значения степеней принадлежности этого события (также на основании экспертной оценки).
   Пусть число градаций (или выборок) M = 25, тогда множество подобластей S  с  одинаковым  шагом  в  области  [0,1]  определится  как  S = [1;0.96;0.92;0.88;ј;0.04], и на основании экспертной оценки значения a для события A могут приобрести значения 1,0.96 и 0.92, т.е. A_1.0 = {A}, A_0.96 = {A} и A_0.92 = {A}. Для наступления совместного события, состоящего из событий A и B, уровневые множества A_a определятся на основе вышеуказанной оценки, допустим, значениями a из 4 подобластей, расположенных левее предыдущих подобластей, т.е. подобласти 0.92, начиная со значения 0.88 до значения 0.76 и т.д. Следует указать только, что состав сочетаний событий полностью определяется переходами от одного уровня к более высоким, обозначенным стрелками, а количество различных значений a, как и прежде, на основе экспертных оценок. В связи с изложенным и в соответствии со схемой, представленной на рисунке, возможны следующие количества элементов уровневых множеств A_a : k = 1,2,3,4 и 5. При этом можно допустить одну из экспертных оценок, при которых, помимо уже отмеченных для первых двух сочетаний, можно указать аналогичные сдвиги для остальных сочетаний. Опять же допустим, что к ним будут отнесены: 6 следующих сдвинутых влево подобластей для сочетания из 3, еще 6 подобластей, следующих влево от предыдущих 6, для сочетания из 4 и такое же количество, тоже сдвинутое влево относительно предыдущих подобластей для сочетания из 5 элементов. Таким образом, получается 25 уровневых множеств:

A1.0={A}, A0.96={A}, A0.92={A}, A0.88={B,A}, A0.84={B,A}, A0.8={B,A}, A0.76={B,A}, A0.72={C,B,A}, A0.68={C,B,A}, A0.64={C,B,A}, A0.6={C,B,A}, A0.56={C,B,A}, A0.52={C,B,A}, A0.48={D,C,B,A}, A0.44={D,C,B,A}, A0.4={D,C,B,A},A0.36={D,C,B,A}, A0.32={D,C,B,A}, A0.28={D,C,B,A}, A0.24={E,D,C,B,A}, A0.2={E,D,C,B,A}, A0.16={E,D,C,B,A}, A0.12={E,D,C,B,A}, A0.08={E,D,C,B,A}, A0.04={E,D,C,B,A}.

   Далее, придерживаясь методики, изложенной в [2], следует подсчитать сумму T_i, представляющих отношения количеств, сопутствующих появлению событий E, D, C, B, A к соответствующему количеству элементов того сочетания, в котором появляется данное событие, т.е.: