|
(1) |
В работе автора [1] для произвольной
непрерывной на [0,+Ґ) функции f(x) введены
квазиполиномы типа Бернштейна - Хаусдорфа
|
(2) |
|
|
(3) |
где sn,k =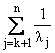 -узлы интерполяции, а контур C охватывает все
особенности подынтегральной
-узлы интерполяции, а контур C охватывает все
особенности подынтегральной
функции. Была установлена равномерная сходимость
квазиполиномов типа (2) к произвольной непрерывной на [0,+Ґ] функции f(x), а также дано обобщение теоремы Вороновской
[2]. Эти квазиполиномы существенно использованы при решении проблемы моментов
[3]. Заметим, что при lj = j, e-x = t из квазиполиномов (2) получаются классические
полиномы С.Н.Бернштейна
|
При
решении аппроксимационной задачи сначала были построены квазиполиномы типа
Бернштейна - Хаусдорфа для функции e-lx l > 0, x О [0,+Ґ], имеющие вид
|
(4) |
и установлена их сходимость к
функции e-lx. Далее
доказана лемма, утверждающая, что при условии (1) на последовательность {lj}
|
и
с использованием теоремы Вейерштрасса осуществлен переход к произвольной
непрерывной функции f(x). к функции elx (l > 0), которая не
ограничена в промежутке [0,+Ґ). Доказательство разобьем
на несколько этапов. Если обе части этого
тождества умножить на [1/(2pi)]exxdx и проинтегрировать по
контуру C, содержащему все особенности подынтегральной функции, то придем к
следующему важному соотношению при l > 0 и lj і 0:
равномерно по x в промежутке [0,A]
при всяком A > 0. exx1dx1
Контур C1,
охватывающий особенности подынтегральной функции в точках x1 = -l, x1 = -mj, j = 0,1,2,ј,n (m0 = 2l), заменим на прямую (-d - iҐ, -d + iҐ), где
0 < d < [(l)/2]. Тогда
exxdx
Таким
образом доказана следующая к неограниченной функции
[1/(tl)] равномерно в промежутке d Ј t Ј 1
при всяком d > 0. Интересен случай l = 1. Тогда
1
они
аппроксимируют функцию [1/t] равномерно в промежутке d
Ј t Ј 1, "d > 0. Кстати, в этом частном
случае сходимость можно доказать проще. Действительно, в выражении
rn*(t;1) сделаем замену переменной x - 1 = x1, dx = dx1. Тогда
t-x1dx1
где
контур C1 охватывает особенности подынтегральной функции в точках
x1 = 0, -1, -2, ј - (n + 1).
Известно, что t-x1dx1
t-x1dx1
Государственный инженерный университет
Армении
1. Багиян Р.А. - ДАН АрмССР. 1975. Т.61. N3. С.129-136.
Bn[ elx] =
n
е
k=0
м
н
о
n
Х
j=k+1
ж
з
и 1 +
l
ljц
ч
ш ь
э
ю wn,k(x) (5)
где
1
x - l=
n
е
k=0
n
Х
j=k+1 (lj + l)
n
Х
j=k (x + lj) + rn(x,l),
rn(x,l) =
n
Х
j=0 (lj + l)
(x - l)
n
Х
j=0 (x + lj) .
где
elx =
n
е
k=0
м
н
о
n
Х
j=k+1
ж
з
и 1 +
l
ljц
ч
ш ь
э
ю wn,k(x) + rn(x;l), (6)
а контур C охватывает особенности
подынтегральной функции в точках l и -lj, j = 0, 1, 2, ј, n.

(7)
Требуется доказать, что
lim
n®Ґ rn(x;l) = 0 (8)
Тогда
m0 = 2l,
lim
j®Ґ mj = +Ґ,
Ґ
е
j=1
1
mj=
Ґ
е
j=1
1
lj + 2l= +Ґ.
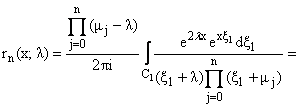
й
к
л
n
Х
j=0 (1 -
l
mj)
щ
ъ
ы
e2lx
2pi
у
х
C1
(x1 + l)
n
Х
j=0 (1 +
x1
mj) .
где
rn(x;l) = Pn(l) · Qn(x;l),
Далее устанавливаются
следующие оценки:
Pn(l) =
n
Х
j=0
ж
з
и
1 -
l
mjц
ч
ш
Qn(x;l) =
e2lx
2pi
d+iҐ
у
х
d-iҐ
(x + l)
n
Х
j=0
ж
з
и 1 +
x
miц
ч
ш
.
где
B(l;d,x) - постоянная, не
зависящая от n. Итак, будем иметь
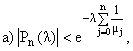
б) |Qn(x;l)| <
B(l,d,x) ![]()
Так
как d < [(l)/2], то при
n ® Ґ за счет расходимости ряда
|rn(x;l)| = |Pn(l) · Qn(x;l)| <
<
![]() B(l,d,x)
B(l,d,x)![]() <
B*(l;d,x)
<
B*(l;d,x)![]() .
.![]() получим
получим
lim
n®Ґ rn(x;l) = 0.
равномерно
по x О [0,A] при всяком A > 0.
lim
n®Ґ Bn[elx] =
lim
n®Ґ
n
е
k=0
м
н
о
n
Х
j=k+1
ж
з
и 1 +
l
ljц
ч
ш ь
э
ю wn,k(x) = elx
3. Рассмотрим теперь частные случаи. Приняв в
соотношении (6) lj = j, e-x = t, 0 < t Ј 1, получим
где
1
tl=
n
е
k=0
м
н
о
n
Х
j=k+1
ж
з
и 1 +
l
jц
ч
ш ь
э
ю Cnk tk(1 - t)n-k + rn(-ln t; l), l >
0,
В
силу доказанной теоремы

и имеем сходимость
аналогов полиномов С.Н.Бернштейна
lim
n®Ґ rn*(t; l) =
lim
n®Ґ rn(-ln t, l) = 0, 0 <
t Ј 1, l >
0.
n
е
k=0
м
н
о
n
Х
j=k+1
ж
з
и 1 +
l
jц
ч
ш ь
э
ю Cnk tk(1 - t)n-k,
l > 0 (9)
и
полиномы (9) будут иметь вид

n
е
k=0
м
н
о
n
Х
j=k+1
ж
з
и
1 +
1
jц
ч
ш
ь
э
ю
Cnk tk(1 - t)n-k =
=
n
е
k=0
k+1
n+1Cnk tk(1 - t)n-k;

=
n!t-1
2pi
у
х
C1
x1
n+1
Х
k=1 (x1 + k) ,
Следовательно,
(1 - t)n =
n!
2pi
у
х
C1
x1
n
Х
k=1 (x1 + k) .
Отсюда при t О [d;1], d
> 0
rn*(t;1) =
t-1(n + 1)!
(n + 1)2pi
у
х
C1
x1
n+1
Х
k=1 (x1 + k) =
t-1(1 - t)n+1
n + 1.
что и требовалось.
lim
n®Ґ rn*(t;1) =
lim
n®Ґ
t-1(1 - t)n+1
n + 1= 0,
2. Багиян Р.А. - ДАН Армении. 1995. Т.96. N2-4. С.15-19.
3. Багиян Р.А. - Изв. АН АрмССР. Математика. 1991. Т.26. N1. С. 324-342.
