МАТЕМАТИКА
УДК 517. 57
К. Л. Аветисян
Ограниченные проекторы на гармонических пространствах со
смешанной нормой
(Представлено академиком Н.У Аракеляном 23/II 2001)
1. В настоящей заметке рассмотрены известные
пространства h(p,q,a) гармонических в полупространстве
функций со смешанной нормой. Анонсированы некоторые результаты, относящиеся к
интегральным представлениям и ограниченным проекторам в указанных пространствах.
Пусть Rn -
n-мерное евклидово пространство, и пусть x = (x1,..., xn)
О Rn, |x|2
= x12 + ј + xn2,
dx = dx1јdxn. Обозначим через
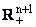 верхнее полупространство
пространства Rn+1, т.е.
верхнее полупространство
пространства Rn+1, т.е.
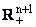 =
Rn × (0,Ґ). Точки этого
полупространства будем представлять как (x,y) = (x1,..., xn,
y), x О Rn, y >
0. Иногда удобно будет обозначать x0 = y.
=
Rn × (0,Ґ). Точки этого
полупространства будем представлять как (x,y) = (x1,..., xn,
y), x О Rn, y >
0. Иногда удобно будет обозначать x0 = y.
Для измеримой в
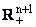 функции f(x,y) положим
функции f(x,y) положим
| Mp(f;y) = ||f||Lp(Rn, dx),
y > 0, 0
< p Ј Ґ. | |
Пространство
Харди hp(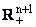 ) в верхнем
полупространстве
) в верхнем
полупространстве
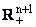 состоит из
всех (комплекснозначных) гармонических функций u(x,y) в
состоит из
всех (комплекснозначных) гармонических функций u(x,y) в
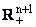 , для которых
, для которых
| ||u||hp = |
sup
y > 0
|
Mp(u;y) < +Ґ. | |
Введем
в рассмотрение квазинормированное пространство L(p,q,a) (0 < p,q Ј
Ґ, a > 0), состоящее из тех
измеримых в
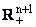 функций f(x,y), для
которых конечна квазинорма (норма при 1 Ј p,q Ј Ґ)
функций f(x,y), для
которых конечна квазинорма (норма при 1 Ј p,q Ј Ґ)
| ||f||p,q,a = |
м
п
п
н
п
п
о |
|
|
ж
и
|
у
х
|
+Ґ
0
|
yaq-1Mpq(f;y)
dy |
ц
ш
|
1/q
|
, | |
|
|
ж
и
|
ess |
sup
y >
0
|
ц
ш
|
ya Mp(f;y),
| |
| |
| |
Пусть h(p,q,a) - гармоническое подпространство пространства L(p,q,a). Гармонические пространства h(p,q,a) со смешанной нормой в полупространстве исследованы
несколькими авторами. Среди них отметим М. Тейблсона [1], Т. Флетта [2,3], Буй
Хюи Ки [4], Ф. Ричи и М. Тейблсона [5], А. Э. Джрбашяна [6]. При p = q < Ґ пространства h(p,q,a) иногда
называют весовыми пространствами Бергмана, хотя сам Бергман [7,8] начиная с 1929
г. изучал лишь функции, интегрируемые с квадратом без веса, т.е. гильбертово
пространство h(2,2,1/2). В работах М. М. Джрбашяна [9,10] введены весовые классы
h(p,p,a) (1 Ј p <
Ґ) и получены их интегральные представления для
функций, голоморфных в единичном круге. Тем не менее, ряд важных свойств классов
h(p,q,a), относящихся к вопросам вложения и дробного
интегродифференцирования, ранее установлен Харди и Литтлвудом [11,12].
2. Для функции f(x,y), измеримой и
комплекснозначной в
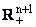 , введем в
рассмотрение оператор дробного интегродифференцирования Римана-Лиувилля
(называемый также потенциалом Рисса):
, введем в
рассмотрение оператор дробного интегродифференцирования Римана-Лиувилля
(называемый также потенциалом Рисса):
| D-af(x,y) = |
1
G(a)
|
|
у
х |
+Ґ
0
|
sa-1f(x,y + s)ds, | |
| D0
f = f, Daf(x,y) = (-1)mD-(m-a) |
¶m
¶ym
|
f(x,y), | |
где a > 0, а m- целое, m - 1 < a Ј m.
В верхнем полупространстве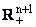 ядро Пуассона P є P0 и сопряженные ядра Пуассона
Pj (1 Ј j Ј n)
определяются формулами
ядро Пуассона P є P0 и сопряженные ядра Пуассона
Pj (1 Ј j Ј n)
определяются формулами
| Pj(x,y) = kn |
xj
(|x|2 + y2)(n+1)/2
|
, kn = |
p(n+1)/2
|
, 0 Ј j Ј
n. | |
Символы C(a,b,...), ca и т.п. обозначают различные положительные постоянные,
зависящие только от указанных индексов a, b,.... Пусть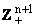 - множество всех мультииндексов l = (l1,..., ln,
ln+1) с неотрицательными координатами lj О Z+ и пусть |l| = l1 + ј + ln + ln+1 и
- множество всех мультииндексов l = (l1,..., ln,
ln+1) с неотрицательными координатами lj О Z+ и пусть |l| = l1 + ј + ln + ln+1 и
| ¶l = |
ж
з
и |
¶
¶x1
|
ц
ч
ш |
l1
|
ј |
ж
з
и |
¶
¶xn
|
ц
ч
ш |
ln
|
|
ж
з
и |
¶
¶y
|
ц
ч
ш |
ln+1
|
. | |
3. Следующая лемма о производных ядер
Пуассона доказывается прямой оценкой.
Лемма 1. Если a > 0, l О
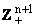 , [n/(n+a)] < p Ј Ґ, то для каждого j, 0 Ј j Ј n, справедливы оценки
, [n/(n+a)] < p Ј Ґ, то для каждого j, 0 Ј j Ј n, справедливы оценки
|
| |DaPj(x,y)| Ј C(a,n) |
1
(|x| + y)a+n
|
, | |
|
| |¶lPj(x,y)| Ј C(l,n) |
1
(|x| + y)|l|+n
|
, | |
| |
| |
|
| Mp(DaPj;y) Ј C(a,n,p) |
1
ya+n-n/p
|
, | |
|
| Mp(¶lPj;y) Ј C(l,n,p) |
1
y|l|+n-n/p
|
, | |
| |
| |
Лемма 2. При 0
< p Ј p0 Ј Ґ, 0 < q Ј q0
Ј Ґ, a + n / p = a0 + n / p0
имеют место следующие непрерывные вложения
| ||u||p0,q0,a0 Ј C
||u||p,q,a, | |
где
C = C(p,q,a,p0,q0,n). Более того,
если u(x,y) О h(p,q,a) с q
< Ґ, то
| yaMp(u;y) = o(1) при y ® +0 и y ® +Ґ. | |
В полуплоскости (т.е. при n = 1) лемма 2
доказана Ричи и Тейблсоном [5]. Вложение h(p,q,a) М h(p,Ґ,a)
из леммы 2 приводит к следующему полезному свойству классов h(p,q,a).
Лемма 3. Пусть u(x,y)
О h(p,q,a) (0 < p,q
Ј Ґ, a > 0) , uh(x,y) = u(x,y + h). Тогда
квазинорма ||uh||p,q,a "почти" возрастает по h
і 0, т.е.
| ||uh1||p,q,a Ј C(p,q,a,n) ||uh2||p,q,a, h1 > h2 і
0. | |
4. Для функции u(x,y), гармонической в
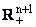 и удовлетворяющей условию
и удовлетворяющей условию
| u(x,y) = O |
ж
з
и |
1
yd
|
ц
ч
ш |
, y ® +Ґ, d
> 0, | |
преобразования Рисса
определяются как
| uj(x,y) = (Rju)(x,y) = - |
у
х |
+Ґ
y
|
|
¶u(x,h)
¶xj
|
dh, 1 Ј j Ј
n. | |
Вектор-функция
F = (u0,u1,...,un), u = u0,
является системой Рисса сопряженных гармонических функций (см., например, [13]),
т.е. функции uj удовлетворяют обобщенным уравнениям Коши-Римана
|
n
е
j=0
|
|
¶uj
¶xj
|
= 0, |
¶uj
¶xk
|
= |
¶uk
¶xj
|
, 0 Ј j,k Ј
n. | |
(1) |
Эти уравнения равносильны
существованию гармонической в
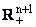 функции f такой, что F = С f. Заметим, что в случае n = 1
уравнения (1) переходят в обычные уравнения Коши-Римана. При этом функция
F = u0 + iu1 голоморфна относительно переменной
z = x1 + ix0.
функции f такой, что F = С f. Заметим, что в случае n = 1
уравнения (1) переходят в обычные уравнения Коши-Римана. При этом функция
F = u0 + iu1 голоморфна относительно переменной
z = x1 + ix0.
Теорема 1. Пусть a > 0 и u є u0 О h(p,q,a). Пусть также выполнены
условия 0 < p,q Ј Ґ, b > max{a + n / p - n, a} либо условия p = 1, 0 < q Ј
1, b і a. Тогда имеют место следующие интегральные представления (0
Ј j Ј n)
uj(x,y) =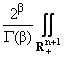 u(x,h) DbPj(x - x,y + h) hb-1dxdh, x О Rn, y > 0. u(x,h) DbPj(x - x,y + h) hb-1dxdh, x О Rn, y > 0.
| |
(2) |
Как видим, дробные производные ядра Пуассона
и сопряженных ядер Пуассона обладают воспроизводящим свойством. Указанное
свойство для ядра DbP0 было впервые замечено М.М. Джрбашяном
([14], с. 596) применительно к функциям, голоморфным и гармоническим в
замыкании единичного круга.
Для j = 0 и целых b
представление (2) было доказано Ричи и Тейблсоном [5] при n = 1 и А.Э. Джрбашяном
[6] при n і 1 и p = q < Ґ.
5. Определим семейство операторов (a > 0, 0 Ј j Ј n)
Ta,j(f)(x,y) =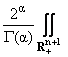 f(x,h) DaPj(x - x,y + h) ha-1dxdh. f(x,h) DaPj(x - x,y + h) ha-1dxdh. | |
В
следующей теореме рассмотрен вопрос о гармонической проекции, осуществляемой
этими операторами.
Теорема 2. Если 1 Ј p,q Ј Ґ,
b > a > 0, 0 Ј j Ј n, то оператор Tb,j является ограниченным проектором из L(p,q,a) на h(p,q,a), т.е.
| ||Tb,jf||p,q,a Ј C||f||p,q,a " f О L(p,q,a). | |
Для j = 0, 1 Ј p = q
< Ґ и целых b теорема 2
доказана в [6].
Далее, естественно встает вопрос об
ограниченности оператора гармонического сопряжения (т.е. преобразований Рисса
Rj) в пространствах h(p,q,a). Поскольку
представление (2) можно переписать в виде uj = Tb,j(u), то из теорем 1 и 2 немедленно вытекает
Следствие. При 1 Ј p,q Ј Ґ, a > 0 преобразования
Рисса Rj (1 Ј j Ј n) ограниченны на h(p,q,a),
т.е.
| ||uj
||p,q,a
Ј C||u||p,q,a " u О h(p,q,a). | |
На самом деле преобразования Рисса
ограниченны на h(p,q,a) при всех 0 < p,q Ј Ґ. Однако доказательство этого
факта требует привлечения дополнительных рассуждений.
Ереванский государственный
университет
Институт математики НАН Армении
Литература
1. Taibleson M. J.-Math.
Mech. 1964. V. 13. P. 407-479.
2. Flett T. M. - Proc. London Math. Soc. 1970. V. 20.
P. 249-275.
3. Flett T. M.
- Proc. London Math. Soc. 1970. V. 20. P.
749-768.
4. Bui Huy Qui
- Hiroshima Math. J. 1979. V. 9. P.
245-295.
5. Ricci F., Taibleson
M. - Annali Scuola Nor. Sup.-Pisa, Ser. IV. 1983 V. 10. P.
1-54.
6. Джрбашян А. Э.
- Изв. АН Арм ССР. Математика. 1987. T. 22. N. 4. С.
386-398.
7. Bergman S.
- Math. Zeit. 1929. V. 29. P.
641-677.
8. Bergman S.
The kernel function and conformal mapping. Math. Surveys,
No. 5. N.Y. 1950.
9. Джрбашян M.
M. - ДАН АрмССР, 1945. T. 3. No. 1. С.
3-9.
10. Джрбашян М. М. -
Сообщ. Ин-та математики и механики АН Арм ССР. 1948. Вып. 2. С.
3-40.
11. Hardy G. H., Littlewood J.
E. - Math. Zeit. 1932. V. 34. P.
403-439.
12. Hardy G. H., Littlewood J.
E. - Quart. J. Math. (Oxford). 1941. V. 12. P.
221-256.
13. Стейн И., Вейс Г. Введение в гармонический анализ на евклидовых пространствах. М. Мир.
1973.
14. Джрбашян М. М. Интегральные преобразования и представления функций в комплексной
области. М. Наука. 1966.
![]() ) в верхнем
полупространстве
) в верхнем
полупространстве
![]() состоит из
всех (комплекснозначных) гармонических функций u(x,y) в
состоит из
всех (комплекснозначных) гармонических функций u(x,y) в
![]() , для которых
, для которых ![]() верхнее полупространство
пространства Rn+1, т.е.
верхнее полупространство
пространства Rn+1, т.е. ![]() =
Rn × (0,Ґ). Точки этого
полупространства будем представлять как (x,y) = (x1,..., xn,
y), x О Rn, y >
0. Иногда удобно будет обозначать x0 = y.
=
Rn × (0,Ґ). Точки этого
полупространства будем представлять как (x,y) = (x1,..., xn,
y), x О Rn, y >
0. Иногда удобно будет обозначать x0 = y.![]() функции f(x,y) положим
функции f(x,y) положим ![]() ) в верхнем
полупространстве
) в верхнем
полупространстве
![]() состоит из
всех (комплекснозначных) гармонических функций u(x,y) в
состоит из
всех (комплекснозначных) гармонических функций u(x,y) в
![]() , для которых
, для которых ![]() функций f(x,y), для
которых конечна квазинорма (норма при 1 Ј p,q Ј Ґ)
функций f(x,y), для
которых конечна квазинорма (норма при 1 Ј p,q Ј Ґ) ![]() , введем в
рассмотрение оператор дробного интегродифференцирования Римана-Лиувилля
(называемый также потенциалом Рисса):
, введем в
рассмотрение оператор дробного интегродифференцирования Римана-Лиувилля
(называемый также потенциалом Рисса): ![]() ядро Пуассона P є P0 и сопряженные ядра Пуассона
Pj (1 Ј j Ј n)
определяются формулами
ядро Пуассона P є P0 и сопряженные ядра Пуассона
Pj (1 Ј j Ј n)
определяются формулами ![]() - множество всех мультииндексов l = (l1,..., ln,
ln+1) с неотрицательными координатами lj О Z+ и пусть |l| = l1 + ј + ln + ln+1 и
- множество всех мультииндексов l = (l1,..., ln,
ln+1) с неотрицательными координатами lj О Z+ и пусть |l| = l1 + ј + ln + ln+1 и ![]() , [n/(n+a)] < p Ј Ґ, то для каждого j, 0 Ј j Ј n, справедливы оценки
, [n/(n+a)] < p Ј Ґ, то для каждого j, 0 Ј j Ј n, справедливы оценки ![]() и удовлетворяющей условию
и удовлетворяющей условию ![]() функции f такой, что F = С f. Заметим, что в случае n = 1
уравнения (1) переходят в обычные уравнения Коши-Римана. При этом функция
F = u0 + iu1 голоморфна относительно переменной
z = x1 + ix0.
функции f такой, что F = С f. Заметим, что в случае n = 1
уравнения (1) переходят в обычные уравнения Коши-Римана. При этом функция
F = u0 + iu1 голоморфна относительно переменной
z = x1 + ix0. 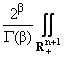 u(x,h) DbPj(x - x,y + h) hb-1dxdh, x О Rn, y > 0.
u(x,h) DbPj(x - x,y + h) hb-1dxdh, x О Rn, y > 0.
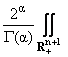 f(x,h) DaPj(x - x,y + h) ha-1dxdh.
f(x,h) DaPj(x - x,y + h) ha-1dxdh.