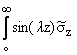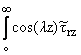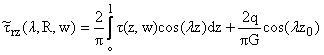ТЕОРИЯ УПРУГОСТИ
УДК 539.3; 534.1
Академик Б. Л. Абрамян
О сдвиговых колебаниях жесткой кольцевой
облицовки,
установленной на конечном слабом участке
поверхности
цилиндрической полости
(Представлено 12/IX 2000)
Рассматриваются сдвиговые осесимметричные
колебания жесткой кольцевой облицовки, установленной со сцеплением на конечном
участке поверхности цилиндрической полости в однородном неограниченном упругом
пространстве. Такие колебания возникают под действием динамической нагрузки на
трассах подземного транспорта. Дается способ определения амплитуды
колебаний.
1. Пусть жесткая весомая
кольцевая облицовка конечной ширины установлена на цилиндрической поверхности
полости со сцеплением и под действием стационарной динамической нагрузки
совершает осевые, осесимметричные колебания с амплитудой g. Полагаем, что облицовка других движений не
совершает. Тогда граничные условия для решения динамической контактной
задачи для однородного упругого пространства с круглой цилиндрической полостью с
жесткой облицовкой на конечном участке полости длиною 2l можно брать в виде
|
|
_
ur
|
|r=R = |
_
uz
|
|r=R - geiwt = 0
(-l < z <
l) | |
|
_
sr
|
|r=R = |
_
trz
|
|r= R - |
q
G
|
d(z - z0)eiwt = 0
(l < |z|,z0 < Ґ) | | |
ь
п
п
э
п
п
ю |
| |
(1.1) |
|
_
ur
|
(r,o,t) = |
_
sz
|
(r,o,t) = 0 (R Ј r < Ґ) | |
(1.2) |
где
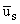 = us(r,z)eiwt (s = r,z) -
перемещения;
= us(r,z)eiwt (s = r,z) -
перемещения;
 = ss(r,z)eiwt,
= ss(r,z)eiwt,
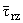 = trz(r,z)eiwt - напряжения в
цилиндрической системе координат; g - величина
амплитуды колебаний облицовки, которую в условиях (1.1) считаем известной, q -
интенсивность динамической нагрузки, z0 - расстояние приложенной,
осесимметричной динамической нагрузки от облицовки, 2l - ширина облицовки, R -
радиус цилиндрической полости, w - частотный параметр, G - модуль сдвига
упругого пространства.
= trz(r,z)eiwt - напряжения в
цилиндрической системе координат; g - величина
амплитуды колебаний облицовки, которую в условиях (1.1) считаем известной, q -
интенсивность динамической нагрузки, z0 - расстояние приложенной,
осесимметричной динамической нагрузки от облицовки, 2l - ширина облицовки, R -
радиус цилиндрической полости, w - частотный параметр, G - модуль сдвига
упругого пространства.
Условия (1.2) являются условиями
антисимметричности деформации упругого пространства относительно срединной
плоскости z = 0.
Решение задачи с условиями (1.1) и (1.2)
строится при помощи потенциалов Г. Гельмгольца [1, 2], которые для решения
осесимметричной задачи берутся в виде интегралов Фурье в следующем виде:
|
| j(r,z) = |
Ґ
у
х
°
|
As(l)K0(ma r)sin(lz)dl | |
| ms = |
Ц
|
l2 - s2w2
|
,
s = a,b, | |
| y(r,z) = |
Ґ
у
х
°
|
Ac(l)K1(mbr)cos(lz)dl, | | |
| |
(1.3) |
где F(r,z,t) = j(r,z)eiwt,
Y(r,z,t) = y(r,z)eiwt - функции Г. Гельмгольца. Уравнения,
которым удовлетворяют эти функции и представления компонентов перемещения и
напряжений при помощи этих функций, приводятся в работах [1,2].
Представления функций F и Y в виде (1.3) обеспечивают единственность и ограниченность
решения задачи с условиями (1.1) и (1.2) во всей области, занимаемой
неограниченным однородным упругим пространством с цилиндрической полостью и
облицовкой на конечном участке [3,4].
Представляя
компоненты перемещения и напряжений в виде интегралов Фурье и удовлетворив
условиям (1.1) и (1.2), получим систему парных интегральных уравнений,
содержащих тригонометрические функции
|
|
Ґ
у
х
0
|
sin(lz)[Ac(l)lK1(mbR) - As(l)maK1(maR)]dl = 0 | |
|
|
|
Ґ
у
х
0
|
cos(lz)[Ac(l)lK0(mbR) - Ac(l)mbK0(mbR)]dl = g | | |
ь
п
п
э
п
п
ю |
| |
(1.4) |
|
|
Ґ
у
х
0
|
sin(lz){As(l)[(2l2 - b2w2)
K0(maR) + |
2ma
R
|
K1(maR)] - | |
| - Ac(l)2l[ |
K1mbR
R
|
+ mbK0(mbR)]}dl =
0 (l
< z, z0) < Ґ) | |
|
Ґ
у
х
0
|
cos(lz)[Ac(l)(2l2 - b2w2)
K1(mbR) - 2lmaAs(l) K1(maR)]dl = |
q
G
|
s(z - z0) | | |
ь
п
п
п
э
п
п
п
ю
|
| |
(1.5) |
Для решения системы уравнений (1.4) и (1.5) вводятся
обозначения
|
|
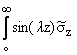 (l,R,w)dl = (l,R,w)dl = |
м
п
н
п
о |
|
| |
|
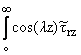 (l,R,w)dl = (l,R,w)dl = |
м
п
н
п
о |
|
| | |
ь
п
п
п
п
э
п
п
п
п
ю
|
| |
(1.6) |
где
|
|
 (l,R,w)As(l)[(2l2 - b2w2)K0(maR) + (l,R,w)As(l)[(2l2 - b2w2)K0(maR) + |
2ma
R
|
K1(maR)] - | |
| - Ac(l)2l[ |
K1(mbR)
R
|
+ mbK0(mbR)] | |
|
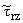 (l,R,w) = Ac(l)(2l2 - b2w2)K1(mbR) - 2lmaAs(l) K1(maR) (l,R,w) = Ac(l)(2l2 - b2w2)K1(mbR) - 2lmaAs(l) K1(maR) | | |
ь
п
п
п
э
п
п
п
ю
|
| |
(1.7) |
s(z,w) и
t(z,w) - безразмерные контактные напряжения, возникшие
под облицовкой.
Из (1.6) будем иметь
значения
Определив при
помощи соотношений (1.7) и (1.8) коэффициенты As(l) и Ac(l) через
контактные напряжения s(z,w) и t(z,w) и подставив полученные значения для них в равенства
(1.4), приведем эти уравнения к виду системы сингулярных интегральных уравнений
первого рода, содержащих контактные напряжения
|
|
l
у
х
°
|
s(t,w)M11(z,t,w)dt + |
l
у
х
°
|
t(t,w)M12(z,t,w)dt + |
q
G
|
M12(z,z0,w) = 0 | |
|
|
|
l
у
х
°
|
s(t,w)M21(z,t,w)dt + |
l
у
х
°
|
t(t,w)M22(z,t,w)dt + |
q
G
|
M22(z,z0,w) = gp | | |
ь
п
п
п
э
п
п
п
ю
|
| |
(1.9) |
Коэффициенты
Mij содержат геометрические и физические параметры упругого
однородного пространства с полостью и облицовкой на конечном участке
полости.
Если из второго уравнения (1.9) исключить
неизвестную величину g при помощи равенства
| g = |
4pRg
Qw2
|
|
l
у
х
°
|
t(t,w)dt, | |
(1.10) |
которым представляется условие
динамического равновесия движений (в (1.10)) Q - вес облицовки), уравнения (1.9)
представятся в виде, в котором контактные напряжения не будут зависеть от
амплитудной величины g. Такие
системы, подобные (1.9), исследовались в работах В.А. Бабешко [5-7] и др. После
решения системы интегральных уравнений вида (1.9), не содержащей величины g, это амплитудное значение можно определить непосредственно
из равенства (1.10). Однако для определения амплитудного значения колебаний для
абсолютно жесткой облицовки можно пользоваться также равенством
| g = |
1
p
|
[ |
l
у
х
°
|
s(t,w)M21(o,t,w)dt + |
l
у
х
°
|
t(t,w)M22(0,t,w)dt + M22(0,z0,w)]. | |
(1.11) |
2. Систему
интегральных уравнений вида (1.9) для рассмотренной задачи можно представить в
виде
|
l
у
х
°
|
s(t,w)ln |
к
к
к |
t + z
t - z
|
к
к
к |
dt = Fs
(z), |
l
у
х
°
|
t(t,w)ln |
к
к
к |
t2 - z2
t2
|
к
к
к |
dt = Ft(z) (o Ј z < l), | |
(2.1) |
где использованы обозначения
|
| Fs(z) = |
l
у
х
°
|
s(r,w)dr[2 |
Ґ
у
х
°
|
|
sin(lr)sin(lz)
l
|
dl - M11(z,r,w)] - | |
| - |
l
у
х
°
|
t(r,w)M21(z,r,w)dr - |
q
G
|
M12(z,z0,w), | |
| Ft(z) = - |
l
у
х
°
|
s(r,w)M21(z,r,w)dr + |
l
у
х
°
|
t(r,w)dr[2 |
Ґ
у
х
°
|
|
cos(lr)[1 - cos(lz)]
l
|
dl - | |
| -
M22(z,r,w)] - |
q
G
|
M22(z,z0,w). | | |
| |
(2.2) |
Рассмотрим
представления (2.1) как сингулярные интегральные уравнения и воспользуемся для
них решениями [8,9]
|
|
|
| s(t,w) = - |
2
p2
|
|
d
dt
|
|
l
у
х
t
|
|
dx
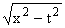 |
|
d
dx
|
|
x
у
х
°
|
|
sFs(s)ds
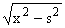 |
| |
|
|
| t(t,w) = |
2
p2t
|
|
d
dt
|
|
l
у
х
t
|
|
xdx
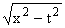 |
|
x
у
х
°
|
|
sFўs (s)ds
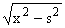 |
+ |
C
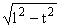 |
, | | |
| |
(2.3) |
где [C/(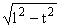 )] - частное тривиальное решение второго сингулярного интегрального уравнения из
(2.1), для случая, когда Fr(s) = 0.
)] - частное тривиальное решение второго сингулярного интегрального уравнения из
(2.1), для случая, когда Fr(s) = 0.
Произведя в
(2.3) интегрирование с учетом значений (2.2), получим систему интегральных
уравнений второго рода
|
| s(t,w) = |
Ґ
у
х
°
|
s(r,w)K11(r,t)dr + |
Ґ
у
х
°
|
t(r,w)K12(r,t)dr + f1(t,w), | |
| t(t,w) = |
Ґ
у
х
°
|
s(r,w)K21(r,t)dr + |
Ґ
у
х
°
|
t(r,w)K22(r,t)dr + f2(t,w), | | |
| |
(2.4) |
где Kij(r,t) -
обозначения, которые содержат коэффициенты Mij.
Система интегральных уравнений (2.4) может быть решена
методом последовательных приближений, если выполняется условие
|
max
j=1,2
|
|
м
н
о |
l
у
х
°
|
|Kj1(r,t)|dt + |
l
у
х
°
|
|Kj2(r,t)|dt |
ь
э
ю |
< 1. | |
(2.5) |
Подстановка t(t,w) из (2.3) в
равенство (1.10) и интегрирование для неизвестного постоянного числа C дает
значение
Институт механики НАН РА
Литература
1. Абрамян Б. Л. Пространственные задачи теории упругости. Ереван. Гитутюн. 1998.
275 с.
2. Achenbach J. D. Wave propagation in Elastic Solids. Amsterdam. North-Holand Publ. Co.
1973. 425 p.
3. Нобль Б. Метод Винера-Хопфа. М. ИЛ. 1962. 279 с.
4. Развитие теории контактных задач
в СССР. Под общей ред. Л. А. Галина. М. Наука.
1976. 493 с.
5. Бабешко В. А. - ПММ. 1969. Т. 33. Вып. I. C. 52-60.
6. Бабешко В. А. - ДАН СССР. 1973. Т. 210. № 6. С.
1310-1313.
7. Бабешко В. А. - ДАН СССР. 1975. Т. 220. № 6. С. 1293-1296.
8.
Ахиезер Н. И., Щербина В. А. - Зап. мат.
отд-ния физ.-мат. фак. ХГУ и Харьк. мат. о-ва. 1957. Т. 25. Сер. 4. С.
191-198.
9. Cooke C. - Glasgow
Math. Journal. 1970. V. 11. № 1. P. 9-22.
![]() = us(r,z)eiwt (s = r,z) -
перемещения;
= us(r,z)eiwt (s = r,z) -
перемещения;
![]() = ss(r,z)eiwt,
= ss(r,z)eiwt,
![]() = trz(r,z)eiwt - напряжения в
цилиндрической системе координат; g - величина
амплитуды колебаний облицовки, которую в условиях (1.1) считаем известной, q -
интенсивность динамической нагрузки, z0 - расстояние приложенной,
осесимметричной динамической нагрузки от облицовки, 2l - ширина облицовки, R -
радиус цилиндрической полости, w - частотный параметр, G - модуль сдвига
упругого пространства.
= trz(r,z)eiwt - напряжения в
цилиндрической системе координат; g - величина
амплитуды колебаний облицовки, которую в условиях (1.1) считаем известной, q -
интенсивность динамической нагрузки, z0 - расстояние приложенной,
осесимметричной динамической нагрузки от облицовки, 2l - ширина облицовки, R -
радиус цилиндрической полости, w - частотный параметр, G - модуль сдвига
упругого пространства.![]() )] - частное тривиальное решение второго сингулярного интегрального уравнения из
(2.1), для случая, когда Fr(s) = 0.
)] - частное тривиальное решение второго сингулярного интегрального уравнения из
(2.1), для случая, когда Fr(s) = 0.