МЕХАНИКА
УДК 539.3
С. О. Саркисян, А. Ж. Фарманян
Условия существования затухающих решений для
тонких
пластин по несимметричной теории упругости
(Представлено академиком С. А. Амбарцумяном 19/XII 2000)
На основе метода сингулярных возмущений [1-3]
в работах [4,5] построен основной (внутренний) итерационный процесс. В работе
[6] изучен вспомогательный итерационный процесс (плоский и антиплоский
погранслои) для тонкой пластинки по несимметричной теории упругости.
Дальнейшее исследование в этом направлении состоит в
изучении сращивания указанных разложений, при котором весьма актуально получение
условий существования затухающих решений от боковой поверхности пластинки по
несимметричной теории упругости при различных вариантах краевых условий. Как и
при симметричной теории упругости [1,2, 7-9], условия существования затухающих
решений в несимметричной теории упругости позволяют разделить решение общего
напряженно-деформированного состояния пластинки на две самостоятельные краевые
задачи: внутреннюю задачу и задачу погранслоя. В данной работе получены общие
условия существования затухающих решений от боковой поверхности пластинки по
несимметричной теории упругости при однородных граничных условиях на лицевых
поверхностях и различных видах трехмерных граничных условий на боковой
поверхности пластинки.
1. Из вариационного уравнения
трехмерной теории несимметричной упругости [10] в качестве уравнений Эйлера и
естественных (эйлеровых) граничных условий следуют уравнения равновесия,
геометрические соотношения, физические соотношения и граничные условия
трехмерной несимметричной теории упругости.
На основе
асимптотической теории тонких пластин [4-6] решение трехмерной проблемы
несимметричной теории упругости состоит из решения внутренней задачи (основного
напряженно-деформированного состояния) и задачи погранслоя (плоского и
антиплоского). Компоненты вектора перемещения, вектора независимого поворота,
компоненты силового и моментного тензоров напряжений представляются в виде
|
м
п
п
н
п
п
о
|
| ui = |
_
ui
|
+ |
p
ui
|
+ |
a
ui
|
, wi = |
_
wi
|
+ |
p
wi
|
+ |
a
wi
|
, | |
| si = si + |
p
si
|
+ |
a
si
|
mij = |
_
mij
|
+ |
p
mij
|
+ |
a
mij
|
| | |
(1) | |
где
индекс (-) относится к внутреннему
напряженно-деформированному состоянию; (p) - к плоскому погранслою; (a) - к
антиплоскому погранслою. Решение внутренней задачи имеет незатухающий характер и
захватывает всю область трехмерной пластинки, а решение задачи погранслоя при
удалении от боковой поверхности пластинки в глубь тела носит быстро затухающий
характер.
При решении краевой задачи несимметричной теории
упругости для изотропной пластинки через решение внутренней задачи [4,5] и
задачи погранслоя [6] удается удовлетворить всем соотношениям трехмерной теории,
за исключением трехмерных граничных условий на боковой поверхности пластинки.
Следовательно, в вариации функционала трехмерной несимметричной теории упругости
остается специально удовлетворить слагаемым, соответствующим граничным условиям
на боковой поверхности S = S1 И S2 пластинки. Принимая во внимание (1), будем
иметь
|
|
у
х
S1
|
|
й
л
|
|
ж
и
|
|
_
sij
|
+ |
p
sij
|
+ |
a
sij
|
|
ц
ш
|
nj - P*i |
щ
ы
|
d |
ж
и
|
|
_
ui
|
+ |
p
ui
|
+ |
a
ui
|
|
ц
ш
|
dS + | |
| + |
у
х
S1
|
|
й
л
|
|
ж
и
|
|
_
mij
|
+ |
p
mij
|
+ |
a
mij
|
|
ц
ш
|
nj - m*i |
щ
ы
|
d |
ж
и
|
|
_
wi
|
+ |
p
wi
|
+ |
a
wi
|
|
ц
ш
|
dS + | |
| + |
у
х
S1
|
|
й
л
|
u*i - |
ж
и
|
|
_
ui
|
+ |
p
ui
|
+ |
a
ui
|
|
ц
ш
|
|
щ
ы
|
d |
ж
и
|
|
_
pi
|
+ |
p
pi
|
+ |
a
pi
|
|
ц
ш
|
dS + | |
| + |
у
х
S1
|
|
й
л
|
w*i - |
ж
и
|
|
_
wi
|
+ |
p
wi
|
+ |
a
wi
|
|
ц
ш
|
|
щ
ы
|
d |
ж
и
|
|
_
mi
|
+ |
p
mi
|
+ |
a
mi
|
|
ц
ш
|
dS =
0. | | |
(2) | |
Здесь на части боковой поверхности S1 заданы силовые и моментные граничные условия, а
на S2 - краевые условия для компонентов
перемещений и поворотов.
Так как по предположению решение
внутренней задачи и решение задачи погранслоя независимы, то выражение (2)
распадается на две самостоятельные задачи. Остановимся на той части выражения
(2), которая относится к внутренней задаче. Будем иметь
|
|
у
х
S1
|
|
й
к
л
|
ж
з
и
|
_
sij
|
+ |
p
sij
|
+ |
a
sij
|
ц
ч
ш
|
nj - P*i |
щ
ъ
ы
|
d |
_
ui
|
dS + |
у
х
S1
|
|
й
к
л
|
ж
з
и
|
_
mij
|
+ |
p
mij
|
+ |
a
mij
|
ц
ч
ш
|
nj - m*i |
щ
ъ
ы
|
d |
_
wi
|
dS + | |
|
у
х
S2
|
|
й
к
л
|
u*i - |
ж
з
и
|
_
ui
|
+ |
p
ui
|
+ |
a
ui
|
ц
ч
ш
|
щ
ъ
ы
|
d |
_
sij
|
njdS + |
у
х
S2
|
|
й
к
л
|
w*i- |
ж
з
и
|
_
wi
|
+ |
p
wi
|
+ |
a
wi
|
ц
ч
ш
|
щ
ъ
ы
|
d |
_
mij
|
dS =
0. | | |
(3) | |
Рассмотрим
теперь два независимых состояния - основное напряженно - деформированное
состояние и погранслой, которые имеют место в пластинке при действии внешних
указанных нагрузок. Для этих независимых напряженно-деформированных состояний
примем теорему о взаимности работ трехмерной несимметричной теории упругости
[10]
|
у
х
v
|
(sijgijў + mijcijў)dv = |
у
х
v
|
(sijўgij + mijўcij)dv. (4) | |
В
результате получим
|
|
у
х
v
|
|
й
к
л
|
_
sij
|
|
ж
з
и
|
p
gij
|
+ |
a
gij
|
ц
ч
ш
|
+ |
_
mij
|
|
ж
з
и
|
p
cij
|
+ |
a
cij
|
ц
ч
ш
|
щ
ъ
ы
|
dv = |
у
х
v
|
|
й
к
л
|
ж
з
и
|
p
sij
|
+ |
a
sij
|
ц
ч
ш
|
|
_
gij
|
+ |
ж
з
и
|
p
mij
|
+ |
a
mij
|
ц
ч
ш
|
|
_
cij
|
щ
ъ
ы
|
dv. | | |
(5) | |
В
выражении (5) независимоe варьированиe допустимo как с силовыми и моментными
напряжениями, так и с перемещениями, независимыми поворотами. Независимость
внутреннего напряженно-деформированного состояния и погранслоя друг от друга и в
этом случае приводит к двум независимым выражениям, одно из которых имеет вид
|
|
у
х
v
|
|
й
к
л
|
ж
з
и
|
p
gij
|
+ |
a
gij
|
ц
ч
ш
|
d |
_
sij
|
+ |
ж
з
и
|
p
cij
|
+ |
a
cij
|
ц
ч
ш
|
d |
_
mij
|
щ
ъ
ы
|
dv = |
у
х
v
|
|
й
к
л
|
ж
з
и
|
p
sij
|
+ |
a
sij
|
ц
ч
ш
|
d |
_
gij
|
+ |
ж
з
и
|
p
mij
|
+ |
a
mij
|
ц
ч
ш
|
d |
_
cij
|
щ
ъ
ы
|
dv. | | |
(6) | |
Трехмерную область v пластинки представим в виде суммы двух областей:
v = v1 И v2, где область
v1 примыкает к боковой поверхности S и
соответствует погранслою, а v2 - внутренняя область, в которой
решение погранслоя равно нулю (т. е. решение погранслоя в
указанной области полностью затухает).
|
| |
ж
з
и
|
p
gij
|
є |
a
gij
|
є
0, |
p
cij
|
є |
a
cij
|
є
0, |
p
sij
|
є |
a
sij
|
є
0, |
p
mij
|
є |
a
mij
|
є
0, |
p
ui
|
є |
a
ui
|
є
0, |
p
wi
|
є |
a
wi
|
є
0 в v2 |
ц
ч
ш
|
| | |
| |
Рассмотрим область v1 границами которой являются боковая
поверхность S = S1 И S2, лицевые поверхности пластинки S+ и
S- и S0.
Здесь S0 - поверхность, перпендикулярная к
срединной плоскости пластинки S, разделяющая трехмерные области
v1 и v2 (т. е. из пластинки
выделяется та часть области v(v1) в виде криволинейного
стержня, в которой имеет место погранслой). Тогда из (6) будем иметь
|
|
у
х
v1
|
|
й
к
л
|
ж
з
и
|
p
gij
|
+ |
a
gij
|
ц
ч
ш
|
d |
_
sij
|
+ |
ж
з
и
|
p
cij
|
+ |
a
cij
|
ц
ч
ш
|
d |
_
mij
|
щ
ъ
ы
|
dv = - |
у
х
v1
|
|
й
к
л
|
ж
з
и
|
p
uj
|
+ |
a
uj
|
ц
ч
ш
|
d |
_
sij,i
|
+ | |
| + |
ж
з
и
|
p
wj
|
+ |
a
wj
|
ц
ч
ш
|
(d |
_
mij,i
|
+ eijkd |
_
sij
|
) |
щ
ъ
ы
|
dv + |
у
х
S2
|
|
й
к
л
|
ж
з
и
|
p
uj
|
+ |
a
uj
|
ц
ч
ш
|
d |
_
sij
|
+ | |
| + |
ж
з
и
|
p
wj
|
+ |
a
wj
|
ц
ч
ш
|
d |
_
mij
|
щ
ъ
ы
|
njdS + |
у
х
S+
|
|
й
к
л
|
ж
з
и
|
p
uj
|
+ |
a
uj
|
ц
ч
ш
|
d |
_
sij
|
+ |
ж
з
и
|
p
wj
|
+ |
a
wj
|
ц
ч
ш
|
d |
_
mij
|
щ
ъ
ы
|
njdS + | |
|
у
х
S-
|
|
й
к
л
|
ж
з
и
|
p
uj
|
+ |
a
uj
|
ц
ч
ш
|
d |
_
sij
|
+ |
ж
з
и
|
p
wj
|
+ |
a
wj
|
ц
ч
ш
|
d |
_
mij
|
щ
ъ
ы
|
njdS + |
у
х
S0
|
|
й
к
л
|
ж
з
и
|
p
uj
|
+ |
a
uj
|
ц
ч
ш
|
d |
_
sij
|
+ |
ж
з
и
|
p
wj
|
+ |
a
wj
|
ц
ч
ш
|
d |
_
mij
|
щ
ъ
ы
|
njdS. | | |
| |
Вариации компонент силовых и моментных напряжений
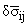 и
и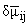 будем выбирать
таким образом, чтобы они удовлетворяли однородным уравнениям равновесия и
однородным граничным условиям на лицевых поверхностях пластинки S+ и
S-. Тогда первый, третий, четвертый
интегралы в выражении (7) будут равны нулю. Пятый интеграл в (7) тоже равен
нулю, в силу затухания величин погранслоя. В итоге получим
будем выбирать
таким образом, чтобы они удовлетворяли однородным уравнениям равновесия и
однородным граничным условиям на лицевых поверхностях пластинки S+ и
S-. Тогда первый, третий, четвертый
интегралы в выражении (7) будут равны нулю. Пятый интеграл в (7) тоже равен
нулю, в силу затухания величин погранслоя. В итоге получим
|
|
у
х
v1
|
|
й
к
л
|
ж
з
и
|
p
gij
|
+ |
a
gij
|
ц
ч
ш
|
d |
_
sij
|
+ |
ж
з
и
|
p
cij
|
+ |
a
cij
|
ц
ч
ш
|
d |
_
mij
|
щ
ъ
ы
|
dv = |
у
х
S2
|
|
й
к
л
|
ж
з
и
|
p
uj
|
+ |
a
uj
|
ц
ч
ш
|
d |
_
sij
|
+ |
ж
з
и
|
p
wj
|
+ |
a
wj
|
ц
ч
ш
|
d |
_
mij
|
) |
щ
ъ
ы
|
nidS. | | |
(8) | |
Таким
же образом будем иметь
|
|
у
х
v1
|
|
й
к
л
|
ж
з
и
|
p
sij
|
+ |
a
sij
|
ц
ч
ш
|
d |
_
gij
|
+ |
ж
з
и
|
p
mij
|
+ |
a
mij
|
ц
ч
ш
|
d |
_
cij
|
щ
ъ
ы
|
dv = |
у
х
S1
|
|
й
к
л
|
ж
з
и
|
p
sij
|
+ |
a
sij
|
ц
ч
ш
|
d |
_
uj
|
+ |
ж
з
и
|
p
mij
|
+ |
a
mij
|
ц
ч
ш
|
d |
_
wj
|
щ
ъ
ы
|
nidS. | | |
(9) | |
В
результате при помoщи (6), (8) и (9) получим
|
|
у
х
S2
|
|
й
к
л
|
ж
з
и
|
p
uj
|
+ |
a
uj
|
ц
ч
ш
|
d |
_
sij
|
+ |
ж
з
и
|
p
wj
|
+ |
a
wj
|
ц
ч
ш
|
d |
_
mij
|
щ
ъ
ы
|
nidS = |
у
х
S1
|
|
й
к
л
|
ж
з
и
|
p
sij
|
+ |
a
sij
|
ц
ч
ш
|
d |
_
uj
|
+ |
ж
з
и
|
p
mij
|
+ |
a
mij
|
ц
ч
ш
|
d |
_
wj
|
щ
ъ
ы
|
nidS. | | |
(10) | |
На
основе (10) из (3) окончательно получим
|
у
х
S1
|
[( |
_
sij
|
nj - p*i)d |
_
ui
|
+ ( |
_
mij
|
nj - m*i)d |
_
wi
|
]dS + |
у
х
S2
|
[(u*i- |
_
ui
|
)d |
_
sij
|
nj + (w*i - |
_
wi
|
)d |
_
mij
|
nj]dS =
0. (11) | |
Итак,
в виде формулы (11) выделена та часть вариационного соотношения, которая
полностью относится к внутреннему (основному) напряженно-деформированному
состоянию. В этом и состоит ее ценность.
При исследовании
внутренней задачи [4,5] асимптотический анализ приводит к определенным
качественным распределениям по координате x3 величин поставленной
задачи. Если в формулу (11) вместо величин внутренней задачи подставить
указанные результаты, получим характерные для внутренней задачи краевые условия,
качественныe в смысле удовлетворения общим трехмерным краевым условиям по
несимметричной теории упругости, подставленным на боковой поверхности пластинки.
Эта закономерность определяет также качественную сторону краевых условий,
которые соответствуют погранслою. Качественную сторону граничных условий
погранслоя называют условиями существования затухающих решений от боковой
поверхности пластинки или условиями согласованности при распределении общих
трехмерных краевых условий по несимметричной теории упругости между внутренней
задачей и задачей погранслоя.
Допустим, что на боковой
поверхности пластинки заданы силовые и моментные трехмерные краевые условия (в
таком случае в формуле (11) исчезает второй интеграл по поверхности S2). Считаем, что контур срединной плоскости
пластинки совпадает с координатной линией a2
В случае симметричной по
x3 задачи в асимптотическом смысле главные члены в нулевом
приближении выражаются формулами:
| s11 = s11(a1,a2), s12 = s12(a1,a2), s21 = s21(a1,a2), s22 = s22(a1,a2), (12) | |
| m13 = m13(a1,a2),
u1 = u1(a1,a2),
u2 = u2(a1,a2),
w3 = w3(a1,a2), | |
а
в случае кососимметричной по x3 задачи:
|
| s13 = s13(a1,a2), s23 = s23(a1,a2), m11 = m11(a1,a2), m12 = m12(a1,a2), | |
| m22 = m22(a1,a2),
w1 = w1(a1,a2),
w2 = w2(a1,a2), u3 = u3(a1,a2). | | |
(13) | |
Подставляя
(12) или (13) в выражение (11), получим краевые условия внутренней задачи в
каждой точке контура в срединной плоскости пластинки:
для
симметричной задачи
| T11/a1=a10 = |
h
у
х
-h
|
p*1dx3,
S12/a1=a10 = |
h
у
х
-h
|
p*2dx3,
L13/a1=a10 = |
h
у
х
-h
|
m*3dx3, (14) | |
для
кососимметричной задачи
| L11/a1=a10 = |
h
у
х
-h
|
m*1dx3,
L12/a1=a10 = |
h
у
х
-h
|
m*2dx3,
N13/a1=a10 = |
h
у
х
-h
|
p*3dx3. (15) | |
Формулы
(14) и (15) не только определяют краевые условия на контуре l срединной
плоскости пластинки для внутренней задачи в исходном асимптотическом приближении
(для симметричной и кососимметричной по x3 задач соответственно), но
одновременно указывают, что погранслой в исходном асимптотическом приближении на
каждом нормальном сечении на контуре l срединной плоскости пластинки будет
удовлетворять самоуравновешенным по толщине пластинки силовым и моментным
краевым условиям.
Разработанный подход позволяет
аналогичным образом рассматривать и другие виды трехмерных краевых условий по
несимметричной теории упругости на боковой поверхности пластинки.
Гюмрийский
государственный
педагогический институт им. М. Налбандяна
Литература
1. Гольденвейзер А.Л. Теории упругих тонких оболочек. М. Наука. 1976.
510 с.
2. Агаловян Л.А. Асимптотическая теория анизотропных пластин и оболочек. М. Наука. 1997.
414 с.
3. Саркисян С.О. Общая двумерная теория магнитоупругости тонких оболочек. Ереван. Изд-во
АН Армении. 1992.
4. Саркисян С.О. -
ДНАН Армении. 1999. T. 99. № 2. С.
138-147.
5. Саркисян С.О. - ДНАН Армении. Т. 99, № 3. С. 216-225.
6. Саркисян С.О., Фарманян А. Ж. Матер. Междунар. конф.
"Прикладные и математические аспекты естествознания". Ереван; 1999. Ноян-Тапан.
1999. С. 51-55.
7. Гусейн-Заде М.И. - ПММ. 1965. Т. 29. С. 752-795.
8. Агаловян Л.А., Хачатрян Ш.М. - ДАН АрмССР. 1975. Т. 50. №
3. С. 157-163.
9. Бутенко Ю.И. В сб.: Исследования по теории пластин и оболочек. Казань. Изд-во КГУ.
1990. С. 15-25.
10. Новацкий В. - Теория упругости. М. Мир. 1975. 872 с.
![]() и
и![]() будем выбирать
таким образом, чтобы они удовлетворяли однородным уравнениям равновесия и
однородным граничным условиям на лицевых поверхностях пластинки S+ и
S-. Тогда первый, третий, четвертый
интегралы в выражении (7) будут равны нулю. Пятый интеграл в (7) тоже равен
нулю, в силу затухания величин погранслоя. В итоге получим
будем выбирать
таким образом, чтобы они удовлетворяли однородным уравнениям равновесия и
однородным граничным условиям на лицевых поверхностях пластинки S+ и
S-. Тогда первый, третий, четвертый
интегралы в выражении (7) будут равны нулю. Пятый интеграл в (7) тоже равен
нулю, в силу затухания величин погранслоя. В итоге получим