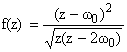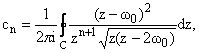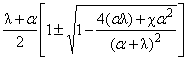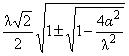МЕХАНИКА
УДК 393.3.
Д. М. Минасян, М. М. Минасян
Новое приближение в задаче
о флаттере пластинки в
сверхзвуковом потоке газа
(Представлено академиком В. С. Саркисяном 18/X 2000)
Задача обтекания деформируемых тел потоком
жидкости и газа в строгой постановке требует совместного рассмотрения систем
уравнений обеих сред с соблюдением условий их контакта. Очевидно, что это
обстоятельство порождает новые сложности, помимо тех, которые присущи каждой
средe в отдельности. В случае безграничных сред в линейной постановке задачи
методом элементарных решений можно исследовать дисперсионное уравнение и
получить точные оценки для границ устойчивости флаттерных колебаний обтекаемых
тел. Однако для конечных тел, особенно в задачах с начальными и граничными
условиями, общее исследование динамического поведения тел связано с
непреодолимыми трудностями.
Одна из возможностей
частичного преодоления таких трудностей заключается в установлении
дифференциальных уравнений для движения тел. Примером может служить известная
"поршневая" теория [1]. Однако эта теория, весьма эффективная при больших
сверхзвуковых скоростях обтекания, при умеренных скоростях просто не применима,
не говоря о том, что она не позволяет удовлетворить всем возможным граничным и
начальным условиям. В данной работе строится новое приближение, которое
позволяет устранить эти и некоторые другие недостатки "поршневой" теории.
1. Рассмотрим обтекание бесконечной пластинки двумерным
сверх-звуковым потоком идеального газа. При одностороннем обтекании, решая
линеаризированную задачу движения газа, для изображения давления p(w,k) (преобразования по Лапласу и Фурье), получается [1,2]
|
| p(w,k) = ir0a0 |
(w - Uk)2
m(w,k)
|
w(w,k), | |
| m(w,k) = |
Ц
|
(w - Uk)2 - a20k2
|
, Imm <
0, | | |
(1) | |
где
w(w,k) - изображение прогиба (цилиндрического по форме)
пластинки, r0,a0,U - известные
параметры невозмущенного потока газа. Из (1) для оригинала по Фурье получается
интегральное соотношение Вольтеррова типа с ядром [1]
| K(x - x) = exp |
м
н
о |
- |
iMw(x - x)
a0(M2 - 1)
|
ь
э
ю |
J0 |
й
к
л |
w(x - x)
a0(M2 - 1)
|
щ
ъ
ы |
, M = |
U
a0
|
> 1. (2)
| |
Учитывая
теорему сложения для функций Бесселя
| J0(x - y) = J0(x)J0(y) + 2 |
Ґ
е
m=1
|
Jm(x)Jm(y), (3) | |
в
принципе связь между p(x,t) и w(x,t) можно представить дифференциальным
соотношением, поскольку каждое слагаемое ряда (3) с экспонентой в (2)
представляет вырожденное ядро. Однако следует ожидать, что в итоге получится
уравнение высокого порядка и с переменными коэффициентами. Этот путь следует
считать неэффективным.
Другой подход для сведения
интегральной связи к дифференциальной связан с разложением функций (w - Uk)2/m на рациональные слагаемые. На этом пути «нулевому»
приближению будет соответствовать «поршневое» приближение, которое получается
заменой m(w,k) на U - wk. Для построения следующего
приближения воспользуемся идеей построения приближенной модели нелокальной
упругой среды [3], когда комплексный оператор ядра упругой энергии
аппроксимируется полиномом по первым корням ядра. Здесь эта идея подсказывает
аппроксимацию комплексного ядра конечным отрезком ряда Лорана по первым
особенностям. Как видно из (1), особенность этого ядра суть точки ветвления
w = (U ± a0)k в
комплексной плоскости w. Выбрав меньшую по модулю
особую точку w0 = (U - a0)k и введя замену z = w - a0k, разложим функцию
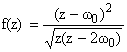 (4) (4) | |
по
степеням z. Отметим, что функция f(z) аналитична в области 2|w0| < |z|
< +Ґ. Для коэффициентов ряда Лорана имеем
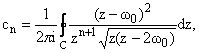 (5) (5) | |
где
контур C охватывает разрез [0;2w0].
Единственной особой
точке подынтегральных функций вне контура C соответствует простой полюс в точке
z = Ґ. Применив инверсию x =
w0z-1 и
разложив в ряд Тейлора, для коэффициентов cn получим
| cn = |
w0n-1
2pi
|
|
у
х
C
|
(1 - x)2 |
Ґ
е
m=0
|
|
(2m - 1)!!
m!
|
xm+n-2dx, cn = 0, n
і
2. (6) | |
Ограничиваясь
только тремя членами ряда, для давления p(w,k) вместо
(1) теперь будем иметь
| p(w,k) = ir0a0 |
й
к
л |
w - Uk + |
a20k2
w - (U - a0)k
|
щ
ъ
ы |
w(w,k). (7) | |
В
оригиналах из (7) получим
|
D1p
Dt
|
= r0a0 |
D1
Dt
|
|
ж
з
и |
Dw
Dt
|
ц
ч
ш |
+ |
r0a30
2
|
|
¶2w
¶x2
|
, (8) | |
где
|
D1
Dt
|
= |
¶
¶t
|
+ (U - a0) |
¶
¶x
|
, |
D
Dt
|
= |
¶
¶t
|
+ U |
¶
¶x
|
. | |
В
работе [4] уравнение (8) выведено методом последовательных приближений, однако
этот подход привел к тому, что вместо оператора D1 в левой части (8)
оказался оператор D. Это отличие объясняется именно тем, что в [4] не было
соблюдено правило сохранения особенностей, и, как это часто бывает, все
дальнейшие приближения не устраняют этот дефект.
Удержание
последующих членов ряда Лорана, повышая порядок дифференциальной связи p ~ w, не будет иметь особого смысла и не может описывать
качественно новые эффекты. Однако для учета влияния отброшенной части этого ряда
половинный коэффициент при последнем члене (8) будем заменять не определенным
пока коэффициентом c.
2. В
качестве примера для иллюстрации эффективности предложенного приближения
рассмотрим задачу, допускающую точный анализ и при (1), и при (7). В задаче об
обтекании бесконечной пластинки имеем систему (в обозначениях [1])
|
м
п
н
п
о |
|
|
| L[w] = rh |
ж
з
и
|
¶2w
¶t2
|
+ e |
¶w
¶t
|
ц
ч
ш
|
+ D |
¶4w
¶x4
|
- Nx |
¶2w
¶x2
|
+ kfw. | | |
(9) | |
Исключив
давление, получим уравнение для прогиба
|
D1
Dt
|
|
й
к
л |
L[w] + r0a0 |
Dw
Dt
|
щ
ъ
ы |
+ cr0a30 |
¶2w
¶x2
|
= 0. (10) | |
Представив
решение в виде бегущих волн
| w(x,t) = w0exp[i(wt - kx)], (11) | |
из
(10) получим дисперсионное уравнение
| [w - (U - a0)k][w2 - c2k2 - igw + ie0Uk] - idk2 = 0, (12) | |
где
введены обозначения
| c2 = |
D
ph
|
k2 + |
Nx
ph
|
+ |
kf
k2
|
, e0 = |
r0a0
ph,
|
, g =
e + e0, d = ce0a20. (13) | |
Для
устойчивости волн все корни уравнения (13) должны находиться в верхней
полуплоскости комплексной плоскости w. По известным
критериям Раусса - Гурвица [5] число корней, находящихся в нижней полуплоскости,
равно числу перемен знаков в ряду
| 1;g;k2[(g2c2 - e20U2) + dg]; dk6[c2(e0U + (U - a0)g)2 - (e0U(U - a0) + gc2 + d)2]. (14) | |
Тогда
область устойчивости определится системой неравенств
|
м
н
о |
|
|
| c[Ue0 + (U - a0)g] > e0U(U - a0) + gc2 + d. | | |
(15) | |
Из
этой системы для границы устойчивости получим уравнение
| [U - (c + a0)][Ue0 - gc] + d =
0. (16) | |
Введя
новые обозначения
| f = |
U
c
|
, l =
|
e
e0
|
, a =
|
a0
c
|
, g =
1 + l, (17) | |
из
(16) для функции f(l,a)
получим
f(l,a) = 1 +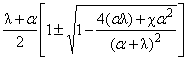 (18)
(18) |
|
Сравним
эту функцию с аналогичной функцией, полученной на основе (1). Она приведена в
работе [2] и в обозначениях, принятых в настоящей работе, имеет вид
fT(l,a) = 1 +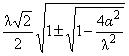 (19)
(19) |
|
На
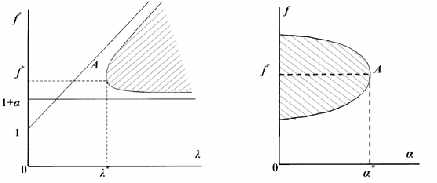
рис.1 схематично представлена функция f(l) при
постоянном a, а на рис.2 - функция f(a) при постоянном l. Графики
соответствующих функций из (19) качественно такие же. У функций f(l) и fT(l) одни и те же
наклонная - f = 1 + l и горизонтальная - f = 1 + a асимптоты. Отметим, что по «поршневой» теории областью
устойчивости является вся область ниже линии f = 1 + l, а
по приближению работы [4] горизонтальная асимптота смещена вниз на линию f = 1.
Выбрав значение 0.25 для поправочного коэффициента c, в
(18) для точек ветвлений на рис. 1 получим
l* = l*T = 2a, f* = 1 + 1.5a, f*T = 1 + a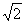 , (20) , (20) | |
а
для точек ветвлений на рис. 2 получим
| a* = a*T = 0.5l, f* = 1 + 0.75l, f*T = 1 + 0.71l. (21) | |
Рис.
1. Рис.
2.
3. Подведем итоги. Итак, вместо "поршневого" приближения,
которое имеет локальный характер зависимости аэродинамического давления от
геометрии движения пластинки, предлагается нелокальная дифференциальная связь
(8). Если отбросить последний член в этой связи, то вернемся к "поршню". В этом
смысле предложенное здесь приближение можно считать обобщением "поршневого"
приближения. Однако следует отметить, что это обобщение носит определяющий
характер, если рассматривать его по принципу сохранения основных качественных
особенностей задачи в "точной" постановке. Сказанное проиллюстрируем на примере
бесконечной пластинки, разобранном выше.
Дисперсионное
уравнение для системы (9), как при (1), так и при (8), имеет три ветви решения
w(k), в то время как по "поршневой" теории имеются
только две ветви, что приводит к потере одного корня в комплексной плоскости
w. Как уже было сказано, вся область ниже наклонной
асимптоты на рис. 1 по "поршневой" теории является областью устойчивости.
Очевидно, что переход именно третьего корня через действительную ось плоскости
w порождает нижнюю границу флаттера.
Как видно из рис.1, существует нижний порог
конструкционного демпфирования l* для парирования флаттера, в противовес "поршневой"
теории.
Важной отличительной чертой предложенного
приближения является повышение порядка (на единицу) уравнения движения пластинки
по сравнению с "поршневым" приближением. Это позволит учитывать начальное
значение давления на пластинку и условие сверхзвукой кромки для конечной
пластинки в смешаной задаче обтекания.
Ереванский государственный университет
Литература
1. Болотин В. В. Неконсервативные задачи теории упругой устойчивости. М. Физматгиз. 1961.
339 с.
2. Kornecki A. - II SM
Archives. 1979. V. 4, Issue 4. P. 241-343.
3. Кунин И. А. Теория упругих сред с микроструктурой. М.
Наука. 1975. 415 с.
4. Белубекян М. В.,
Минасян М. М. - Механика. Изв. НАН Армении. 1997. Т. 50. № 2. С.
27-35.
5. Гантмахер Ф. Р. - Теория матриц. М. Наука. 1967. 575 с.